Công thức tính Chu vi và Diện tích hình tròn Cách tính chu vi hình tròn, diện tích hình tròn
Công thức tính chu vi hình tròn, diện tích hình tròn được áp dụng rất nhiều trong quá trình học tập cũng như trong cuộc sống hàng ngày. Trước tiên, bạn cần hiểu hình tròn là gì? Hình tròn là hình gồm các điểm nằm trên hình tròn và các điểm nằm bên trong đường tròn đó.
Công thức tính chu vi, diện tích hình tròn
Diện tích hình tròn
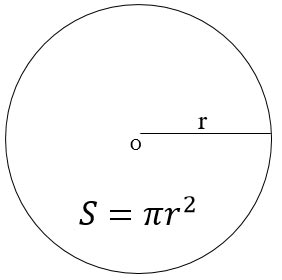
Diện tích hình tròn được tính theo bằng bình phương bán kính hình tròn x PI:
\(S\ =\ r\ \times r\ \times\pi\ \left(pi\right)\)
hoặc\(S=\frac{d\ \times\ d}{4}\times\pi\ \left(pi\right)\)
Trong đó:
- S: Là diện tích hình tròn.
- R: Là bán kính hình tròn.
- D: Là đường kính hình tròn.
- \(\pi\): là hằng số giá trị tương đương 3.14.
Chu vi hình tròn
Chu vi hình tròn hay còn gọi là độ dài đường tròn hiểu đơn giản chính là phần đường biên giới hạn của hình tròn. Chu vi hình tròn được tính theo công thức đường kính x PI hoặc 2 lần bán kính x PI.
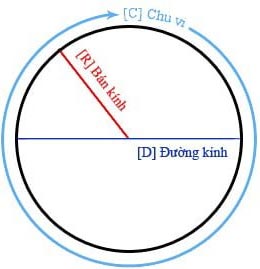
Chu vi hình tròn:
\(\ C\ =\ d\ \times\ \pi\ \left(pi\right)\)
hoặc\(\ C=\ r\ \times2\ \times\pi\ \left(pi\right)\)
Trong đó:
- C: Là chu vi hình tròn.
- R: Là bán kính hình tròn.
- D: Là đường kính hình tròn.
- \(\pi\): Là hằng số giá trị tương đương 3.14.
Ngoài công thức tính chu vi, diện tích cho hình tròn ra bạn còn có thể tham khảo thêm công thức cho hình thoi, hình thang, hình chữ nhật... để áp dụng trong học tập, công việc hiệu quả.
Tìm đường kính, bán kính khi biết chu vi, diện tích hình tròn
Tính đường kính hình tròn
\(d=\frac{C}{\pi}\)
\(d=\sqrt{\frac{S}{\pi}}\ \times2\)
Trong đó:
- d: Đường kính hình tròn
- C: Chu vi hình tròn
- S: Diện tích hình tròn
- \(\pi\): Là hằng số giá trị tương đương 3.14.
Tính bán kính hình tròn
\(r=\frac{C}{2\ \times\pi}\)
\(r=\sqrt{\frac{S}{\pi}}\)
\(r=\frac{d}{2}\)
Trong đó:
- r: Bán kính hình tròn
- d: Đường kính hình tròn
- C: Chu vi hình tròn
- S: Diện tích hình tròn
- \(\pi\): Là hằng số giá trị tương đương 3.14.
So sánh hình tròn với hình vuông
Hình tròn chiếm khoảng 80% diện tích của hình vuông có bề rộng (đường kính) bằng nhau. Giá trị thực tế là (π/4) = 0.785398... = 78.5398...%
Tại sao lại như vậy? Bởi diện tích hình vuông là w2 và diện tích hình tròn là (π/4) × w2
Ví dụ: So sánh hình vuông với hình tròn có đường kính 3m
Diện tích hình vuông = w2 = 32 = 9m2
Ước tính diện tích hình tròn = 80% diện tích hình vuông = 80% : 9 = 7.2m2
Diện tích thực sự của hình tròn = (π/4) × D2 = (π/4) × 32 = 7.07m2 (tới 2 số thập phân).
Ước tính 7.2m2 không chênh quá nhiều so với 7.07m2
Một ví dụ thực tế
Max đang xây một ngôi nhà. Trước hết, anh ấy cần khoan lỗ và lấp đầy bê tông vào chúng. Các lỗ này có chiều rộng 0.4m, độ sâu 1m.Hỏi Max cần đổ bao nhiêu bê tông vào mỗi lỗ?
Cách giải như sau:
Các lỗ có hình tròn (ở mặt cắt ngang) bởi chúng được đục bằng máy khoan.
Với đường kính 0.4m, diện tích của hình là:
A = (π/4) × D2
A = (3.14159.../4) × 0.42
A = 0.7854... × 0.16
A = 0.126m2
Lỗ có độ sâu 1m nên thể tích của nó là:
Thể tích = 0.126m2 × 1 m = 0.126m3
Kết luận, Max cần đổ 0.126m3 bê tông vào mỗi lỗ.
Lưu ý: Max có thể ước tính diện tích bằng cách:
- Tính diện tích một lỗ hình vuông: 0.4 × 0.4 = 0.16m2
- Hình tròn chiếm 80% diện tích hình vuông nên ta có kết quả: 80% × 0.16m2 = 0.128m2
- Thể tích lỗ sâu 1m là: 0.128m3
Trịnh Thị Lương Link Download chính thức:
Lớp 1 
Lớp 2 
Lớp 3 
Lớp 4 
Lớp 5 
Thi vào 6 
Lớp 6 
Lớp 7 
Lớp 8 
Lớp 9 Có thể bạn quan tâm
-
Giáo án Toán lớp 1 (Sách mới) - Giáo án Toán lớp 1 (trọn bộ 5 sách)
-
Tuyển tập đề thi học sinh giỏi môn Toán lớp 3
-
Thuyết minh về Thành Cổ Loa (2 Dàn ý + 5 mẫu)
-
Bộ tranh tô màu chủ đề gia đình cho bé
-
Văn mẫu lớp 10: Phân tích tác phẩm Hiền tài là nguyên khí của quốc gia (2 Dàn ý + 10 Mẫu)
-
Những vần thơ hay - Tuyển tập những bài thơ hay
-
Văn mẫu lớp 9: Nghị luận về hiện tượng học tủ, học vẹt
-
File luyện viết chữ in hoa - Mẫu chữ hoa cho học sinh Tiểu học
-
Đề kiểm tra học kì II môn Toán lớp 1
-
Văn mẫu lớp 7: Phân tích bài Ngẫu nhiên viết nhân buổi mới về quê
