Công thức tính chu vi hình vuông, diện tích hình vuông Cách tính chu vi, diện tích hình hình vuông và một số bài tập ví dụ
Hình vuông là một hình tứ giác, có 4 góc vuông và 4 cạnh có chiều dài bằng nhau. Hình chữ vuông là một trường hợp đặc biệt của hình chữ nhật và có đường chéo vuông góc tại trung điểm.
Bên cạnh hình tam giác, hình vuông cũng là một trong những hình phổ biến nhất trong thực tế khi tính diện tính như tính diện tích nhà cửa, đồ vật, đất đai. Vậy mời các bạn cùng tham khảo công thức tính diện tích, chu vi hình vuông trong bài viết dưới đây:
Công thức Tính chu vi, diện tích hình vuông
Các công thức tính của hình vuông
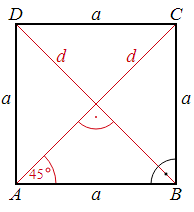
| ⇒ | ||
| ⇒ | ||
| ⇒ |  \(a\ =\ \frac{d}{\sqrt{2}}\) \(a\ =\ \frac{d}{\sqrt{2}}\) |
Trong đó:
|
|
Hình vuông là trường hợp đặc biệt của hình chữ nhật, cũng có 4 góc vuông, đường chéo vuông góc tại trung điểm, 2 cặp cạnh đối song song với nhau. Vậy nên bạn có thể tham khảo công thức tính chu vi, diện tính hình vuông như sau:
Diện tích hình vuông
Công thức tính diện tích hình vuông bằng bình phương chiều dài cạnh hình vuông:
![]() \(S=a^2\)
\(S=a^2\)
Mở rộng: Khi biết diện tích hình vuông, ta có thể tìm cạnh hình vuông bằng công thức:
![]() \(a\ =\ \sqrt{S}\)
\(a\ =\ \sqrt{S}\)
Chu vi hình vuông
Chu vi hình vuông là tổng độ dài các cạnh bao quanh nó. Vì hình vuông có 4 cạnh bằng nhau nên việc tìm chu vi của nó rất đơn giản, bạn chỉ cần tính như sau:
Chu vi hình vuông bằng tổng độ dài 4 cạnh hay gấp 4 lần độ dài của 1 cạnh.
![]() \(C\ =\ 4\ \times a\)
\(C\ =\ 4\ \times a\)
Mở rộng: Khi biết chu vi của hình vuông, ta có thể tìm cạnh hình vuông bằng công thức:
![]() \(a\ =\ C\ :\ 4\)
\(a\ =\ C\ :\ 4\)
Công thức tính đường chéo hình vuông
Như đã nói ở trên, đường chéo của hình vuông có độ dài bằng nhau và có thể tính được thông qua độ dài của cạnh hình vuông, công thức tính độ dài đường chéo hình vuông như sau:
![]() \(d\ =\ \sqrt{a^2\ +\ a^2}=a\sqrt{2}\)
\(d\ =\ \sqrt{a^2\ +\ a^2}=a\sqrt{2}\)
Từ công thức trên, nếu ta đã biết độ dài đường chéo thì có thể tính được cạnh hình vuông theo công thức sau:
 \(a\ =\ \frac{d}{\sqrt{2}}\)
\(a\ =\ \frac{d}{\sqrt{2}}\)
Một số bài toán điển hình về hình vuông
Tính chu vi khi biết diện tích
Biết diện tích của một hình vuông là 25cm2, hãy tính chu vi của hình vuông đó. Các bước cần làm như sau:
- Bước 1: Tính độ dài 1 cạnh:
 \(a\ =\ \sqrt{25}=\ 5cm\)
\(a\ =\ \sqrt{25}=\ 5cm\) - Bước 2: Chu vi hình vuông đó là:
 \(C\ =\ 4\cdot5\ =\ 20cm\)
\(C\ =\ 4\cdot5\ =\ 20cm\)
Tính diện tích khi biết chu vi
Cũng với hình vuông trên, nếu chu vi của hình vuông là 20cm, hãy tính diện tích của hình vuông đó. Các bước cần làm như sau:
- Bước 1: Tính độ dài 1 cạnh:
 \(a\ =\ \frac{20}{4}\ =\ 5cm\)
\(a\ =\ \frac{20}{4}\ =\ 5cm\) - Bước 2: Diện tích hình vuông đó là:
 \(S\ =\ 5\cdot5\ =\ 25cm^2\)
\(S\ =\ 5\cdot5\ =\ 25cm^2\)
Tính diện tích, chu vi khi biết độ dài đường chéo
Cho một hình vuông có độ dài đường chéo là 10cm, hãy tìm chu vi và diện tích của hình vuông đó. Các bước cần làm như sau:
- Bước 1: Tính độ dài cạnh hình vuông:
 \(a\ =\ \frac{10}{\sqrt{2}}\ =7,071067812cm\) (số lẻ thập phân bạn có thể lấy ít hơn)
\(a\ =\ \frac{10}{\sqrt{2}}\ =7,071067812cm\) (số lẻ thập phân bạn có thể lấy ít hơn) - Bước 2: Chu vi của hình vuông là:
 \(C\ =\ 7,071067812\ \times4\ =28,28427125cm\)
\(C\ =\ 7,071067812\ \times4\ =28,28427125cm\) - Bước 3: Diện tích của hình vuông là:
 \(S\ =\ 7,071067812\ \times7,071067812\ =\ 50cm^2\)
\(S\ =\ 7,071067812\ \times7,071067812\ =\ 50cm^2\)
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:
-
 Minh NgọcThích · Phản hồi · 0 · 01/11/22
Minh NgọcThích · Phản hồi · 0 · 01/11/22












 Lớp 2
Lớp 2
 Lớp 4
Lớp 4
 Lớp 5
Lớp 5
 Thi vào 6
Thi vào 6
 Lớp 6
Lớp 6
 Lớp 7
Lớp 7
 Lớp 9
Lớp 9









