Công thức tính Chu vi, Diện tích hình thang Cách tính Chu vi (P), Diện tích (S) hình thang
Hình thang là một hình tứ giác có hai cạnh đáy song song và tổng số đo của các góc bằng 360 độ. Có 3 loại hình thang đó là: hình thang thường, hình thang vuông, hình thang cân.
Hôm nay, chúng tôi xin mời tất cả các bạn cùng tham khảo tài liệu tổng hợp cách tính chu vi, diện tích các loại hình thang.
Công thức tính chu vi, diện tích hình thang
Phân loại hình thang
- Hình thang thường: là hình tứ giác có hai cạnh đáy song song và tổng số đo của các góc bằng 360 độ.

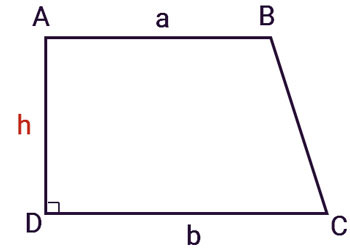
- Hình thang vuông: hình thang có một góc vuông.
- Hình thang cân: là hình thang có hai góc kề một đáy bằng nhau, hoặc độ dài hai cạnh bên bằng nhau.
Công thức tính chu vi hình thang
1. Công thức tính chu vi hình thang thường
Công thức tính chu vi hình thang sẽ là tổng số đo của 4 cạnh của hình thang đó:
![]() \(P=a\ +\ b+c+\ d\)
\(P=a\ +\ b+c+\ d\)
Trong đó:
+ a,c: độ dài hai cạnh đáy.
+ b,d: độ dài hai cạnh bên.
2. Công thức tính chu vi hình thang vuông
Cũng giống với hình thang thường, công thức tính chu vi của hình thang vuông là:
![]() \(P=\ a\ +\ b+\ c\ +d\)
\(P=\ a\ +\ b+\ c\ +d\)
Trong đó:
+ a,c: độ dài hai cạnh đáy.
+ b,d: độ dài hai cạnh bên.
3. Công thức tính chu vi hình thang cân
Khác với hai loại hình thang trên, công thức tính chu vi của hình thang cân sẽ là:
![]() \(P=\ \left(2\ \times a\right)\ +b\ +c\)
\(P=\ \left(2\ \times a\right)\ +b\ +c\)
Trong đó:
+ a: là độ dài của 1 cạnh bên.
+ b,c: là độ dài của hai cạnh đáy.
Công thức tính diện tích hình thang
1. Công thức tính diện tích hình thang thường
Cho hình thang ABCD, có các cạnh: AB = a, DC = b và đường cao AH = h. Công thức tính diện tích của hình thang thường sẽ là:

![]() \(S=h\times\left(\frac{a+b}{2}\right)\)
\(S=h\times\left(\frac{a+b}{2}\right)\)
2. Công thức tính diện tích hình thang vuông
Cho tam giác vuông ABCD, có cạnh AB= a, DC= b, AD= h. Vì vậy, công thức tính của hình thang vuông là:

![]() \(S=\ h\times\left(\frac{a+b}{2}\right)\)
\(S=\ h\times\left(\frac{a+b}{2}\right)\)
3. Công thức tính diện tích hình thang cân
Ngoài việc áp dụng công thức như tính hình thang bình thường, bạn cũng có thể chia nhỏ hình thang cân ra để tính diện tích từng phần rồi cộng lại với nhau.
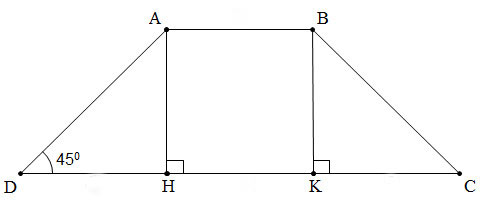
Giả dụ, hình thang cân ABCD có 2 cạnh bên AD và BC bằng nhau. Đường cao AH và BK, hình thang sẽ được chia ra thành 1 hình chữ nhật ABKH và 2 hình tam giác là ADH và BCK. Áp dụng công thức tính diện tích hình chữ nhật cho ABHK và diện tích tam giác cho ADH và BCK sau đó cộng tất cả diện tích để tìm diện tích hình thang ABCD.

Cụ thể thế này:
![]() \(S_{ABCD}=S_{ABKH}+\ S_{ADH}+S_{BCK}\)
\(S_{ABCD}=S_{ABKH}+\ S_{ADH}+S_{BCK}\)
Mà SADH = SBCK (dễ dàng chững minh), ta được:
![]() \(S_{ABCD}\ =\ S_{ABKH}+\left(2\ \times S_{ADH}\right)\)
\(S_{ABCD}\ =\ S_{ABKH}+\left(2\ \times S_{ADH}\right)\)
![]() \(S_{ABCD\ }=\ AB.AH\ \ +\ 2.\ \frac{AH.DH}{2}\ =\ AB.AH\ \ +\ AD.\ AH\ =AH\ .\ \left(AB\ +AD\right)\)
\(S_{ABCD\ }=\ AB.AH\ \ +\ 2.\ \frac{AH.DH}{2}\ =\ AB.AH\ \ +\ AD.\ AH\ =AH\ .\ \left(AB\ +AD\right)\)
Chọn file cần tải:
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:












 Lớp 2
Lớp 2
 Lớp 4
Lớp 4
 Lớp 5
Lớp 5
 Thi vào 6
Thi vào 6
 Lớp 6
Lớp 6
 Lớp 7
Lớp 7
 Lớp 9
Lớp 9









