Chuyên đề vectơ trong không gian, quan hệ vuông góc Tài liệu ôn tập môn Toán lớp 11
Nhằm mang đến cho học sinh lớp 11 có thêm nhiều tài liệu học chương trình Hình học 11 chương 3, Eballsviet.com xin giới thiệu tài liệu Chuyên đề vectơ trong không gian, quan hệ vuông góc.
Tài liệu gồm 99 trang với đầy đủ lý thuyết, dạng toán và bài tập chủ đề vectơ trong không gian, quan hệ vuông góc, sẽ giúp các em dễ dàng tiếp cận và học tốt hơn hình học không gian. Sau đây là nội dung chi tiết mời các em cùng tham khảo và tải tài liệu tại đây.
Chuyên đề vectơ trong không gian, quan hệ vuông góc

GV. TR
GV. TRGV. TR
GV. TRẦ
ẦẦ
ẦN QU
N QUN QU
N QUỐ
ỐỐ
ỐC NGH
C NGHC NGH
C NGHĨA
ĨAĨA
ĨA
1
11
1
VÉCTƠ TRONG KHÔNG GIAN
QUAN HỆ VUÔNG GÓC
Vấn đề 1. VÉCTƠ TRONG KHÔNG GIAN
I. Véctơtrongkhônggian
①
①①
① Véctơ, giá và độ dài của véctơ.
Véctơ trong không gian là một đoạn thẳng có hướng. Kí hiệu
AB
chỉ véctơ có điểm đầu
A
, điểm cuối
B
. Véctơ còn được kí hiệu
a
,
b
,
c
, …
Giá của véctơ là đường thẳng đi qua điểm đầu và điểm cuối của véctơ đó. Hai véctơ được
gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau. Ngược lại, hai véctơ có
giá cắt nhau được gọi là hai véctơ không cùng phương. Hai véctơ cùng phương thì có thể
cùng hướng hoặc ngược hướng.
Độ dài của véctơ là độ dài của đoạn thẳng có hai đầu mút là điểm đầu và điểm cuối của
véctơ. Véctơ có độ dài bằng 1 gọi là véctơ đơn vị. Kí hiệu độ dài véctơ
AB
là
AB
Như vậy:
AB AB BA
= =
.
②
②②
② Hai véctơ bằng nhau, đối nhau. Cho hai véctơ
a
,
b
(≠
0
)
Hai véctơ
a
và
b
được gọi là bằng nhau nếu chúng có cùng hướng và cùng độ dài.
Kí hiệu
a b
=
và
| | | |
a b
a b
a b
= ⇔
=
cuøng höôùng
Hai véctơ
a
và được gọi là đối nhau nếu chúng ngược hướng và cùng độ dài.
Kí hiệu
a b
= −
và
| | | |
a b
a b
a b
= ⇔
=
cuøng höôùng
③
③③
③ Véctơ – không.
Véctơ – không là véctơ có điểm đầu và điểm cuối trùng nhau.
Kí hiệu:
0
,
... 0
AA BB CC
= = = =
.
Véctơ – không có phương, hướng tùy ý, có độ dài bằng không.
Véctơ – không cùng phương, cùng hướng với mọi véctơ.
II.Phépcộngvàphéptrừvéctơ
①
①①
① Định nghĩa 1.
Cho
a
và
b
. Trong không gian lấy một điểm A tùy ý, dựng
AB a
=
,
BC b
=
. Véctơ
AC
được gọi là tổng của hai véctơ
a
và
b
và được kí hiệu
AC AB BC a b
= + = +
.
(
)
a b a b
− = + −
②
②②
② Tính chất 1.
Tính chất giao hoán:
a b b a
+ = +
Tính chất kết hợp:
(
)
(
)
a b c a b c
+ + = + +
Cộng với
0
: 0 0
a a a
+ = + =
Cộng với véctơ đối:
(
)
0
a a a a
+ − = − + =
a
b
A
B
C
a
b
a b
+
8
Chủđề
TÀI LI
TÀI LITÀI LI
TÀI LIỆ
ỆỆ
ỆU H
U HU H
U HỌ
ỌỌ
ỌC T
C TC T
C TẬ
ẬẬ
ẬP TOÁN 11
P TOÁN 11P TOÁN 11
P TOÁN 11
–
––
–
HK2
HK2HK2
HK2
2
22
2
③
③③
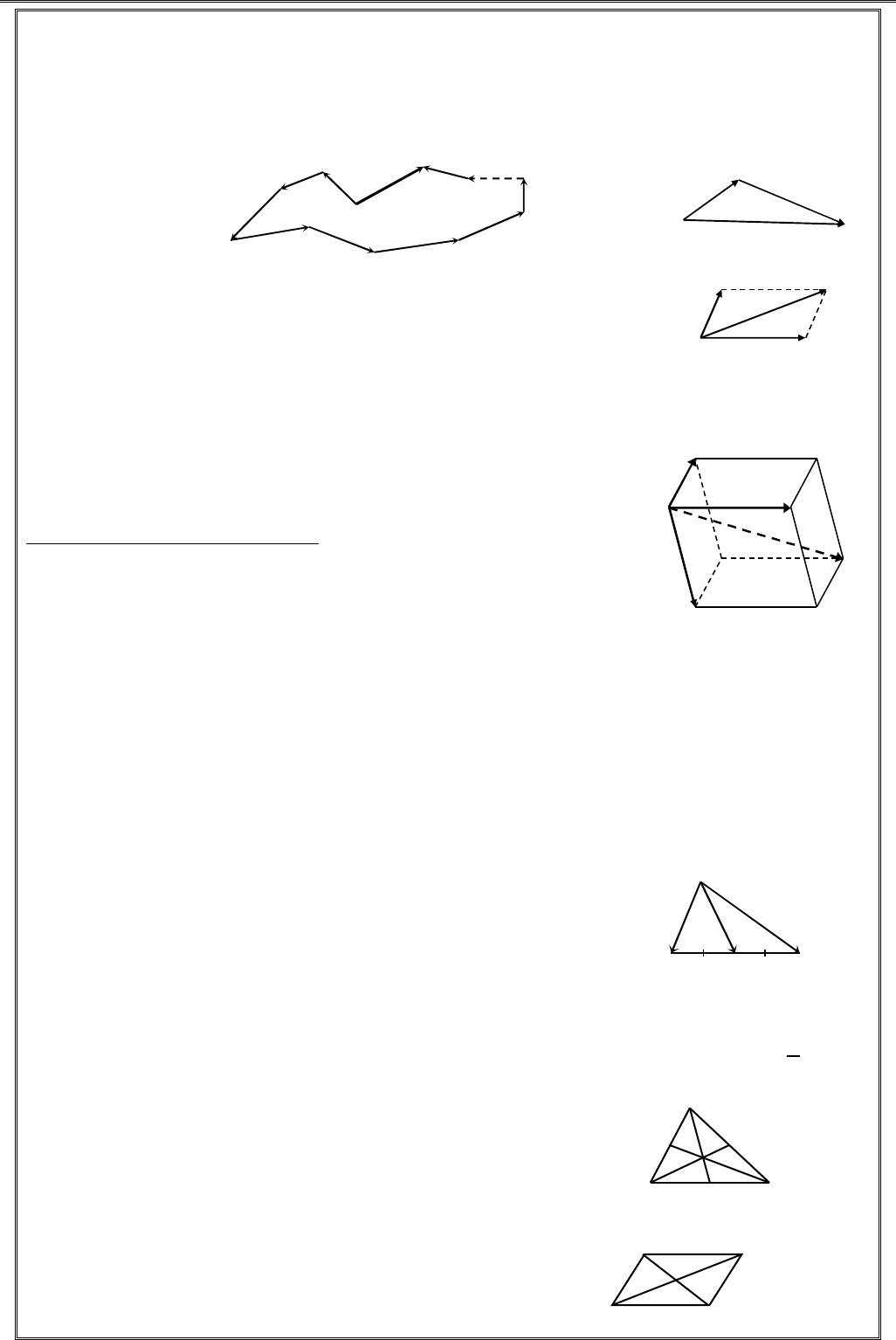
③ Các qui tắc.
Qui tắc ba điểm: Với ba điểm
A
,
B
,
C
bất kì ta có:
AC AB BC
= +
Mở rộng: Qui tắc đa giác khép kín
Cho
n
điểm bất kì
1 2 3 –1
, , , , ,
n n
A A A A A
…
. Ta có:
1 2 2 3 1 1
n n n
A A A A A A A A
−
+ + + =
…
Qui tắc trừ (ba điểm cho phép trừ):
Với ba điểm
A
,
B
,
C
bất kì ta có:
AC BC BA
= −
Qui tắc hình bình hành:
Với hình bình hành
ABCD
ta có:
AC AB AD
= +
và
DB AB AD
= −
Qui tắc hình hộp.
Cho hình hộp .
ABCD A B C D
′ ′ ′ ′
với
AB
,
AD
,
AA
′
là ba cạnh
có chung đỉnh
A
và
AC
′
là đường chéo, ta có:
AC AB AD AA
′ ′
= + +
III.Phépnhânmộtsốvớimộtvéctơ
①
①①
① Định nghĩa 2.
Cho
0
k
≠
và véctơ
0
a
≠
. Tích
.
k a
là một véctơ:
- Cùng hướng với
a
nếu
0
k
>
- Ngược hướng với
a
nếu
0
k
<
②
②②
② Tính chất 2. Với
a
,
b
bất kì;
,
m n R
∈
, ta có:
(
)
m a b ma mb
+ = +
(
)
m n a ma na
+ = +
(
)
(
)
m na mn a
=
1.
a a
=
,
(
)
1 .
a a
− = −
0. 0
a
=
;
.0 0
k
=
③
③③
③ Điều kiện để hai véctơ cùng phương.
Cho hai véctơ
a
và
b
(
0
≠
),
0
k
≠
:
a
cùng phương
b
⇔
a kb
=
Hệ quả: điều kiện để ba điểm
A
,
B
,
C
thẳng hàng là
AB k AC
=
④
④④
④ Một số tính chất.
Tính chất trung điểm
Cho đoạn thẳng
AB
có
I
là trung điểm, ta có:
0
IA IB
+ =
;
IA IB
= −
;
1
2
AI IB AB
= =
2
MA MB MI
+ =
(
M
bất kì)
Tính chất trọng tâm.
Cho
ABC
∆
,
G
là trọng tâm, ta có:
0
GA GB GC
+ + =
3
MA MB MC MG
+ + =
(
M
bất kì)
Tính chất hình bình hành.
Cho hình bình hành
ABCD
tâm
O
, ta có:
0
OA OB OC OD
+ + + =
4
MA MB MC MD MO
+ + + =
1
A
2
A
3
A
4
A
5
A
7
A
8
A
9
A
10
A
n-1
A
n
A
A
B
C
A
B
C
D
A
B
C
D
A'
B'
C'
D'
M
A
I
B
A
B
C
G
A
B
C
D
O
GV. TR
GV. TRGV. TR
GV. TRẦ
ẦẦ
ẦN QU
N QUN QU
N QUỐ
ỐỐ
ỐC NGH
C NGHC NGH
C NGHĨA
ĨAĨA
ĨA
3
33
3
IV.Điềukiệnđểbavéctơđồngphẳng
①
①①
① Khái niện về sự đồng phẳng của ba véctơ trong không gian.
Cho ba véctơ
a
,
b
,
c
(≠
0
) trong không gian. Từ một điểm O bất kì ta dựng
OA a
=
,
OB b
=
,
OC c
=
. Khi đó xảy ra hai trường hợp:
Các đường thẳng
OA
,
OB
,
OC
không cùng nằm trong một mặt phẳng thì ta nói ba véctơ
a
,
b
,
c
không đồng phẳng.
Các đường thẳng
OA
,
OB
,
OC
cùng nằm trong một mặt phẳng thì ta nói ba véctơ
a
,
b
,
c
đồng phẳng.
②
②②
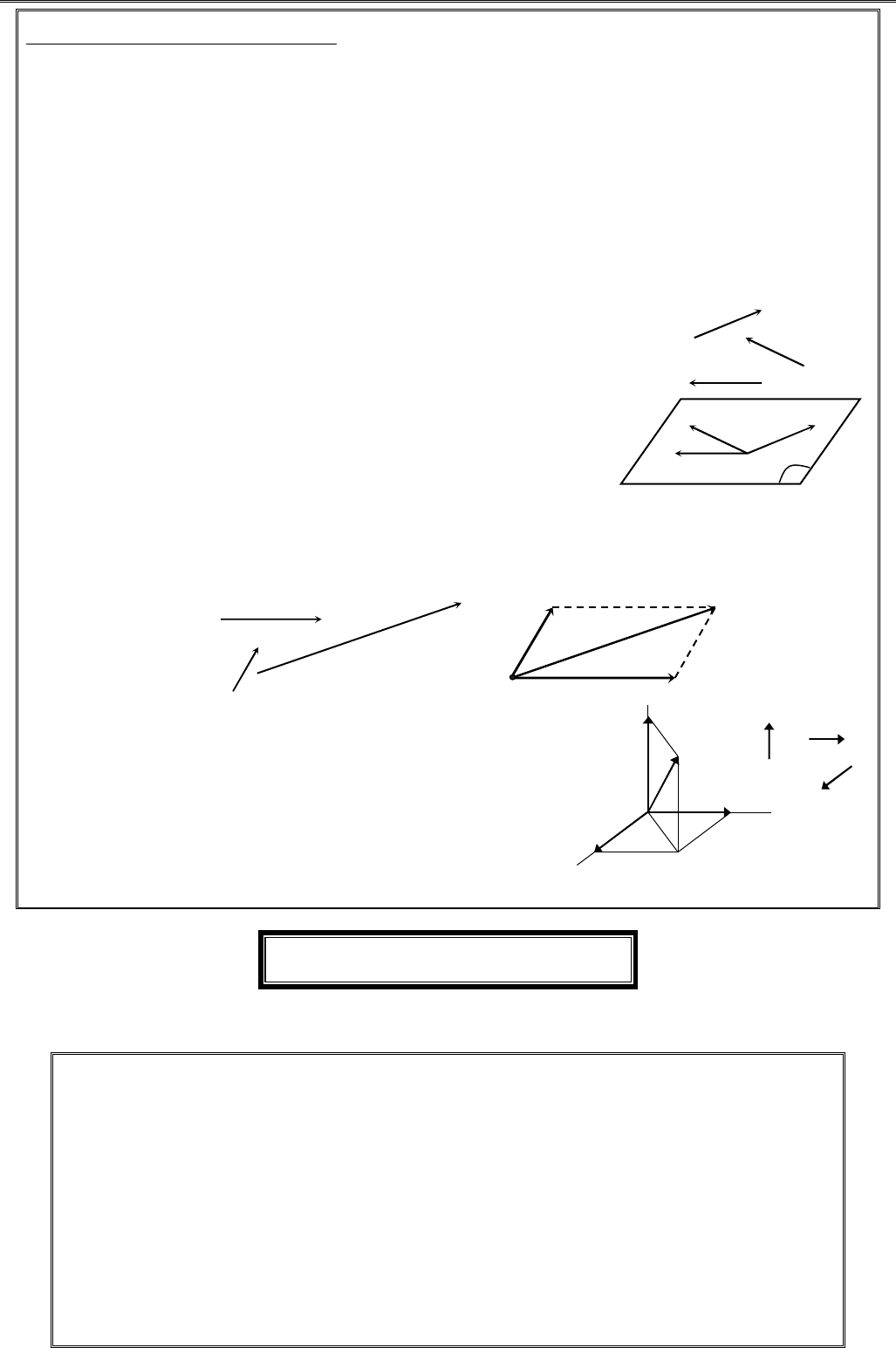
② Định nghĩa 3.
Ba véctơ gọi là đồng phẳng nếu các giá của chúng cùng song song
với một mặt phẳng.
Trên hình bên, giá của các véctơ
a
,
b
,
c
cùng song song với mặt
phẳng (α) nên ba véctơ
a
,
b
,
c
đồng phẳng.
③
③③
③ Điều kiện để ba véctơ đồng phẳng
Định lí 1.
Cho ba véctơ
a
,
b
,
c
trong đó
a
và
b
không cùng phương. Điều kiện cần và đủ để ba
véctơ
a
,
b
,
c
đồng phẳng là có duy nhất các số
m
,
n
sao cho
c ma nb
= +
.
④
④④
④ Phân tích một véctơ theo ba véctơ không đồng phẳng
Định lí 2.
Nếu ba véctơ
a
,
b
,
c
không đồng phẳng thì với mỗi
véctơ
d
, ta tìm được duy nhất các số
m
,
n
,
p
sao cho
d ma nb pc
= + +
.
Dạng1.Tínhtoánvéctơ
A. PHƯƠNG PHÁP GIẢI
①
①①
① Quy tắc ba điểm:
AB AC CB
= +
(quy tắc cộng)
AB CB CA
= −
(quy tắc trừ)
②
②②
② Quy tắc hình bình hành: Với hình bình hành
ABCD
ta luôn có:
AC AB AD
= +
③
③③
③ Quy tắc hình hộp: Cho hình hộp .
ABCD A B C D
′ ′ ′ ′
, ta được:
AC AB AD AA
′ ′
= + +
④
④④
④ Quy tắc trung điểm: Cho
I
là trung điểm
AB
,
M
là điển bất kỳ:
0
IA IB
+ =
và
2
MA MB MI
+ =
⑤
⑤⑤
⑤ Tính chất trọng tâm của tam giác:
G
là trọng tâm
ABC
∆
,
M
∀
ta có:
0
GA GB GC
+ + =
và 3
MA MB MC MG
+ + =
a
b
c
OO
B
A
c
m.a
n.b
a
b
c
O
A
ma
nb
pc
d
D'
D
O
C
A
B
a
b
c
α
Liên kết tải về
Chuyên đề vectơ trong không gian, quan hệ vuông góc
1,2 MB
Tải về
Có thể bạn quan tâm
-

Bộ đề ôn thi THPT Quốc gia môn Toán năm 2023 (40 đề + đáp án)
-

Viết đoạn văn ngắn tả ảnh Bác Hồ (53 mẫu)
-

Văn mẫu lớp 11: Phân tích khổ 2 bài thơ Đây thôn Vĩ Dạ (3 Dàn ý + 15 mẫu)
-
Thuyết minh về trò chơi dân gian nhảy dây (Dàn ý + 7 mẫu)
-

Văn mẫu lớp 10: Phân tích 18 câu thơ đầu trong đoạn trích Trao duyên (2 Dàn ý + 9 mẫu)
-

Văn mẫu lớp 9: Đoạn văn suy nghĩ về lãng phí thời gian (8 mẫu)
-

Bộ đề đọc hiểu Thơ 8 chữ (Có đáp án)
-

Văn mẫu lớp 11: Phân tích quá trình tha hóa của Chí Phèo (Sơ đồ tư duy + 15 mẫu)
-
63 bài tập đọc cho học sinh lớp 1 - Bài tập luyện kỹ năng đọc cho học sinh lớp 1
-

Văn mẫu lớp 10: Phân tích nhân vật An Dương Vương (2 Dàn ý + 13 mẫu)
Xác thực tài khoản!
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:
Số điện thoại chưa đúng định dạng!
Sắp xếp theo
Đóng
Chỉ thành viên Download Pro tải được nội dung này!
Download Pro - Tải nhanh, website không quảng cáo!
Tìm hiểu thêm












