Chuyên đề đạo hàm và ý nghĩa của đạo hàm Tài liệu ôn tập môn Toán lớp 11
Chuyên đề đạo hàm và ý nghĩa của đạo hàm là tài liệu vô cùng hữu ích mà Eballsviet.com muốn giới thiệu đến các bạn học sinh lớp 11, 12 cùng tham khảo.
Chủ đề đạo hàm là phần kiến thức cơ bản và là nên tảng đề các bạn học sinh tìm hiểu sâu hơn về ý nghĩa của đạo hàm nói chung và phương trình tiếp tuyến của hàm số nói riêng. Từ năm tuyển sinh 2018, bộ GD&ĐT đã đưa thêm phần kiến thức của khối lớp 11 vào cấu trúc đề thi, do đó các bạn học sinh cần chuẩn bị những kiến thức căn bản để có thể sử dụng một cách nhanh gọn các đề thi trắc nghiệm. Nội dung chi tiết tài liệu mời các bạn cùng tham khảo và tải tại đây.
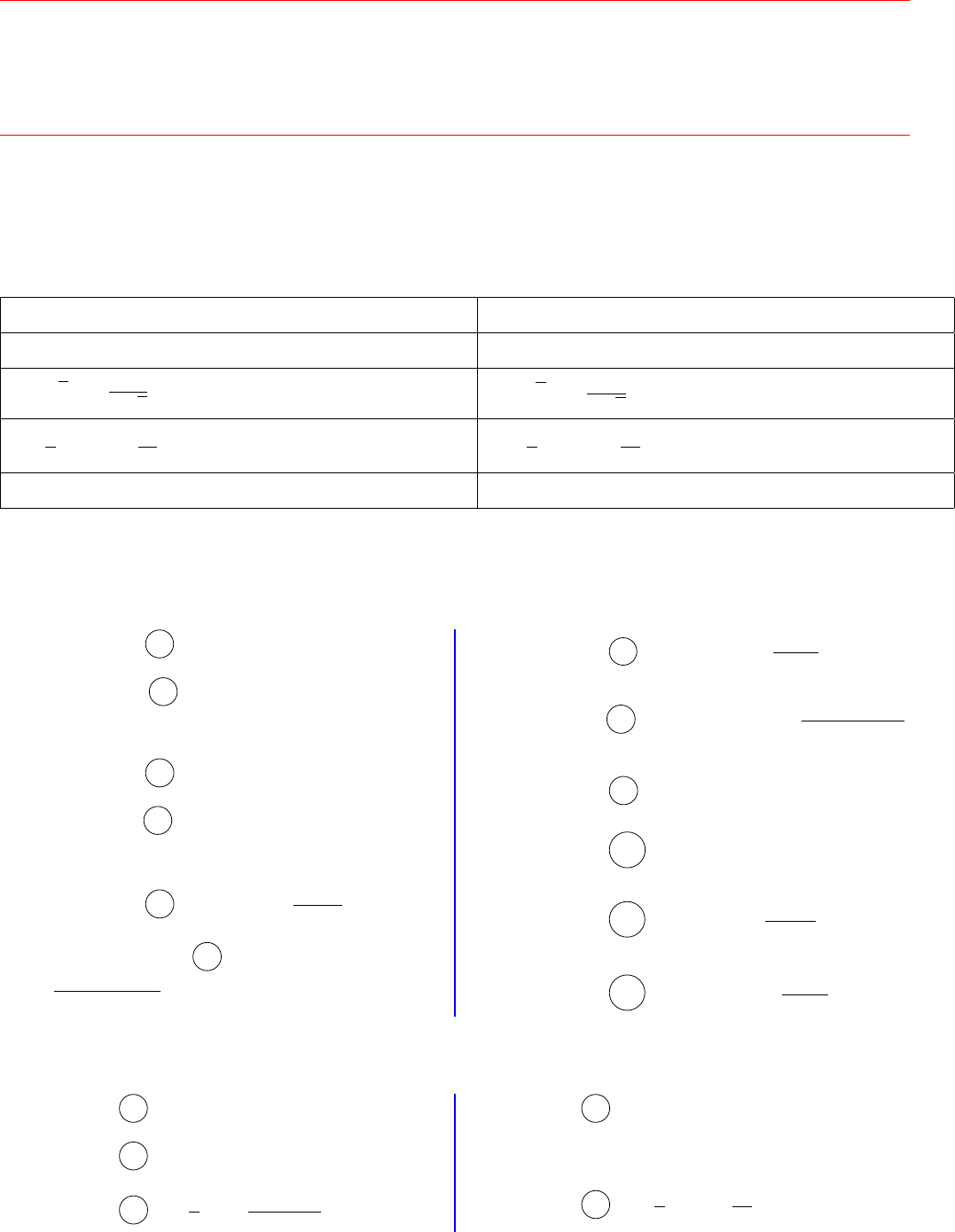
Chuyên đề đạo hàm và ý nghĩa của đạo hàm
MỤC LỤC
Chương 1 ÔN TẬP: Đạo hàm và ứng dụng 2
1.1 Các công thức cần nhớ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
1.2 Ý nghĩa hình học của đạo hàm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
1.2.1 Ý nghĩa hình học của đạo hàm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
1.2.2 Viết phương tr ình tiếp tuyến tại điểm giao với trục Ox,Oy hoặc giao với đồ thị hàm
số khác . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
1.2.3 Viết phương trình tiếp tuyến biết hệ số góc . . . . . . . . . . . . . . . . . . . . . . 8
1.2.4 Viết phương trình tiếp tuyến qua điểm cho trước . . . . . . . . . . . . . . . . . . . . 11
1.2.5 Các bài toán tiếp tuyến chứa tham số m . . . . . . . . . . . . . . . . . . . . . . . . 12
1.3 Ý nghĩa vật lý của đạo hàm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
1.3.1 Ý nghĩa vật lý của đạo hàm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
1.4 Các bài toán liên quan đến đạo hàm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
1.4.1 Các bài toán liên quan đến đạo hàm . . . . . . . . . . . . . . . . . . . . . . . . . . 15
1.5 Đáp án . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
1.6 Lời giải chi tiết . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20
1
CHƯƠNG 1
ÔN TẬP: ĐẠO HÀM VÀ ỨNG DỤNG
§1.1 Các công thức cần nhớ
1. c
0
= 0 2. x
0
= 1
3.
x
n
0
= n.x
n−1
(n ∈ N,n > 1) 4.
u
n
0
= n.u
n−1
.u
0
(n ∈ N,n > 1)
5. (
√
x)
0
=
1
2
√
x
6. (
√
u)
0
=
u
0
2
√
u
7.
1
x
0
= −
1
x
2
8.
1
u
0
= −
u
0
u
2
9. (kx)
0
= k 10. (ku)
0
= k.u
0
Bảng 1.1: Bảng đạo hàm các hàm cơ bản
Đạo hàm của hàm lượng giác
1. Công thức 1 . (sin x)
0
= cos x.
2. Công thức 2 . (sin(ax + b))
0
= a cos(ax +
b).
3. Công thức 3 . (cos x )
0
= −sin x.
4. Công thức 4 . (cos(ax+b))
0
= −a sin(ax +
b).
5. Công thức 5 . (tan x )
0
=
1
cos
2
x
.
6. Công thức 6 . (tan(ax + b))
0
=
a
cos
2
(ax + b)
.
7. Công thức 7 . (cot x)
0
= −
1
sin
2
x
.
8. Công thức 8 . (cot(ax+b))
0
= −
a
sin
2
(ax + b)
.
9. Công thức 9 . (sin u)
0
= u
0
.cos u.
10. Công thức 10 . (cos u)
0
= −u
0
.sin u.
11. Công thức 11 . (tan u)
0
=
u
0
cos
2
u
.
12. Công thức 12 . (cot u)
0
= −
u
0
sin
2
u
.
Các quy tắc tính đạo hàm
1. Qui tắc 1 . (u ±v)
0
= u
0
±v
0
.
2. Qui tắc 2 . (uv)
0
= u
0
v + uv
0
.
3. Qui tắc
3 .
u
v
0
=
u
0
v −uv
0
v
2
.
4. Hệ quả 1 . (ku)
0
= ku
0
.
5. Hệ quả 2 .
1
u
0
= −
u
0
u
2
.
Các định lý nghiệm tam thức f (x) = ax
2
+ bx + c
2
CHƯƠNG 1. ÔN TẬP: ĐẠO HÀM VÀ ỨNG DỤNG Thầy Lê Minh Cường - 01666658231
1. f (x) = 0 có 2 nghiệm phân biệt ⇔
a 6= 0
∆ > 0
.
2. f (x) = 0 có nghiệm kép ⇔
a 6= 0
∆ = 0
.
3. f (x) = 0 có 2 nghiệm trái dấu ⇔ ac < 0.
4. f (x) = 0 có 2 nghiệm dương pb ⇔
a 6= 0
∆ > 0
S > 0
P > 0
.
5. f (x) = 0 có 2 nghiệm âm pb ⇔
a 6= 0
∆ > 0
S < 0
P > 0
.
6. f (x) ≤ 0, ∀x ∈ R ⇔
a < 0
∆ ≤ 0
.
7. f (x) ≥ 0, ∀x ∈ R ⇔
a > 0
∆ ≤ 0
.
Định lý Vi-ét: Nếu x
1
,x
2
là 2 nghiệm phân biệt của ax
2
+ bx + c = 0 thì
x
1
+ x
2
=
−b
a
x
1
.x
2
=
c
a
.
? Luyện thi 10 - 11 - 12 - THPT QG tại Sài Gòn ? Page 3 of 23
Chia sẻ bởi: 
Trịnh Thị Thanh
Trịnh Thị Thanh Liên kết tải về
Chuyên đề đạo hàm và ý nghĩa của đạo hàm 310,6 KB Tải về
Có thể bạn quan tâm
-
Toán 6 Bài tập cuối chương VI Cánh diều
-
Phân tích bài thơ Mùa thu và mẹ của Lương Đình Khoa
-
Tìm ý cho đoạn văn thuật lại một ngày hội em đã chứng kiến (5 mẫu)
-
Đề cương ôn tập học kì 2 môn Vật lý lớp 9 năm 2023 - 2024
-
Cách viết thư UPU lần thứ 54 năm 2025
-
Văn mẫu lớp 11: Phân tích tác phẩm Vĩnh biệt Cửu Trùng đài (2 Dàn ý + 10 mẫu)
-
Tập làm văn lớp 5: Tả quang cảnh trường em (Dàn ý + 26 Mẫu)
-
Phân tích diễn biến tâm lí nhân vật Phương Định trong một lần phá bom
-
Soạn bài Một số câu tục ngữ Việt Nam - Kết nối tri thức 7
-
So sánh sinh sản vô tính và sinh sản hữu tính
Xác thực tài khoản!
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:
Số điện thoại chưa đúng định dạng!
Sắp xếp theo
