Các trường hợp bằng nhau của tam giác vuông Chuyên đề Toán học lớp 7

Các trường hợp bằng nhau của tam giác vuông là một trong những dạng toán tương đối khó mà nhiều bạn học sinh chưa biết cách giải. Chính vì thế hôm nay Eballsviet.com sẽ giới thiệu đến các bạn các trường hợp bằng nhau của tam giác vuông lớp 7 chi tiết nhất.

Các trường hợp bằng nhau của tam giác vuông bao gồm toàn bộ kiến thức lý thuyết về các trường hợp bằng nhau của tam giác, một số bài tập có đáp án giải chi tiết kèm theo tự luyện. Tài liệu được biên soạn rất chi tiết dễ hiểu, gần gũi với các bạn học sinh. Qua đó các em dễ dàng nắm được kiến thức trọng tâm vận dụng vào giải các bài tập. Bên cạnh đó các em tham khảo thêm: bài tập về lũy thừa số hữu tỉ, bài tập Nhân chia số hữu tỉ.

A. Khái niệm hai tam giác bằng nhau

Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng bằng nhau, các góc tương ứng bằng nhau.

Để kí hiệu sự bằng nhau của tam giác ABC và tam giác A’B’C".

B. Các trường hợp bằng nhau của tam giác vuông

*Hai cạnh góc vuông

Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau (cạnh – góc – cạnh )

*Cạnh góc vuông và góc nhọn kề cạnh đó

Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau ( góc – cạnh – góc )

*Cạnh huyền – góc nhọn

Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau ( góc – cạnh – góc)

*Cạnh huyền – cạnh góc vuông

Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

C. Ví dụ minh họa các trường hợp bằng nhau của tam giác vuông 

Cho ΔABC cân ở A (∠A < 90^o). Vẽ BH ⊥ AC (H ∈ AC), CK ⊥ AB (K ∈ AB).

a) Chứng minh rằng AH = HK

b) Gọi I là giao điểm của BH và CK. Chứng minh rằng AI là tia phân giác của góc A

Trả lời 

Vẽ hình minh họa:

a) ΔABC cân tại A (giả thiết)

Suy ra

AB = AC (tính chất)

\(\widehat{ABC} = \widehat{ACB}\)(định lí)

Xét hai tam giác vuông HAB và KAC, ta có:

AB = AC (chứng minh trên)

\(\widehat{A}\) chung

⇒ ΔHAB = ΔKAC (cạnh huyền - góc nhọn)

⇒ AH = AK (cặp cạnh tương ứng)

b) Xét hai tam giác vuông KAI và HAI, ta có:

AH = AK (chứng minh trên)

AI cạnh chung

⇒ ΔHAI = ΔKAI (cạnh huyền - cạnh góc vuông)

\(\Rightarrow \widehat{KAI} = \widehat{HAI}\)(cặp góc tương ứng)

Hay AI là tia phân giác của \(\widehat{A}\)

D. Bài tập các trường hợp bằng nhau của tam giác vuông (Có đáp án)

Bài tập 1: Các tam giác vuông ABC và DEF có góc A = góc D = 90^o, AC = DF. Hãy bổ sung thêm một điều kiện bằng nhau để ΔABC = ΔDEF.

Trả lời

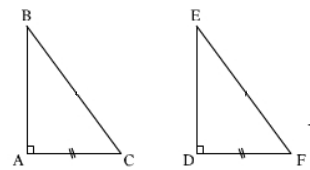
+ Bổ sung AB =DE thì ΔABC = ΔDEF (cạnh - góc - cạnh)

+ Bổ sung \(\widehat{C} = \widehat{F}\) thì ΔABC = ΔDEF (góc - cạnh - góc)

+ Bổ sung BC = EF thì ΔABC = ΔDEF (cạnh huyền - cạnh góc vuông)

Bài tập 2: Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC. Chứng minh rằng

a) HB = HC

b) góc BAH = góc CAH

Trả lời

a) Xét hai tam giác vuông ΔABH và ΔACH có:

AB = AC (giả thiết)

AH cạnh chung

⇒ ΔABH = ΔACH (cạnh huyền - cạnh góc vuông)

Suy ra HB = HC (cặp cạnh tương ứng)

b) Ta có ΔABH = ΔACH (chứng minh trên)

\(\Rightarrow \widehat{BAH} = \widehat{CAH}\)(cặp góc tương ứng)

Bài tập 3

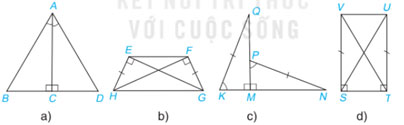
Mỗi hình sau có các cặp tam giác vuông nào bằng nhau? Vì sao?

Gợi ý đáp án:

a) Xét 2 tam giác vuông ABC và ADC có:

\(\widehat {ACB} = \widehat {ACD}( = 90^\circ )\)

AC chung

\(\widehat {BAC} = \widehat {DAC}(gt)\)

\(=>\Delta ABC = \Delta ADC(g.c.g)\)

b) Xét 2 tam giác vuông HEG và GFH có:

HE=GF(gt)

HG chung

\(=>\Delta HEG = \Delta GFH(c.h-c.g.v)\)

c) Xét 2 tam giác vuông QMK và NMP có:

QK=NP

\(\widehat K = \widehat P\)

\(=>\Delta QMK = \Delta NMP\)(cạnh huyền – góc nhọn)

d) Xét 2 tam giác vuông VST và UTS có:

VS=UT

ST chung

\(=>\Delta VST = \Delta UTS(c.g.c)\)

Bài tập 4

Cho hình 4.56, biết \(AB=CD, \widehat {BAC} = \widehat {BDC} = {90^o}\). Chứng minh rằng \(\Delta ABE = \Delta DCE\).

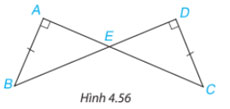
Gợi ý đáp án:

Vì tổng 3 góc trong 1 tam giác luôn bằng 180 độ.

Xét hai tam giác AED và DEC có:

\(\widehat {AEB} = \widehat {DEC}\)(đối đỉnh) và \(\widehat {BAC} = \widehat {BDC} = {90^o}\).

Suy ra: \(\widehat {AEB} = \widehat {DEC}\)

Xét 2 tam giác vuông AEB và DEC có:

AB=DC

\(\widehat {AEB} = \widehat {DEC}\)

\(=>\Delta AEB = \Delta DEC(g.c.g)\)

Bài tập 5

Cho hình chữ nhật ABCD, M là trung điểm của cạnh BC.

Chứng minh rằng \(\Delta ABM = \Delta DCM\).

Gợi ý đáp án:

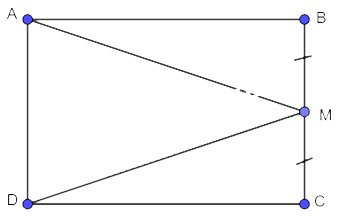
Xét 2 tam giác vuông ABM và DCM có:

AB=DC (tính chất hình chữ nhật)

BM=CM (gt)

\(=>\Delta ABM = \Delta DCM(c.g.c)\)

Bài tập 6

Cho ba điểm A, B, C nằm trên đường tròn tâm O và các điểm M, N, P như Hình 4.54. Hãy chỉ ra ba cặp tam giác vuông bằng nhau trong hình.

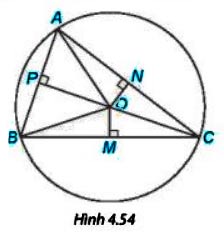
Gợi ý đáp án:

Do A, B, C nằm trên đường tròn tâm O

=> OA = OB = OC = R

Xét tam giác AOP vuông tại P và tam giác BOP vuông tại P ta có:

OA = OB (giả thiết)

PO là cạnh chung

=> ∆AOP = ∆BOP (cạnh huyền cạnh – cạnh góc vuông)

Xét tam giác AON vuông tại N và tam giác CON vuông tại N ta có:

OA = OC (giả thiết)

ON là cạnh chung

=> ∆AON = ∆CON (cạnh huyền cạnh – cạnh góc vuông)

Xét tam giác BOM vuông tại M và tam giác COM vuông tại M ta có:

OB = OC (giả thiết)

OM là cạnh chung

=> ∆BOM = ∆COM (cạnh huyền cạnh – cạnh góc vuông)

E. Bài tập trường hợp bằng nhau của tam giác vuông

I. Lý thuyết:

Câu 1: Phát biểu các trường hợp bằng nhau của tam giác? Vẽ hình minh họa cho mỗi trường hợp?

Câu 2: Phát biểu các trường hợp bằng nhau của tam giác vuông? Vẽ hình minh họa cho mỗi trường hợp?

Câu 3: Phát biểu định lí một đường thẳng vuông góc với mọt trong hai đường thẳng song song? Ghi giả thiết kết luận? Vẽ hình minh họa?

Câu 4: Phát biểu định lí hai đường thẳng cùng vuông góc với một đường thẳng? Ghi giả thiết kết luận? Vẽ hình minh họa?

Câu 5: Phát biểu định lí ba đường thẳng song song? Ghi giả thiết kết luận? Vẽ hình minh?

Câu 6: Các em tự tìm hiểu những t/c, định lí nào có liêu quan đến các trường hợp bằng nhau của tam giác? Kể tên?

II. Bài tập:

A. Bài tập tự luận

Bài 1: Cho tam giác ABC có \(\widehat{\mathrm{A}}=40^{\circ}, \mathrm{AB}=\mathrm{AC}\). Gọi M là trung điểm của BC. Tính các góc của tam giác AMB và tam giác AMC.

Bài 2. Cho tam giác ABC có D, E thuộc cạnh BC sao cho BD = DE = EC. Biết AD = AE. Biết
\(\mathrm{AD}=\mathrm{AE}\)

a) Chứng minh \(\widehat{\mathrm{EAB}}=\widehat{\mathrm{DAC}}.\)

b) Gọi M là trung điểm của BC. Chứng minh AM là phân giác của \(\widehat{DAE }\)

c) Giả sử \(\widehat{\mathrm{DAE}}=60^{\circ}\). Tính các góc còn lai của tam giác DAE.

Bài 3. Cho tam giác ABC vuông ở A. Trên tia đối của tia AC lấy điểm D sao cho AD = AC.

a) Chứng minh DABC = DABD

b) Trên tia đối của tia AB, lấy điểm M. Chứng minh DMBD = D MBC.

Bài 4. Cho góc nhọn xOy và tia phân giác Oz của góc đó. Trên Ox, lấy điểm A, trên Oy lấy điểm B sao cho OA = OB. Trên tia Oz, lấy điểm I bất kì. Chứng minh:

a) D AOI = D BOI.

b) AB vuông góc OI..

Bài 5. Cho \(\triangle \mathrm{ABC}\) có \(\mathrm{AB}<\mathrm{AC}\). Kẻ tia phân giác \(\mathrm{AD}\) của \(\widehat{\mathrm{BAC}}\) ( D thuộc BC). Trên canh AC lấy điểm E sao cho A E=A B, trên tia A B lấy điểm F sao cho A F=A C. Chứng minh rằng:

\(a) \Delta \mathrm{BDF}=\Delta \mathrm{EDC}.\)

\(b) \mathrm{BF}=\mathrm{EC}.\)

c) FDE thẳng hàng.

\(d) \mathrm{AD} \perp \mathrm{FC}\)

Bài 6. Cho góc nhọn \(\mathrm{xOy}\). Trên tia Ox, lấy 2 điểm A và C. Trên tia Oy lấy 2 điểm B và D sao cho OA=OB ;OC=OD. (A nằm giữa O và C; B Nằm giữa O và D).

a) Chứng minh \(\Delta \mathrm{OAD}=\Delta \mathrm{OBC}\)

b) So sánh 2 góc \(\widehat{\mathrm{CAD}}\) và \(\widehat{\mathrm{CBD}}.\)

Bài 7. Cho DABC vuông ở A. Trên tia đối của tia AC lấy điểm D sao cho AD = AC.

a) Chứng minh DABC = DABD

b) Trên tia đối của tia AB, lấy điểm M. Chứng minh DMBD = D MBC.

Bài 8. Cho góc nhọn xOy và tia phân giác Oz của góc đó. Trên Ox, lấy điểm A, trên Oy lấy điểm B sao cho OA = OB. Trên tia Oz, lấy điểm I bất kì. Chứng minh:

a) D AOI = D BOI.

b) AB vuông góc OI.

Bài 9. Cho DABC, M là trung điểm của BC. Trên tia đối của tia MA, lấy điểm E sao cho ME = MA.

a) Chứng minh AC // BE.

b) Gọi I là một điểm trên AC, K là một điểm trên EB sao cho AI = EK. Chứng minh 3 điểm I, M, K thẳng hàng.

Bài 10. Cho \(\triangle \mathrm{ABC}\) vuông tai \(\mathrm{A}, có =53^{0}\)

a) Tính \(\widehat{\mathrm{C}}\)

b) Trên canh \(\mathrm{BC}\), lấy điểm D sao cho BD=BA. Tia phân giác của góc B cắt cạnh AC tai E. Chứng minh \(\Delta \mathrm{BEA}=\Delta \mathrm{BED}\)

c) Qua c, vẽ đường thẳng vuông góc với BE tại H, CH cắt AB tại F. Chứng minh \(\Delta \mathrm{BHF}=\Delta \mathrm{BHC}\)

d) Chứng minh \(\Delta \mathrm{BAC}=\Delta \mathrm{BDF}\) và ba điểm D, E, F thẳng hàng

Bài 11. Cho \(\triangle \mathrm{ABC}\), có \(\mathrm{AB}=\mathrm{AC}\) và M là trung điểm của BC

a) Chứng minh \(\triangle \mathrm{AMB}=\Delta \mathrm{AMC}\)

b) Qua A vẽ \(a \perp A M.\) Chứng minh \(A M \perp B C\) và a / / B C

c) Qua C, vẽ b/ / AM. Goi N là giao điểm của hai đường thẳng a và b. Chứng minh \(\triangle \mathrm{AMC}=\Delta \mathrm{CNA}\)

d) Gọi I là trung điểm của đoạn AC. Chứng minh I là trung điểm của đoạn MN

Bài 12. Cho \(\triangle \mathrm{ABC}\), gọi M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho MD=MA. Chứng minh rằng:

a)\(\triangle \mathrm{MAB}=\Delta \mathrm{MDC}\)

b) AB = AC và AB//CD

c) \(\widehat{\mathrm{BAC}}=\widehat{\mathrm{CDB}}\)

d) Trên các đoạn thẳng AB, CD lần lượt lấy các điểm E, F sao cho AE=AF. Chứng minh E, M, F thẳng hàng

Bài 13. Cho \(\triangle \mathrm{ABC}\) vuông tai \(\mathrm{A}(\mathrm{AB}<\mathrm{AC})\). Tia phân giác của \(\widehat{\mathrm{B}}\) cắt AC tại D. Trên cạnh BC lấy điểm E sao cho BE= BA. Vẽ \(\mathrm{AH} \perp \mathrm{BC}\)  tại H. Chứng minh rằng:

a) \(\triangle \mathrm{ABD}=\Delta \mathrm{EBD}\) và \(\mathrm{AD}=\mathrm{ED}\)

b) \(\mathrm{AH} / / \mathrm{DE}\)

c) Trên tia \(\mathrm{DE}\) lấy điểm K sao cho DK=AH. Gọi M là trung điểm của đoan DH

Chứng minh A, M, K thẳng hàng

Bài 14. Cho \(\triangle \mathrm{ABC}\), Gọi D là trung điểm của AB. Qua D kẻ đường thẳng song song với BC cắt AC tại E, qua E kẻ đường thẳng song song với AB cắt BC tại F. Chứng minh rằng:

a) AD = EF

b) AE = EC

Bài 15. Cho \(\triangle \mathrm{ABC}\). Gọi M, N thứ tự là trung điểm của AB và AC. Lấy P sao cho N là trung điểm của MP. Chứng minh rằng:

\(a) \mathrm{CP} / / \mathrm{AB} ; \mathrm{CP}=\frac{1}{2} \mathrm{AB}\)

b) \(\triangle \mathrm{BMC}=\triangle \mathrm{PCM}\), Từ đó suy ra \(\mathrm{MN} / / \mathrm{BC} ; \mathrm{MN}=\frac{1}{2} \mathrm{BC}\)

Bài 16. Cho \(\widehat{x O y}\) nhọn. Lấy A trên Ox, B trên Oy sao cho OA=OB. Qua A kẻ đưởng thẳng vuông góc với \(\mathrm{Ox}\) cắt Oy tại M, qua B kẻ đt vuông góc Oy cắt Ox tại N. Gọi H là giao điểm của AM và BN, I là trung điểm của MN. Chứng minh rằng:

a) ON = OM

b) Ba điểm O, H, I thẳng hàng

Bài 17. Cho \(\triangle \mathrm{ABC}\) có \(\widehat{\mathrm{A}}=60^{\circ}\), kẻ \(\mathrm{BD}, \mathrm{CE}\) là các tia phân giác của \(\widehat{\mathrm{B}}, \widehat{\mathrm{C}} (\mathrm{D} \in \mathrm{AC} ; \mathrm{E} \in \mathrm{AB}). \mathrm{BD}\) cắt \(\mathrm{CE}\) tại I

a) Tính \(\widehat{\mathrm{BIC}}\)

b) Kẻ IF là các tia phân giác của \(\widehat{\mathrm{BIC}}(\mathrm{F} \in \mathrm{BC})\). Chứng minh rằng:

\(\begin{aligned} &\text { +) } \triangle \mathrm{BEI}=\Delta \mathrm{BFI} \\ &\text { +) } \mathrm{BE}+\mathrm{CD}=\mathrm{BC} \\ &\text { +) } \mathrm{ID}=\mathrm{IE}=\mathrm{IF} \end{aligned}\)

Bài 18. Cho \(\triangle \mathrm{ABC}\) nhọn. Vẽ về phía ngoài \(\triangle \mathrm{ABC}\) các đoạn thẳng \(\mathrm{BD}=\mathrm{BA}\) và \(\mathrm{CE}=\mathrm{CA}.\)

Kẻ \(\mathrm{DH}\), EK vuông góc với đường thẳng \(\mathrm{BC}(\mathrm{H}, \mathrm{K} \in \mathrm{BC})\). Chứng minh rằng:

\(\mathrm{DH}+\mathrm{EK}=\mathrm{BC}\)

Bài 19. Cho \(\triangle \mathrm{ABC}\). Trên cạnh AB lấy M và N sao cho AM = BN. Qua M và N kẻ các đt song song với BC, cắt AC thứ tự tại D và E. Cmr: \(\mathrm{MD}+\mathrm{NE}=\mathrm{BC}\)

Bài 20 :

Vẽ góc nhọn xAy. Trên tia Ax lấy hai điểm B và C (B nằm giữa A và C). Trên tia Ay lấy hai điểm D và E sao cho AD = AB; AE = AC

a) Chứng minh BE = DC

b) Gọi O là giao điểm BE và DC. Chứng minh tam giác OBC bằng tam giác ODE.

c) Vẽ trung điểm M của CE. Chứng minh AM là đường trung trực của CE.

Bài 21.

Cho tam giác ABC ( AB< AC ) . Gọi I là trung điểm của AC. Trên tia đối của tia IB lấy điểm D, sao cho IB = ID. Chứng minh :

a) Tam giác AIB bằng tam giác CID.

b) AD = BC v à AD // BC.

Bài 22

Cho tam giác ABC có góc A =35⁰ . Đường thẳng AH vuông góc với BC tại H. Trên đường vuông góc với BC tại B lấy điểm D không cùng nửa mặt phẳng bờ BC với điểm A sao cho AH = BD.

a) Chứng minh ΔAHB = ΔDBH.

b) Chứng minh AB//HD.

c) Gọi O là giao điểm của AD và BC. Chứng minh O là trung điểm của BH.

Bài 23: Cho tam giác ABC vuông tại A, phân giác BE (Điểm E thuộc cạnh AC), đường thẳng qua E vuông góc với BC tại D và cắt tia BA tại F:

a. Chứng minh hai tam giác EAB và EDB bằng nhau.

b. So sánh EA và EC va chứng minh EC = EF.

c. Gọi O là giao điểm của đường thẳng BE và CE. Chứng minh OA = OD.

Bài 24: Cho tam giác ABC có AB = AC. Gọi M là trung điểm của BC.

a) Chứng minh hai tam giác ABM và ACM bằng nhau.

b) Chứng minh AM vuông góc BC.

c) Chứng minh AM là phân giác của góc A.

Bài 25: Cho hình vẽ, biết . Chứng minh rằng:

a. ∆ABD = ∆ACD.

b. ∆DBE = ∆DCH.

c. ∆ABH = ∆ACE.

Bài 26: Cho tam giác ABC vuông tại A. Tia phân giác của góc B cắt cạnh AC tại D. Trên cạnh BC lấy điểm H sao cho BH = BA.

a) Chứng minh ∆ABD = ∆HBD.

b) Chứng minh DH vuông góc với BC.

c) Giả sử góc . Tính số đo góc ADB.

Bài 5: cho tam giác ABC vuông tại B, đường phân giác AD (D thuộc BC). Kẻ BO vuông góc với AD (O thuộc AD), BO cắt AC tại E. Chứng minh:

a. ∆ABO = ∆AEO.

b. ∆BAE cân.

c. AD là đường trung trực của BE.

d. Kẻ BK vuông góc với AC (K ∈ AC). Gọi M là giao điểm của BK và AD. Chứng minh rằng ME// BC.

B. Câu hỏi trắc nghiệm

Bài 1: Cho tam giác ABC và tam giác NPM có BC = PM, ∠B = ∠P = 90° . Cần điều kiện gì để tam giác ABC bằng tam giác NPM theo trường hợp cạnh huyền – cạnh góc vuông?

A. BA = PM

B. BA = PN

C. CA = MN

D. ∠A = ∠N

Bài 2: Cho tam giác ABC và tam giác MNP có ∠A = ∠M = 90°, ∠C = ∠P. Cần điều kiện gì để hai tam giác ABC và tam giác MNP bằng nhau theo trường hợp cạnh góc vuông – góc nhọn kề?

A. AC = MP

B. AB = MN

C. BC = NP

D. AC = MN

Bài 3: Cho tam giác ABC và tam giác DEF có: ∠B = ∠E = 90°, AC = DF, ∠A = ∠F. Phát biểu nào sau đây đúng?

A. ΔABC = ΔFED

B. ΔABC = ΔFDE

C. ΔBAC = ΔFED

D. ΔABC = ΔDEF

Bài 4: Cho tam giác ABC và tam giác KHI có: ∠A = ∠K = 90°, AB = KH, BC = HI. Phát biểu nào sau đây đúng?

A. ΔABC = ΔKHI

B. ΔABC = ΔHKI

C. ΔABC = ΔKIH

D. ΔACB = ΔKHI

Bài 5: Cho tam giác ABC và tam giác DEF có AB = DE, ∠B = ∠E, ∠A = ∠D = 90°. Biết AC = 9cm. Tính độ dài DF?

A. 10cm

B. 5cm

C. 9cm

D. 7cm