Bài tập toán lớp 6: Số chính phương Tài liệu số chính phương và những dạng bài tập cơ bản
Nhằm giúp các em học tốt môn Toán lớp 6, Eballsviet.com xin giới thiệu tài liệu "Bài tập toán lớp 6 - Số chính phương" được chúng tôi tổng hợp chi tiết, chính xác nhất.
Hy vọng với tài liệu này, giúp các em củng cố và nâng cao kiến thức và các dạng bài tập về số chính phương. Sau đây là nội dung chi tiết tài liệu, mời các em cùng tham khảo.
Bài tập toán lớp 6: Số chính phương
I. ĐỊNH NGHĨA:
Số chính phương là số bằng bình phương đúng của một số nguyên, với số nguyên bao gồm các số nguyên dương, nguyên âm và số 0. Số chính phương về bản chất là bình phương của một số tự nhiên nào đó.
Hay hiểu một cách khác, số chính phương là một số tự nhiên có căn bậc hai cũng là một số tự nhiên.
Một số chính phương được gọi là số chính phương chẵn nếu như nó là bình phương của một số chẵn. Ngược lại, một số chính phương được gọi là số chính phương lẻ nếu như nó là bình phương của một số lẻ.
II. TÍNH CHẤT:
1. Số chính phương chỉ có thể có chữ số tận cùng bằng 0, 1, 4, 5, 6, 9; không thể có chữ số tận cùng bằng 2, 3, 7, 8.
2. Khi phân tích ra thừa số nguyên tố, số chính phương chỉ chứa các thừa số nguyên tố với số mũ chẵn.
3. Số chính phương chỉ có thể có một trong hai dạng 4n hoặc 4n + 1. Không có số chính phương nào có dạng 4n + 2 hoặc 4n + 3 (n N).
4. Số chính phương chỉ có thể có một trong hai dạng 3n hoặc 3n + 1. Không có số chính phương nào có dạng 3n + 2 (n N).
5. Số chính phương tận cùng bằng 1 hoặc 9 thì chữ số hàng chục là chữ số chẵn.
Số chính phương tận cùng bằng 5 thì chữ số hàng chục là 2
Số chính phương tận cùng bằng 4 thì chữ số hàng chục là chữ số chẵn.
Số chính phương tận cùng bằng 6 thì chữ số hàng chục là chữ số lẻ.
6. Số chính phương chia hết cho 2 thì chia hết cho 4.
Số chính phương chia hết cho 3 thì chia hết cho 9.
Số chính phương chia hết cho 5 thì chia hết cho 25.
Số chính phương chia hết cho 8 thì chia hết cho 16.
III. MỘT SỐ DẠNG BÀI TẬP VỀ SỐ CHÍNH PHƯƠNG
Dạng 1: Chứng minh một số là số chính phương
Bài 1: Chứng minh rằng với mọi số nguyên x, y thì
![]() \(A=(x+y)(x+2y)(x+3y)(x+4y)+y^4\) là số chính phương.
\(A=(x+y)(x+2y)(x+3y)(x+4y)+y^4\) là số chính phương.
Ta có
![]() \(A=(x+y)(x+2y)(x+3y)(x+4y)+y^4\)
\(A=(x+y)(x+2y)(x+3y)(x+4y)+y^4\)
![]() \(=(x^2+5xy+4y^2)(x^2+5xy+6y^2)+y^4\)
\(=(x^2+5xy+4y^2)(x^2+5xy+6y^2)+y^4\)
Đặt ![]() \(x^{2} + 5xy + 5y^{2} = t\)
\(x^{2} + 5xy + 5y^{2} = t\) ![]() \((t\in Z)\) thì
\((t\in Z)\) thì
![]() \(A = (t - y^{2})( t + y^{2}) + y^{4} = t^{2} –y^{4} + y^{4} = t^{2} = (x^{2} + 5xy + 5y^{2})^{2}\)
\(A = (t - y^{2})( t + y^{2}) + y^{4} = t^{2} –y^{4} + y^{4} = t^{2} = (x^{2} + 5xy + 5y^{2})^{2}\)
Vì ![]() \(x,\ y,\ z\in Z\) nên
\(x,\ y,\ z\in Z\) nên ![]() \(x^2\in Z,\ 5xy\in Z,\ 5y^2\in Z\) ⇒
\(x^2\in Z,\ 5xy\in Z,\ 5y^2\in Z\) ⇒ ![]() \(x^2+5xy+5y^2\in Z\)
\(x^2+5xy+5y^2\in Z\)
Vậy A là số chính phương.
Bài 2: Chứng minh tích của 4 số tự nhiên liên tiếp cộng 1 luôn là số chính phương.
Gọi 4 số tự nhiên, liên tiêp đó là n, n + 1, n+ 2, n + 3 ![]() \(\left(n\in Z\right)\). Ta có
\(\left(n\in Z\right)\). Ta có
![]() \(n(n+1)(n+2)(n+3)+1\) =
\(n(n+1)(n+2)(n+3)+1\) = ![]() \(n.(n+3(n+1)(n+2)+1\)
\(n.(n+3(n+1)(n+2)+1\)
= ![]() \((n^2+3n)(n^2+3n+2)+1\) (*)
\((n^2+3n)(n^2+3n+2)+1\) (*)
Đặt ![]() \(n^2+3n=t\ (t\in N)\) thì
\(n^2+3n=t\ (t\in N)\) thì
(*) = ![]() \(t\ (t+2)+1\) =
\(t\ (t+2)+1\) = ![]() \(t^2+2t+1\) =
\(t^2+2t+1\) = ![]() \((t+1)^2\)
\((t+1)^2\)
= ![]() \((n^2+3n+1)^2\)
\((n^2+3n+1)^2\)
Vì ![]() \(n\in N\) nên
\(n\in N\) nên ![]() \(n^2+3n+1\in N\) Vậy
\(n^2+3n+1\in N\) Vậy ![]() \(n(n+1)(n+2)(n+3)+1\) là số chính phương.
\(n(n+1)(n+2)(n+3)+1\) là số chính phương.
Bài 3: Cho ![]() \(S=1.2.3+2.3.4+3.4.5+...+k(k+1)(k+2)\)
\(S=1.2.3+2.3.4+3.4.5+...+k(k+1)(k+2)\)
Chứng minh rằng ![]() \(4S+1\) là số chính phương.
\(4S+1\) là số chính phương.
Ta có
![]() \(k(k+1)(k+2)\)
\(k(k+1)(k+2)\)
= ![]() \(\frac{1}{4}k\ (k+1)(k+2).4\)
\(\frac{1}{4}k\ (k+1)(k+2).4\)
= ![]() \(\frac{1}{4}k(k+1)(k+2).[(k+3)-(k-1)]\)
\(\frac{1}{4}k(k+1)(k+2).[(k+3)-(k-1)]\)
= ![]() \(\frac{1}{4}k(k+1)(k+2)(k+3)-\frac{1}{4}k(k+1)(k+2)(k-1)\)
\(\frac{1}{4}k(k+1)(k+2)(k+3)-\frac{1}{4}k(k+1)(k+2)(k-1)\)
⇒ ![]() \(S=\frac{1}{4}.1.2.3.4-\frac{1}{4}.0.1.2.3+\frac{1}{4}.2.3.4.5-\frac{1}{4}.1.2.3.4+\dots+\frac{1}{4}k(k+1)(k+2)(k+3)-\frac{1}{4}\)
\(S=\frac{1}{4}.1.2.3.4-\frac{1}{4}.0.1.2.3+\frac{1}{4}.2.3.4.5-\frac{1}{4}.1.2.3.4+\dots+\frac{1}{4}k(k+1)(k+2)(k+3)-\frac{1}{4}\)
![]() \(k(k+1)(k+2)(k-1)\) =
\(k(k+1)(k+2)(k-1)\) = ![]() \(\frac{1}{4}k(k+1)(k+2)(k+3)\)
\(\frac{1}{4}k(k+1)(k+2)(k+3)\)
![]() \(4S+1=k(k+1)(k+2)(k+3)+1\)
\(4S+1=k(k+1)(k+2)(k+3)+1\)
Theo kết quả bài 2 ⇒ ![]() \(k(k+1)(k+2)(k+3)+1\) là số chính phương.
\(k(k+1)(k+2)(k+3)+1\) là số chính phương.
Bài 4: Cho dãy số 49; 4489; 444889; 44448889; …
Dãy số trên được xây dựng bằng cách thêm số 48 vào giữa số đứng trước nó. Chứng minh rằng tất cả các số của dãy trên đều là số chính phương.
 Ta có
Ta có
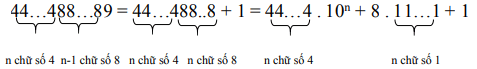
![]() \(=4\cdot\frac{10^n-1}{9}\cdot10^n+8\cdot\frac{10^n-1}{9}+1\)
\(=4\cdot\frac{10^n-1}{9}\cdot10^n+8\cdot\frac{10^n-1}{9}+1\)
![]() \(=\frac{4.10^{2n}-4.10^n+8.10^n-8+9}{9}=\frac{4.10^{2n}+4.10^n+1}{9}\)
\(=\frac{4.10^{2n}-4.10^n+8.10^n-8+9}{9}=\frac{4.10^{2n}+4.10^n+1}{9}\)
![]() \(=\left(\frac{2.10^n+1}{3}\right)\)
\(=\left(\frac{2.10^n+1}{3}\right)\)
Ta thấy  \(2.10^{n} +1=2\underbrace{00…0}_{n-1 \text{ chữ số }0} 1\) có tổng các chữ số chia hết cho 3 nên nó chia hết cho 3
\(2.10^{n} +1=2\underbrace{00…0}_{n-1 \text{ chữ số }0} 1\) có tổng các chữ số chia hết cho 3 nên nó chia hết cho 3
⇒ ![]() \(\left(\frac{2.10^n+1}{3}\right)\in Z\) hay các số có dạng 44…488…89 là số chính phương.
\(\left(\frac{2.10^n+1}{3}\right)\in Z\) hay các số có dạng 44…488…89 là số chính phương.
Bài 5: Chứng minh rằng các số sau đây là số chính phương:
 \(A = \underbrace{11…1}_{2n\text{ chữ số }1} + \underbrace{44…4}_{n\text{ chữ số }4} + 1\)
\(A = \underbrace{11…1}_{2n\text{ chữ số }1} + \underbrace{44…4}_{n\text{ chữ số }4} + 1\)
 \(B = \underbrace{11…1}_{2n\text{ chữ số }1} + \underbrace{11…1}_{n+1\text{ chữ số }1} + \underbrace{66…6}_{n\text{ chữ số }6} + 8\)
\(B = \underbrace{11…1}_{2n\text{ chữ số }1} + \underbrace{11…1}_{n+1\text{ chữ số }1} + \underbrace{66…6}_{n\text{ chữ số }6} + 8\)
 \(C = \underbrace{44…4}_{2n\text{ chữ số }4} + \underbrace{22…2}_{n+1\text{ chữ số }2} + \underbrace{88…8}_{n\text{ chữ số }8} + 7\)
\(C = \underbrace{44…4}_{2n\text{ chữ số }4} + \underbrace{22…2}_{n+1\text{ chữ số }2} + \underbrace{88…8}_{n\text{ chữ số }8} + 7\)
Kết quả:  \(A=\left(\frac{10^n+2}{3}\right)^2\);
\(A=\left(\frac{10^n+2}{3}\right)^2\);  \(B=\left(\frac{10^n+8}{3}\right)^2\);
\(B=\left(\frac{10^n+8}{3}\right)^2\);  \(C=\left(\frac{2.10^n+7}{3}\right)^2\)
\(C=\left(\frac{2.10^n+7}{3}\right)^2\)
Bài 6: Chứng minh rằng các số sau là số chính phương:
a)  \(A = 224\underbrace{99…9}_{n-2\text{ chữ số }9} 1\underbrace{00…0}_{n\text{ chữ số }0} 9\)
\(A = 224\underbrace{99…9}_{n-2\text{ chữ số }9} 1\underbrace{00…0}_{n\text{ chữ số }0} 9\)
b)  \(B = \underbrace{11...1}_{n\text{ chữ số }1} \underbrace{55...5}_{n-1\text{ chữ số }5}6\)
\(B = \underbrace{11...1}_{n\text{ chữ số }1} \underbrace{55...5}_{n-1\text{ chữ số }5}6\)
a) ![]() \(A=224.10^{2n}+99\dots9.10^{n+2}+10^{n+1}+9\)
\(A=224.10^{2n}+99\dots9.10^{n+2}+10^{n+1}+9\)
![]() \(=224.10^{2n}+(10^{n-2}-1).10^{n+2}+10^{n+1}+9\)
\(=224.10^{2n}+(10^{n-2}-1).10^{n+2}+10^{n+1}+9\)
![]() \(=224.10^{2n}+10^{2n}-10^{n+2}+10^{n+1}+9\)
\(=224.10^{2n}+10^{2n}-10^{n+2}+10^{n+1}+9\)
![]() \(=225.10^{2n}-90.10^n+9\)
\(=225.10^{2n}-90.10^n+9\)
![]() \(=(15.10^n-3)^2\)
\(=(15.10^n-3)^2\)
⇒ A là số chính phương.
b) 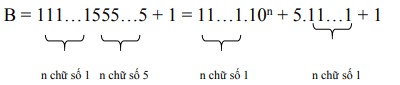
![]() \(=\ \frac{10^n-1}{9}.10^n+5.\frac{10^n-1}{9}+1\)
\(=\ \frac{10^n-1}{9}.10^n+5.\frac{10^n-1}{9}+1\)![]() \(=\frac{10^{2n}-10^n+5.10^n-5+9}{9}\)
\(=\frac{10^{2n}-10^n+5.10^n-5+9}{9}\)
 \(=\frac{10^{2n}+4.10^n+4}{9}=\left(\frac{10^n+2}{3}\right)^{^2}\)là số chính phương (điều phải chứng minh)
\(=\frac{10^{2n}+4.10^n+4}{9}=\left(\frac{10^n+2}{3}\right)^{^2}\)là số chính phương (điều phải chứng minh)
.............................................
Download file tài liệu để xem thêm nội dung chi tiết Bài tập toán lớp 6
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:












 Toán 6 Kết nối tri thức
Toán 6 Kết nối tri thức
 Toán 6 Chân trời sáng tạo
Toán 6 Chân trời sáng tạo
 Toán 6 Cánh Diều
Toán 6 Cánh Diều
 Soạn văn 6 Chân trời sáng tạo
Soạn văn 6 Chân trời sáng tạo
 Soạn văn 6 Cánh Diều
Soạn văn 6 Cánh Diều
 Soạn Văn 6 Kết nối tri thức
Soạn Văn 6 Kết nối tri thức
 Tiếng Anh 6 Global Success
Tiếng Anh 6 Global Success
 Tiếng Anh 6 Friends Plus
Tiếng Anh 6 Friends Plus
 Tiếng Anh 6 Explore English
Tiếng Anh 6 Explore English
 Khoa học tự nhiên 6 CTST
Khoa học tự nhiên 6 CTST









