Eballsviet.com
Học tập Lớp 11 Toán 11

Bài tập nâng cao giới hạn của dãy số Tài liệu ôn tập chương 3 môn Toán lớp 11

Giới thiệu Tải về Bình luận

Mời quý thầy cô cùng các bạn học sinh lớp 11 cùng tham khảo tài liệu Bài tập nâng cao giới hạn của dãy số được Eballsviet.com đăng tải ngay sau đây.

Bài tập nâng cao giới hạn của dãy số là tài liệu cực kì hữu ích, gồm 14 trang hướng dẫn giải các bài tập nâng cao giới hạn của dãy số được chọn lọc từ các đề thi HSG cấp tỉnh, cấp quốc gia. Hi vọng tài liệu sẽ giúp các bạn học sinh lớp 11 bổ sung kiến thức về phần dãy số trong các kì thi học sinh giỏi và tài liệu tham khảo bổ ích cho bạn đọc. Mời các bạn cùng tham khảo.

Bài tập nâng cao giới hạn của dãy số

Giới hạn của dãy số
Nguyễn Minh Tuấn - GV trường THPT Chuyên QB
NỘI DUNG
I) Phương pháp sử dụng định nghĩa giới hạn dãy số
1. Kiến thức sử dụng:
Định nghĩa:
*
lim 0, :
n n
u L N N n N u L
Sử dụng:
- Tiêu chuẩn Cô-si: Dãy {x
n
} có giới hạn hữu hạn khi và chỉ khi với mọi > 0,
tồn tại số tự nhiên N sao cho với mọi m, n N ta có |x
m
– x
n
| < .
- Nguyên lý ánh xạ co: Nếu với mọi x, y ta có |f(x) – f(y)| q|x-y| với q là
hằng số 0 < q < 1 và {x
n
} bị chặn thì {x
n
} hội tụ. Đặc biệt nếu |f’(x)| q < 1 thì ta
luôn có điều này.
Ý tưởng chính: Đánh giá
1
; 1
n n
u L q u L q
và
1 1
; 1
n n n n
u u q u u q
Phương pháp này thường được dùng khi ta thấy dãy số không tăng, không giảm.
2. Các ví dụ:
Bài 1: (Đề thi HSG Quảng Bình) Cho dãy số
1
1
u
và
2
1
1
1
2
n n
u u
. Tìm giới hạn dãy
số?
HD: Chứng minh:
1 0
n
u
Giải phương trình
2
1
1 1 3
2
x x x a
Xét
2 2
1 3
1 1
2 2 2 2
n
n n n n
u a
u a u a u a u a
Suy ra
lim 1 3
n
u
Bài 2: (Đề dự bị VMO 2008) Cho số thực a và dãy số thực
( )
n
u
xác định bởi:
1
u a
và u
n+1
= ln(3+cosu
n
+ sinu
n
) – 2008 với mọi n = 1, 2, 3, …
Chứng minh rằng dãy số (u
n
)có giới hạn hữu hạn.
HD: Đặt f(x) = ln(3+sinx+cosx) – 2008 thì
cos sin
'( )
3 sin cos
x x
f x
x x
Từ đó, sử dụng đánh giá
| cos sin | 2, | sin cos | 2
x x x x
ta suy ra
.1
23
2
|)('|
qxf
Áp dụng định lý Lagrange với m > n N, ta có
|u
m
– u
n
| = |f(u
m-1
) – f(u
n-1
)|
q|u
m-1
-u
n-1
|
…
q
n-1
|u
m-n+1
– u
1
|.
Do dãy (u
n
) bị chặn và q < 1 nên dãy (x
n
) thoả mãn điều kiện Cauchy nên có giới hạn
hữu hạn.
Bài tập nâng cao giới hạn của dãy số
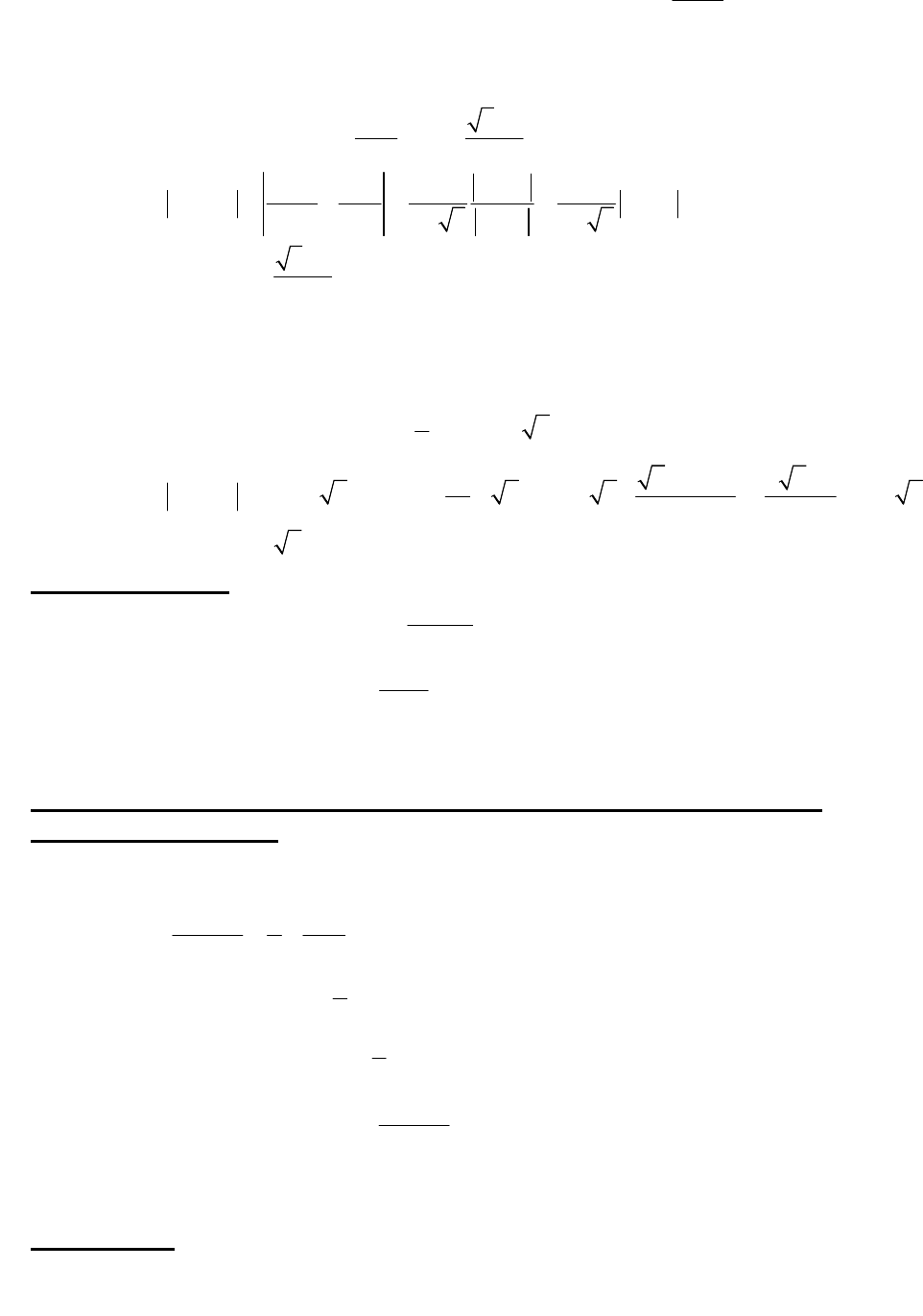
Giới hạn của dãy số
Nguyễn Minh Tuấn - GV trường THPT Chuyên QB
Bài 3: (Đề thi vô địch Nga 1982) Cho dãy số
1
1
u
và
1
1
1
n
n
u
u
. Tìm giới hạn dãy
số?
HD: Chứng minh:
0 1
n
u
Giải phương trình
1 5 1
1 2
x x a
x
Xét
1
1 1 2 2
1 1 1
1 5 1 5
n
n n
n n
u a
u a u a
u a u
Suy ra
5 1
lim
2
n
u a
Bài 4: Cho dãy số (u
n
) định bởi u
1
(1, 2) và u
n+1
= 1 + u
n
– u
n
2
/2. Chứng minh
rằng (u
n
) có giới hạn hữu hạn và tìm giới hạn đó.
HD: Chứng minh: rằng 1 < u
n
< 3/2
Giải phương trình
2
1
1 2
2
x x x x a
Xét
2
1 1
2 1 2 2 1
| 2 | |1 2 | | 2 || | | || 2 |
2 2 4
n n
n n n n n
u u
u a u u u u
Suy ra
lim 2
n
u
3. Bài tập tự giải:
Bài 1: Cho dãy số
1
2012
u
và
1
1
4 3
n
n
u
u
. Tìm giới hạn dãy số?
Bài 2: Cho dãy số
1
u a
và
2 2 2
1
2012
ln 2012 2012
3
n n
u u
.Chứng minh dã số có giới
hạn.
II) Phương pháp sử dụng công thức, tính chất của các dãy số đặc biệt
1. Kiến thức sử dụng:
- Tính chất của các dãy số là cấp số cộng, cấp số nhân
- Các công thức đối với các dãy số quen thuộc:
1 1 1
( 1) 1
n n n n
1
1 2 3 ... ( 1)
2
n n n
2 2 2 2
1
1 2 3 ... ( 1)(2 1)
6
n n n n
2
3 3 3 3
( 1)
1 2 3 ...
2
n n
n
Ý tưởng chính: Đưa các dãy số về các dãy số quen thuộc
2. Các ví dụ:
Giới hạn của dãy số
Nguyễn Minh Tuấn - GV trường THPT Chuyên QB
Bài 1: Cho dãy số
1 1 1
...
1.2 2.3 ( 1)
n
u
nn
.Tìm giới hạn dãy số?
HD:
1 1 1 1 1 1 1
... 1
1 2 2 3 1 1
n
u
n n n
Suy ra
lim 1
n
u
Bài 2: Cho dãy số
2
2 2 2
2
2 2 2
1 3 5 .... 2 1
2 4 6 .... 2
n
n
u
n
.Tìm giới hạn dãy số?
HD:
2
2 2 2
2
2 2 2
2 (2 1)(4 1)
1 2 3 .... 2
(4 1)
6
1
( 1)(2 1)
2( 1)
2 4 6 .... 2
4.
6
n
n n n
n
n
u
n n n
n
n
Suy ra
lim 1
n
u
.
Bài 3: Cho dãy số
1
5
u
và
1
5 4
2
n
n
n
u
u
u
. Tìm giới hạn dãy số?
HD: Chứng minh:
4
n
u
Ta có:
1
1
4
1 6
4 1
2 4 4
n
n
n n n
u
u
u u u
Xét
1 1 5
4
4 5 6 1
n n
n
n
x u
u
Suy ra
lim 4
n
u
Bài 4: Cho dãy số
1
2
3
u
và
1
2(2 1) 1
n
n
n
u
u
n u
. Tìm giới hạn dãy số
1
n
n n
i
x u
?
HD: Đặt
1 (2 1)(2 1) 1 1
2 2 1 2 1
n n n
n
n n
v v u
u n n
Suy ra
lim 1
n
x
Bài 5: Cho dãy số
1
1
u
và
2
1
(0 1)
n
n n
u u a a
. Tìm giới hạn dãy số?
HD: Chứng minh:
2 2 2 2 2 2 1
1 2 3
1; 1 ; 1 ;...; 1 ...
n
n
u u a u a a u a a a
Suy ra:
1
1
n
n
a
u
a
Vậy
1
lim
1
n
u
a
Bài 6: Cho dãy số
1
2011
u
và
2
1 1
n n n
u n u u
. Tìm giới hạn dãy số?
HD: Ta có:
2
1
1
2
1
0
n
n n
n u
u u
n
Mặt khác:
1 2 1
2 2 2
( 1)( 1) ( 1)( 1)( 2) 1 1
... 2011
( 1) 2 2
n n n
n n n n n n n n
u u u u
n n n n n
Vậy
2011
lim
2
n
u
Liên kết tải về
Tìm thêm: Toán 11

Có thể bạn quan tâm

Xem thêm
Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!
Số điện thoại này đã được xác thực!
Bạn có thể dùng Sđt này đăng nhập tại đây!
Lỗi gửi SMS, liên hệ Admin
Sắp xếp theo
👨
Đóng
Chỉ thành viên Download Pro tải được nội dung này! Download Pro - Tải nhanh, website không quảng cáo! Tìm hiểu thêm
Mua Download Pro 79.000đ

Mới nhất trong tuần