1. Chu kì của con lắc lò xo là: ![]() \(T=2\pi\sqrt{\frac{m}{k}}\)
\(T=2\pi\sqrt{\frac{m}{k}}\)
2. Thực hiện bằng đồng hồ bấm giờ thấy kết quả giống với công thức tính với sai số nhỏ hơn 0,01s
Giải Vật lý 11 trang 20, 21, 22, 23 Kết nối tri thức với cuộc sống giúp các em học sinh lớp 11 có thêm nhiều gợi ý tham khảo để biết cách trả lời các câu hỏi bài học bài 5: Động năng - Thế năng -Sự chuyển hóa năng lượng trong dao động điều hòa của Chương 1: Dao động
Giải Lý 11 Kết nối tri thức bài 5 các em sẽ hiểu được kiến thức lý thuyết về động năng, thế năng và biết cách trả lời toàn bộ các câu hỏi trang 20→23 trong sách giáo khoa Vật lí 11. Đồng thời qua đó giúp quý thầy cô tham khảo để soạn giáo án cho học sinh của mình.
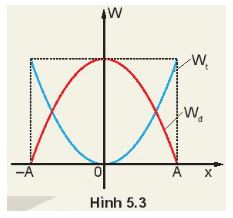
Hình 5.3 là đồ thị động năng và thế năng của một vật dao động điều hòa li độ. Hãy phân tích sự chuyển hóa giữa động năng và thế năng bằng đồ thị.
Gợi ý đáp án
Khi vật di chuyển từ biên âm đến vị trí cân bằng thì thế năng giảm động năng tăng và ngược lại
Khi vật đi chuyển từ vị trí cân bằng đến biên dương thì thế năng tăng động năng giảm và ngược lại
Vật đạt động năng cực đại khi ở vị trí cân bằng và cực tiểu khi ở vị trí biên còn thế năng thì ngược lại
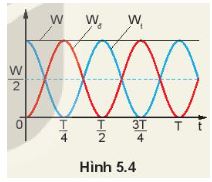
Hình 5.4 là đồ thị động năng và thế năng của một vật dao động điều hòa theo thời gian.
a) Động năng và thế năng của vật thay đổi như thế nào trong các khoảng thời gian: từ 0 đến T/4, từ T/4 đến T/2, từ T/2 đến 3T/4, từ 3T/4 đến T
b) Tại các thời điểm: t = 0; t = T/8; t = 3T/8, động năng và thế năng của vật có giá trị như thế nào (tính theo W). Nghiệm lại để thấy ở mỗi thời điểm đó Wđ + Wt = W.
Gợi ý đáp án
a) Từ 0 đến T/4: Wđ tăng từ 0 đến giá trị lớn nhất tại T/4, Wt giảm từ giá trị lớn nhất về 0 tại T/4
Từ T/4 đến T/2: Wđ giảm từ giá trị lớn nhất về 0 tại T/2, Wt tăng từ 0 đến giá trị lớn nhất tại T/2
Từ T/2 đến 3T/4: Wđ tăng từ 0 đạt giá trị lớn nhất tại 3T/4 Wt giảm từ giá trị lớn nhất về 0 tại 3T/4
Từ 3T/4 đến T: Wđ giảm từ giá trị lớn nhất về 0 tại T, Wt tăng từ 0 đến giá trị lớn nhất tại T
b) Tại thời điểm t = 0: Wđ = 0, Wt = W
Tại thời điểm t = T/8: Wđ = Wt = W/2
Tại thời điểm t = T/4: Wđ = W, Wt = 0
Tại thời điểm t = 3T/8: Wđ= Wt = W/2
→ ở mỗi thời điểm trên ta đều có: Wđ + Wt = W.
Làm thí nghiệm để xác nhận rằng khi góc lệch α0 ≤ 10∘ thì chu kì của con lắc đơn gần như không phụ thuộc vào biên độ dao động.
Gợi ý đáp án
Vị trí của con lắc đơn được xác định bằng li độ dài s hay li độ góc ![]() \(\alpha\)
\(\alpha\)
Thế năng của con lắc đơn là thế năng trọng trường.
Chọn mốc tính thế năng ở vị trí cân bằng thì thế năng của con lắc ở li độ góc ![]() \(\alpha\) là:
\(\alpha\) là: ![]() \(W_{t}=mgl(1-cos\alpha)\)
\(W_{t}=mgl(1-cos\alpha)\)
mà ![]() \((1-cos\alpha)=2sin^{2}\frac{\alpha}{2}\) với
\((1-cos\alpha)=2sin^{2}\frac{\alpha}{2}\) với ![]() \(\alpha _{0} \leq 10^{\circ} thì sin\frac{\alpha}{2}\approx \frac{\alpha}{2}\) (
\(\alpha _{0} \leq 10^{\circ} thì sin\frac{\alpha}{2}\approx \frac{\alpha}{2}\) ( ![]() \(\alpha\) tính theo rad)
\(\alpha\) tính theo rad)
khi đó ![]() \(W_{t}=mgl\frac{\alpha ^{2}}{2}\) với
\(W_{t}=mgl\frac{\alpha ^{2}}{2}\) với ![]() \(\alpha=\frac{s}{l}\) suy ra:
\(\alpha=\frac{s}{l}\) suy ra: ![]() \(W_{t}=mgl\frac{s^{2}}{2l^{2}}=\frac{1}{2}m\frac{g}{l}s^{2}\)
\(W_{t}=mgl\frac{s^{2}}{2l^{2}}=\frac{1}{2}m\frac{g}{l}s^{2}\)
Tại vị trí biên độ có Wt = W nên ta có  \(\frac{1}{2}m\frac{g}{l}s^{2}=\frac{1}{2}m\omega ^{2}A^{2}
\rightarrow \omega = \sqrt{\frac{g}{l}} \rightarrow T=2\pi\sqrt{\frac{l}{g}}\)
\(\frac{1}{2}m\frac{g}{l}s^{2}=\frac{1}{2}m\omega ^{2}A^{2}
\rightarrow \omega = \sqrt{\frac{g}{l}} \rightarrow T=2\pi\sqrt{\frac{l}{g}}\)
vậy với góc lệch ![]() \(\alpha _{0} \leq 10^{\circ}\) thì chu kì của con lắc đơn gần như không phụ thuộc vào biên độ dao động.
\(\alpha _{0} \leq 10^{\circ}\) thì chu kì của con lắc đơn gần như không phụ thuộc vào biên độ dao động.
Một con lắc lò xo có độ cứng k và vật nặng có khối lượng m.
1. Tính chu kì
2. Đo chu kì T bằng đồng hồ. So sánh kết quả tính ở câu 1
Gợi ý đáp án
1. Chu kì của con lắc lò xo là: ![]() \(T=2\pi\sqrt{\frac{m}{k}}\)
\(T=2\pi\sqrt{\frac{m}{k}}\)
2. Thực hiện bằng đồng hồ bấm giờ thấy kết quả giống với công thức tính với sai số nhỏ hơn 0,01s
a) Vận tốc cực đại của vật.
b) Động năng cực đại của vật.
c) Thế năng cực đại của con lắc.
d) Độ cứng k của lò xo
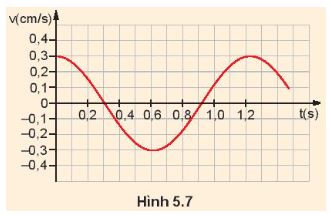
Gợi ý đáp án
Từ đồ thị ta có T = 1,2s ![]() \(\rightarrow \omega = \frac{2\pi}{T}=\frac{5}{3}\) (rad/s)
\(\rightarrow \omega = \frac{2\pi}{T}=\frac{5}{3}\) (rad/s)
a) Vận tốc cực đại của vật vmax= 0,3 cm/s= 0,003 m/s = ![]() \(\omega A \rightarrow A\) = 0.0018 (m)
\(\omega A \rightarrow A\) = 0.0018 (m)
b) Động năng cực đại của vật là Wđmax = ![]() \(\frac{1}{2}m\omega ^{2} A^{2}\) =
\(\frac{1}{2}m\omega ^{2} A^{2}\) = ![]() \(4,5.10^{-6}\) (J)
\(4,5.10^{-6}\) (J)
c) Theo định luật bảo toàn cơ năng ta có Wt max = W đmax = ![]() \(4,5.10^{-6}\) (J)
\(4,5.10^{-6}\) (J)
d) Độ cứng k của lò xo tính theo công thức: ![]() \(T=2\pi\sqrt{\frac{m}{k}} \rightarrow k \approx 11\) (N/m)
\(T=2\pi\sqrt{\frac{m}{k}} \rightarrow k \approx 11\) (N/m)
Một con lắc lò xo có độ cứng k = 100 N/m, vật nặng có khối lượng m = 200 g, dao động điều hòa với biên độ A = 5 cm.
a) Xác định li độ của vật tại thời điểm động năng của vật bằng 3 lần thế năng của con lắc.
b) Xác định tốc độ của vật khi qua vị trí cân bằng.
c) Xác định thế năng của con lắc khi vật có li độ x = -2,5 cm.
Gợi ý đáp án
Ta có:
Độ cứng k = 100 N/m
Khối lượng m = 200 g = 0,2 kg
Biên độ A = 5 cm = 0,05 m
a) Wđ = 3 Wt
Theo định luật bảo toàn cơ năng W = W đ + W t = 4Wt
![]() \(\rightarrow \frac{1}{2}m\omega ^{2}A^{2} = 4 \frac{1}{2}m\omega ^{2}x^{2} \rightarrow x = \pm 2,5\) (cm)
\(\rightarrow \frac{1}{2}m\omega ^{2}A^{2} = 4 \frac{1}{2}m\omega ^{2}x^{2} \rightarrow x = \pm 2,5\) (cm)
b) Tần số góc ![]() \(\omega = \sqrt{\frac{k}{m}} = 10\sqrt{5}\) (rad/s)
\(\omega = \sqrt{\frac{k}{m}} = 10\sqrt{5}\) (rad/s)
Khi vật đi qua vị trí cân bằng vật có tốc độ lớn nhất v = ![]() \(\omega A\) =
\(\omega A\) = ![]() \(0,05.10\sqrt{5}\) =
\(0,05.10\sqrt{5}\) = ![]() \(\frac{\sqrt{5}}{2}\) (m/s)
\(\frac{\sqrt{5}}{2}\) (m/s)
c) ![]() \(Wt1 = \frac{1}{2}m\omega ^{2}x^{2}= 1562,5\) (s)
\(Wt1 = \frac{1}{2}m\omega ^{2}x^{2}= 1562,5\) (s)
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây: