Công thức thấu kính Công thức thấu kính hội tụ, thấu kính phân kỳ
Công thức thấu kính bao gồm toàn bộ kiến thức lý thuyết về công thức tính thấu kính hội tụ, công thức tính thấu kính phân kì. Qua đó giúp các bạn học sinh có thêm nhiều tư liệu học tập củng cố kiến thức biết cách vận dụng vào giải bài tập vật lí.

Thấu kính là một trong những kiến thức trọng tâm các em sẽ được học trong chương trình lớp 9 và lớp 11. Thấu kính là một dụng cụ quang học dùng để hội tụ hay phân kỳ những chùm ánh sáng khác nhau. Việc nắm vững công thức thấu kính rất quan trọng giúp các bạn học sinh nhanh chóng biết cách vận dụng vào giải bài tập liên quan đến thấu kính. Bên cạnh công thức thấu kính các bạn xem thêm công thức tính tụ điện.
Công thức thấu kính
1. Thấu kính hội tụ là gì?
Thấu kính hội tụ được giới hạn bởi 2 mặt cong hoặc một mặt cong và một mặt phẳng có phần rìa phía ngoài mỏng. Chùm sáng song song đi qua thấu kính rìa mỏng tụ lại một điểm nên thấu kính rìa mỏng được gọi là thấu kính hội tụ
2. Thấu kính phân kì là gì?
Thấu kính phân kì là loại thấu kính được giới hạn bởi hai mặt cong hoặc một mặt phẳng và một mặt cong phía rìa bên ngoài thấu kính dày. Chùm sáng song song đi qua thấu kính rìa mỏng bị phân tách ra theo các hướng khác nhau nên thấu kính rìa dày còn được gọi là thấu kính phân kỳ.
3. Công thức liên hệ giữa vị trí của vật, vị trí của ảnh và tiêu cự của thấu kính
![]() \(\frac{1}{f}=\frac{1}{d}+\frac{1}{d'}\)
\(\frac{1}{f}=\frac{1}{d}+\frac{1}{d'}\)
a. Qui ước dấu:
- Thấu kính hội tụ: f > 0
- Thấu kính phân kỳ: f < 0
- ảnh là thật: d’ > 0
- ảnh là ảo: d’ < 0
- vật là thật: d > 0
– Tiêu diện:
- Tiêu diện vật: mặt phẳng vuông góc với trục chính tại tiêu điểm vật
- Tiêu diện ảnh: mặt phẳng vuông góc với trục chính tại tiêu điểm ảnh
– Tiêu điểm phụ:
- Các tiêu điểm vật phụ ở trên mặt phẳng tiêu diện vật vuông góc với trục chính tại F.
- Các tiêu điểm ảnh phụ ở trên mặt phẳng tiêu diện ảnh vuông góc với trục chính tại F’.
b. Công thức số phóng đại của thấu kính
 \(\begin{aligned}
&|k|=\frac{A^{\prime} B^{\prime}}{A B} \\
&=\frac{-d^{\prime}}{d}=\frac{f}{f-d}
\end{aligned}\)
\(\begin{aligned}
&|k|=\frac{A^{\prime} B^{\prime}}{A B} \\
&=\frac{-d^{\prime}}{d}=\frac{f}{f-d}
\end{aligned}\)
Qui ước dấu:
+ k > 0: ảnh và vật cùng chiều
+ k < 0: ảnh và vật là ngược chiều
c. Công thức tính độ tụ của thấu kính
![]() \(D=\frac{1}{f}=(n-1)\left(\frac{1}{R_{1}}+\frac{1}{R_{2}}\right)\)
\(D=\frac{1}{f}=(n-1)\left(\frac{1}{R_{1}}+\frac{1}{R_{2}}\right)\)
Trong đó:
- n: chiết suất của chất làm thấu kính
- R1; R2: bán kính của các mặt cong (R = ∞ cho trường hợp mặt phẳng) (m)
- D: độ tụ của thấu kính (dp đọc là điốp)
- f: tiêu cự của thấu kính (m)
4. Chứng minh công thức thấu kính hội tụ
– Xét trường hợp vật sáng AB đặt vuông góc với trục chính của thấu kính hội tụ.
- d = OA: khoảng cách từ vị trí của vật đến thấu kính
- d’ = OA’: khoảng cách từ vị trí của ảnh đến thấu kính
- f = OF = OF’: tiêu cự của thấu kính
- A’B’: chiều cao của ảnh
- AB: chiều cao của vật
a.Trường hợp vật thật qua thấu kính hội tụ cho ảnh thật
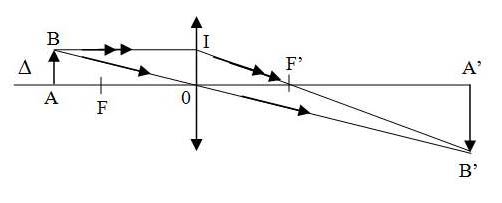
Tam giác A'B'C' đồng dạng với tam giác ABO
![]() \(\frac{A^{\prime} B^{\prime}}{A B}=\frac{A^{\prime} O}{A O}=\frac{d^{\prime}}{d} \text { (1) }\)
\(\frac{A^{\prime} B^{\prime}}{A B}=\frac{A^{\prime} O}{A O}=\frac{d^{\prime}}{d} \text { (1) }\)
Tam giác A'B'F' đồng dạng với tam giác OIF
![]() \(\frac{A^{\prime} B^{\prime}}{O I}=\frac{A^{\prime} F^{\prime}}{O F^{\prime}}=\frac{O A^{\prime}-O F^{\prime}}{O F^{\prime}}=\frac{d^{\prime}-f}{f}(2)\)
\(\frac{A^{\prime} B^{\prime}}{O I}=\frac{A^{\prime} F^{\prime}}{O F^{\prime}}=\frac{O A^{\prime}-O F^{\prime}}{O F^{\prime}}=\frac{d^{\prime}-f}{f}(2)\)
Từ (1) và (2)![]() \(=>\frac{d^{\prime}}{d}=\frac{d^{\prime}-f}{f} \Rightarrow \frac{1}{f}=\frac{1}{d}+\frac{1}{d^{\prime}}\)
\(=>\frac{d^{\prime}}{d}=\frac{d^{\prime}-f}{f} \Rightarrow \frac{1}{f}=\frac{1}{d}+\frac{1}{d^{\prime}}\)
b. Trường hợp vật thật qua thấu kính hội tụ cho ảnh ảo
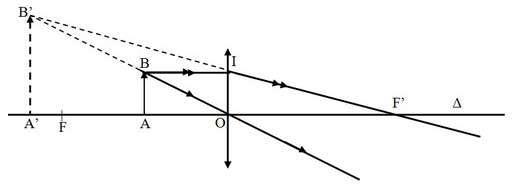
![]() \(\triangle \mathrm{ABO}\) đồng dạng với
\(\triangle \mathrm{ABO}\) đồng dạng với ![]() \(\triangle \mathrm{A}^{\prime} \mathrm{B}^{\prime} \mathrm{O}=>\)
\(\triangle \mathrm{A}^{\prime} \mathrm{B}^{\prime} \mathrm{O}=>\)
![]() \(\frac{A^{\prime} B^{\prime}}{A B}=\frac{A^{\prime} O}{A O}=\frac{d^{\prime}}{d} \text { (1) }\)
\(\frac{A^{\prime} B^{\prime}}{A B}=\frac{A^{\prime} O}{A O}=\frac{d^{\prime}}{d} \text { (1) }\)
![]() \(\triangle \mathrm{OIF} \mathrm{F}^{\prime}\) đồng dạng với
\(\triangle \mathrm{OIF} \mathrm{F}^{\prime}\) đồng dạng với ![]() \(\triangle \mathrm{A}^{\prime} \mathrm{B}^{\prime} \mathrm{F}^{\prime}=>\)
\(\triangle \mathrm{A}^{\prime} \mathrm{B}^{\prime} \mathrm{F}^{\prime}=>\)
![]() \(\frac{A^{\prime} B^{\prime}}{O I}=\frac{A^{\prime} B^{\prime}}{A B}=\frac{A^{\prime} F^{\prime}}{O F^{\prime}}=\frac{O A^{\prime}+O F^{\prime}}{O F^{\prime}}=\frac{d^{\prime}+f}{f}(2)\)
\(\frac{A^{\prime} B^{\prime}}{O I}=\frac{A^{\prime} B^{\prime}}{A B}=\frac{A^{\prime} F^{\prime}}{O F^{\prime}}=\frac{O A^{\prime}+O F^{\prime}}{O F^{\prime}}=\frac{d^{\prime}+f}{f}(2)\)
Từ (1) và (2) ![]() \(\Rightarrow \frac{d^{\prime}}{d}=\frac{d^{\prime}+f}{f} \Rightarrow \frac{1}{f}=\frac{1}{d}-\frac{1}{d^{\prime}}\)
\(\Rightarrow \frac{d^{\prime}}{d}=\frac{d^{\prime}+f}{f} \Rightarrow \frac{1}{f}=\frac{1}{d}-\frac{1}{d^{\prime}}\)
c. Chứng minh công thức thấu kính phân kỳ
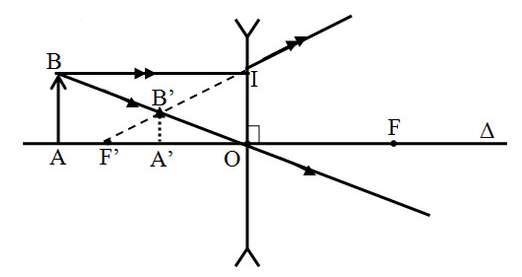
![]() \(\triangle \mathrm{ABO}\) đồng dạng với
\(\triangle \mathrm{ABO}\) đồng dạng với ![]() \(\triangle \mathrm{A}^{\prime} \mathrm{B}^{\prime} \mathrm{O}=>\)
\(\triangle \mathrm{A}^{\prime} \mathrm{B}^{\prime} \mathrm{O}=>\)
![]() \(\frac{A^{\prime} B^{\prime}}{A B}=\frac{A^{\prime} O}{A O}=\frac{d^{\prime}}{d}(1)\)
\(\frac{A^{\prime} B^{\prime}}{A B}=\frac{A^{\prime} O}{A O}=\frac{d^{\prime}}{d}(1)\)
![]() \(\triangle \mathrm{OIF} \mathrm{F}^{\prime}\) đồng dạng với
\(\triangle \mathrm{OIF} \mathrm{F}^{\prime}\) đồng dạng với ![]() \(\triangle \mathrm{A}^{\prime} \mathrm{B}^{\prime} \mathrm{F}^{\prime} và (\mathrm{Ol}=\mathrm{AB})=\)
\(\triangle \mathrm{A}^{\prime} \mathrm{B}^{\prime} \mathrm{F}^{\prime} và (\mathrm{Ol}=\mathrm{AB})=\)![]() \(\frac{A^{\prime} B^{\prime}}{A B}=\frac{A^{\prime} F^{\prime}}{O F^{\prime}}=\frac{O F^{\prime}-O A^{\prime}}{O F^{\prime}}=\frac{f-d^{\prime}}{f} \text { (2) }\)
\(\frac{A^{\prime} B^{\prime}}{A B}=\frac{A^{\prime} F^{\prime}}{O F^{\prime}}=\frac{O F^{\prime}-O A^{\prime}}{O F^{\prime}}=\frac{f-d^{\prime}}{f} \text { (2) }\)
Từ (1) và (2)![]() \(=>\frac{d^{\prime}}{d}=\frac{f-d^{\prime}}{f} \Rightarrow \frac{1}{f}=\frac{1}{d^{\prime}}-\frac{1}{d}\)
\(=>\frac{d^{\prime}}{d}=\frac{f-d^{\prime}}{f} \Rightarrow \frac{1}{f}=\frac{1}{d^{\prime}}-\frac{1}{d}\)
5. Đặc điểm của thấu kính
- Tiêu điểm ảnh chính: Chùm tia sáng tới thấu kính song song với trục chính sẽ tạo ra một tiêu điểm ảnh chính, được gọi là tiêu điểm ảnh chính hoặc tiêu điểm ảnh thật. Tiêu điểm ảnh chính của thấu kính hội tụ là thực sự, trong khi tiêu điểm ảnh chính của thấu kính phân kỳ là ảo.
- Tương quan giữa tiêu điểm vật và tiêu điểm ảnh: Tiêu điểm vật và tiêu điểm ảnh của thấu kính nằm ở hai bên của thấu kính và nối với nhau thông qua quang tâm.
- Tiêu diện vật và tiêu diện ảnh: Mặt phẳng vuông góc với trục chính tại tiêu điểm vật được gọi là tiêu diện vật. Mặt phẳng vuông góc với trục chính tại tiêu điểm ảnh được gọi là tiêu diện ảnh. Điểm cắt của một trục phụ bất kỳ với tiêu diện vật hoặc tiêu diện ảnh được gọi là tiêu điểm vật phụ hoặc tiêu điểm ảnh phụ.
- Quy luật giao điểm của tia: Chùm tia sáng tới song song với một trục phụ sẽ giao điểm tại tiêu điểm ảnh phụ của nó. Điều này có nghĩa là các tia ló hoặc các đường kéo dài của tia ló sẽ đi qua tiêu điểm ảnh phụ, tức là điểm giao của trục phụ song song với tia tới và tiêu diện ảnh.
6. Ứng dụng của thấu kính
- Khắc phục các tật của mặt (cận thị, viễn thị, lão thị)
- Dùng để chế tạo kính lúp
- Dùng để chế tạo kính hiển vi
- Dùng để chế tạo kính thiên văn, ống nhòm
- Dùng trong ống kính của máy ảnh, camera
- Sử dụng trong các máy phân tích quang phổ
7. Bài tập về thấu kính
Bài 1: Cho một thấu kính hội tụ có tiêu cự 30 cm. Vật sáng AB dài 3 cm đặt song song với trục chính của thấu kính và cách trục chính một khoảng h, điểm B ở cách thấu kính một khoảng dB = 15cm.
a) Dựng ảnh A’B’ của AB qua thấu kính. Nhận xét tính chất của ảnh A’B’ vừa dựng.
b) Tính độ dài ảnh A’B’ khi h = 10 √3cm.
Bài 2
Một vật sáng AB có dạng mũi tên đặt vuông góc trục chính của thấu kính phân kỳ, cho ảnh cao 3,6 cm và cách thấu kính 6 cm. Thấu kính có tiêu cự 15 cm. Xác định kích thước và vị trí của vật. Vẽ hình.
Bài 3
Một vật sáng AB có dạng mũi tên cao 6 cm đặt vuông góc trục chính của thấu kính hội tụ, cách thấu kính 15cm. Thấu kính có tiêu cự 10 cm.
a) Dựng ảnh của vật qua thấu kính.
b) Xác định kích thước và vị trí của ảnh.
Bài 4
Một thấu kính hội tụ có tiêu cự 6 cm. Vật sáng AB là một đoạn thẳng đặt vuông góc trục chính của thấu kính cho ảnh cách vật 25 cm. Xác định vị trí vật và ảnh.
Bài 5
Một điểm sáng S đặt trên trục chính của thấu kính hội tụ, tiêu cự f = 15 cm cho ảnh rõ nét trên màn M đặt vuông góc với trục chính của thấu kính. Di chuyển điểm sáng S về gần thấu kính đoạn 5 cm so với vị trí cũ thì màn phải dịch chuyển đi 22,5 cm mới lại thu được ảnh rõ nét.
a) Hỏi màn phải dịch chuyển ra xa hay lại gần thấu kính, vì sao?
b) Xác định vị trí điểm sáng S và màn lúc đầu.
Bài 6:
Cho một thấu kính có hai mặt lồi. Khi đặt trong không khí có độ tụ D 1 , khi đặt trong chất lỏng có chiết suất là n’= 1,68 thì thấu kính lại có độ tụ D 2 = – (D 1 /5). Hỏi chiết suất n của thấu kính là bao nhiêu?
Bài 7: Cho thủy tinh làm thấu kính có chiết suất n = 1,5.
TÍnh tiêu cự của các thấu kính khi đặt trong không khí. Nếu:
a) Hai mặt lồi có bán kính 10cm và 30cm
b) Mặt lồi có bán kính 10cm và mặt lõm có bán kính 30cm.
Bài 8: Một vật sáng AB có dạng mũi tên cao 6 cm đặt vuông góc trục chính của thấu kính hội tụ, cách thấu kính 15cm. Thấu kính có tiêu cự 10 cm.
a) Dựng ảnh của vật qua thấu kính.
b) Xác định kích thước và vị trí của ảnh.
Bài 9: Dùng thấu kính hội tụ có tiêu cự f = 4 cm, người ta thu được ảnh rõ nét của một vật sáng AB đặt trên trục chính và cách thấu kính đoạn 12 cm. Sau đó dịch chuyển vật sáng AB theo phương vuông góc với trục chính một đoạn 3 cm thì ảnh sẽ dịch chuyển như thế nào. Tính độ dịch chuyển của ảnh khi đó (so với trục chính).
Bài 10:
Thấu kính hội tụ có tiêu cự f có đường rìa hình tròn và màn đặt sau thấu kính cách thấu kính đoạn 60 cm, vuông góc với trục chính thấu kính. Di chuyển điểm sáng S trên trục chính thấu kính (bên kia màn so với thấu kính) ta lần lượt tìm được hai vị trí S lần lượt cho trên màn hai vòng tròn sáng có đường kính bằng đường kính rìa của thấu kính. Hai vị trí này cách nhau 8 cm.
a) Tìm tiêu cự thấu kính.
b) Từ vị trí điểm sáng gần thấu kính hơn, ta dịch điểm sáng đi 6 cm về phía gần thấu kính. So sánh đường kính vòng tròn sáng trên màn với đường kính rìa thấu kính.
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:












 Đề thi học kì 1 Lớp 11
Đề thi học kì 1 Lớp 11
 Đề thi học kì 2 Lớp 11
Đề thi học kì 2 Lớp 11
 Soạn văn 11 Kết nối tri thức
Soạn văn 11 Kết nối tri thức
 Soạn văn 11 Chân trời sáng tạo
Soạn văn 11 Chân trời sáng tạo
 Soạn văn 11 Cánh Diều
Soạn văn 11 Cánh Diều
 Toán 11 Kết nối tri thức
Toán 11 Kết nối tri thức
 Toán 11 Chân trời sáng tạo
Toán 11 Chân trời sáng tạo
 Toán 11 Cánh Diều
Toán 11 Cánh Diều
 Hóa 11 KNTT
Hóa 11 KNTT









