Vật lí 11 Bài 4: Bài tập về dao động điều hòa Giải Lý 11 Kết nối tri thức trang 17, 18, 19

Soạn Lí 11 Kết nối tri thức với cuộc sống giúp các bạn học sinh có thêm nhiều gợi ý tham khảo để trả lời câu hỏi mở đầu, nội dung bài học trong SGK Bài tập về dao động điều hòa của Chương 1: Dao động

Giải Lý 11 Kết nối tri thức trang 18 được biên soạn với các lời giải chi tiết, đầy đủ và chính xác bám sát chương trình sách giáo khoa. Giải Lý 11 bài 4 Bài tập về dao động điều hòa là tài liệu cực kì hữu ích hỗ trợ các em học sinh lớp 11 trong quá trình giải bài tập. Đồng thời phụ huynh có thể sử dụng để hướng dẫn con em học tập và đổi mới phương pháp giải phù hợp hơn.

Vật lí 11 Bài 4: Bài tập về dao động điều hòa

• Câu hỏi Khởi động trang 17 Vật lí 11 Bài 4
• Vật lí 11 Kết nối tri thức trang 18

Câu hỏi Khởi động trang 17 Vật lí 11 Bài 4

Khi biết phương trình hoặc đồ thị của vật dao động điều hòa, làm thế nào để xác định được vận tốc và gia tốc của vật?

Gợi ý đáp án

Khi biết phương trình của dao động điều hòa ta có thể sử dụng phương pháp đạo hàm để xác định được vận tốc, gia tốc của vật hoặc có thể xác định các đại lượng đặc trưng của dao động điều hòa và sử dụng các công thức đã biết để tính.

Vật lí 11 Kết nối tri thức trang 18

Bài 1 trang 18

Một vật dao động điều hòa có phương trình là x = 2cos(4πω − \(\frac{\pi }{6}\)) (cm). Hãy cho biết biên độ, tần số góc, chu kì, tần số, pha ban đầu và pha của dao động ở thời điểm t = 1s.

Gợi ý đáp án

Ta có:

• Biên độ A = 2 (cm)
• Tần số góc \(\omega = 4 \pi\) (rad/s)
• Chu kì T = \(\frac{2\pi}{\omega}\) = 0,5 (s)
• Tần số f = \(\frac{\omega}{2\pi}\) = 2 (Hz)
• Pha ban đầu \(\varphi = - \frac{\pi}{6}\) (rad)
• Pha của dao động ở thời điểm t = 1s là \(\varphi_{1} = - \frac{23\pi}{6}\) (rad)

Bài 2 trang 18

Một vật dao động điều hòa dọc theo trục Ox, quanh điểm gốc 0, với biên độ A = 10 cm và chu kì T = 2 s. Tại thời điểm t= 0,vật có li độ x = A.

a) Viết phương trình dao động của vật.

b) Xác định thời điểm đầu tiên vật qua vị trí có li độ x = 5 cm.

Gợi ý đáp án

a) Ta có: T = 2s \(\rightarrow \omega = \frac{2\pi}{T} = \pi\) (rad/s)

Tại thời điểm t = 0, vật có li độ x = \(A \rightarrow \varphi\) = 0 (rad)

Phương trình dao động là: x = \(10cos\pi t\) (cm)

b) Thời điểm đầu tiên vật qua vị trí có li độ x = 5 cm là \(\frac{1}{3}\) (s)

Bài 3 trang 19

Hình 4.2 là sơ đồ của một bàn xoay hình tròn, có gắn một thành nhỏ cách tâm bàn 15 cm. Bàn xoay được chiếu sáng bằng nguồn sáng rộng, song song, hướng chiếu sáng từ phía trước màn để bóng đổ lên màn hình. Một con lắc đơn dao động điều hòa phía sau bàn xoay với biên độ bằng khoảng cách từ thanh nhỏ đến tâm bàn xoay. Tốc độ quay của bàn quay được điều chỉnh là 2π rad/s. Bóng của thanh nhỏ và quả nặng của con lắc luôn trùng nhau.

a) Tại sao nói dao động của bóng của thanh nhỏ và quả nặng là đồng pha?

b) Viết phương trình dao động của con lắc. Chọn gốc thời gian là lúc con lắc ở vị trí hiển thị trong Hình 4.2

c) Bàn xoay đi một góc 60° tử vị trí ban đầu, tính li độ của con lắc và tốc độ của nó tại thời điểm này.

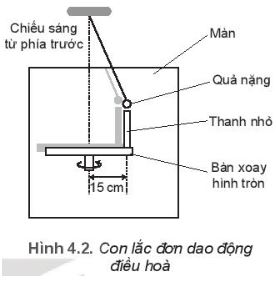
Gợi ý đáp án

a) dao động của bóng của thanh nhỏ và quả nặng đồng pha với nhau vì hai dao động có cùng tần số và pha dao động

b) Biên độ dao động của con lắc A = 15 (cm)

Tần số góc ω = \(2\pi\) (rad)

Từ hình vẽ và hướng di chuyển của con lắc ta có pha ban đầu φ = 0 (rad)

Phương trình dao động của con lắc là: x = 15cos\(2\pi\) (cm)

c) Bàn xoay đi một góc 60° từ vị trí ban đầu ta có pha dao động của con lắc là \(\frac{\pi }{3}\)

Li độ của con lắc là x = 7.5 cm

Vận tốc của con lắc là v = 81,62 cm/s

Bài 4 trang 19

Hình 4.3 là đồ thị li độ – thời gian của một vật dao động điều hòa.

a) Xác định biên độ, chu kì, tần số, tần số góc và pha ban đầu của vật dao động.

b) Viết phương trình dao động của vật.

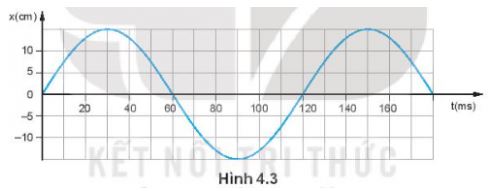
Gợi ý đáp án

a) Biên độ A = 15 (cm)

Chu kì T = 120 (ms) = 0,12 (s)

Tần số f = 25/3 (Hz)

Tần số góc \(\omega = \frac{2\pi}{T}=\frac{2\pi}{0,12}=\frac{50\pi}{3}\) (rad/s)

Pha ban đầu \(\varphi = -\frac{\pi}{2}\)

b) Phương trình dao động của vật là: \(x=15cos(\frac{50\pi}{3}t -\frac{\pi}{2} )\) (cm)

Bài 5 trang 19

Đồ thị li độ – thời gian của hai vật dao động điều hòa A và B có cùng tần số nhưng lệch pha nhau (Hình 4.4).

a) Xác định li độ dao động của vật B khi vật A có li độ cực đại và ngược lại.

b) Hãy cho biết vật A hay vật B đạt tới li độ cực đại trước.

c) Xác định độ lệch pha giữa dao động của vật A so với dao động của vật B.

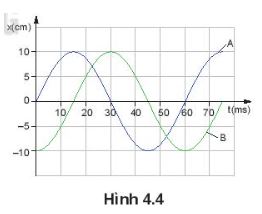
Gợi ý đáp án

a) Khi vật A có li độ cực đại thì vật B ở vị trí cân bằng và ngược lại khi vật B có li độ cực đại thì vật A ở vị trí cân bằng

b) Vật A đạt li độ cực đại trước vật B

c) Độ lệch pha giữa dao động của vật A so với dao dộng của vật B là: Δω = π dao động A sớm pha hơn dao động B