Vật lí 11 Bài 17: Khái niệm điện trường Giải Lý 11 Kết nối tri thức trang 65, 66, 67, 68, 69

Bài trước

Mục lục

Bài sau

Giải Vật lý 11 trang 65, 66, 67, 68, 69 Kết nối tri thức với cuộc sống giúp các em học sinh lớp 11 có thêm nhiều gợi ý tham khảo để biết cách trả lời các câu hỏi bài học bài 16: Khái niệm điện trường thuộc Chương 3: Điện trường.

Giải Lý 11 Kết nối tri thức bài 16 các em sẽ hiểu được kiến thức về điện trường, cường độ dòng điện và nhanh chóng trả lời toàn bộ các câu hỏi trang 65, 66, 67, 68, 69 trong sách giáo khoa Vật lí 11. Đồng thời qua đó giúp quý thầy cô tham khảo để soạn giáo án cho học sinh của mình thuận tiện hơn.

Vật lí 11 Bài 17: Khái niệm điện trường

I. Khái niệm điện trường

Hoạt động

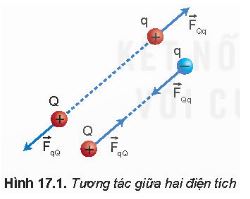
Đặt điện tích q cách điện tích Q một khoảng r (Hình 17.1)

Có phải không khí đã truyền tương tác điện từ điện tích Q tới điện tích q hay không?
Vùng không gian bao quanh một nam châm có từ trường. Tương tự như vậy, vùng không gian bao quanh một điện tích có điện trường. Ta có thể phát hiện sự tồn tại của điện trưởng bằng cách nào?

Gợi ý đáp án

1. Không phải không khí đã truyền tương tác điện từ điện tích Q đến điện tích q mà do điện trường xung quanh điện tích đã truyền tương tác điện và khi đặt trong chân không vẫn xảy ra tương tác này.

2. Để nhận biết được điện trường đang tồn tại không thể nhận biết bằng mắt thường, cần phải thông qua những hiện tượng vật lí mới có thể quan sát được có điện trường hay không. Có thể đặt một điện tích điểm vào trong đó, nếu có lực tác dụng lên điện tích thì tồn tại điện trường, nếu không có lực tác dụng lên điện tích thì không tồn tại điện trường.

II. Cường độ điện trường

Hoạt động 1:

Hãy chứng tỏ rằng vectơ cường độ điện trường $\vec{E}$ $\vec{E}$ có:

+ Phương trùng với phương của lực điện tác dụng lên điện tích.

+ Chiều cùng với chiều của lực điện khi q > 0 ngược chiều với chiều của lực điện khi q < 0

+ Độ lớn của vectơ cường độ điện trưởng $\vec{E}$ $\vec{E}$ bằng độ lớn của lực điện tác dụng lên điện tích 1C đặt tại điểm ta xét.

Gợi ý đáp án

Ta có: $\vec{E}=\frac{\vec{F}}{q}$ $\vec{E}=\frac{\vec{F}}{q}$

Từ công thức ta thấy vectơ cường độ điện trường $\vec{E}$ $\vec{E}$ có phương trùng với phương của vectơ $\vec{F}$ $\vec{F}$ lực điện tác dụng lên điện tích

Với q > 0 thì $\vec{E}, \vec{F}$ $\vec{E}, \vec{F}$ cùng chiều với nhau

Với q < 0 thì $\vec{E}, \vec{F}$ $\vec{E}, \vec{F}$ ngược chiều với nhau

Nếu q = 1 thì E = F

Hoạt động 2: Xét điện trường của điện tích $Q= 6.10^{-14} C$ $Q= 6.10^{-14} C$ sử dụng đoạn thẳng dài 1 cm để biểu diễn cho độ lớn vectơ cường độ điện $E=\frac{10^{-10}}{6\pi \varepsilon _{0}}$ $E=\frac{10^{-10}}{6\pi \varepsilon _{0}}$ (V / m). Hãy tính và vẽ vectơ cường độ điện trường tại một điểm cách Q một khoảng 2 cm và 3 cm.

Gợi ý đáp án

Ta có: $E=\frac{\left | Q \right |}{4\pi\varepsilon _{0}r^{2}}=\frac{10^{-10}}{6\pi \varepsilon _{0}}\Leftrightarrow r = 0,03 (cm)$ $E=\frac{\left | Q \right |}{4\pi\varepsilon _{0}r^{2}}=\frac{10^{-10}}{6\pi \varepsilon _{0}}\Leftrightarrow r = 0,03 (cm)$

Vectơ cường độ điện trường tại một điểm cách Q một khoảng 3 cm có độ lớn $Q= 6.10^{-14} C$ $Q= 6.10^{-14} C$.

Cường độ điện trường tại một điểm cách Q 2cm có độ lớn là $E_{1}=\frac{\left | Q \right |}{4\pi\varepsilon _{0}r_{1}^{2}}= \frac{15.10^{-11}}{4\pi \varepsilon _{0}} (V/m)$ $E_{1}=\frac{\left | Q \right |}{4\pi\varepsilon _{0}r_{1}^{2}}= \frac{15.10^{-11}}{4\pi \varepsilon _{0}} (V/m)$

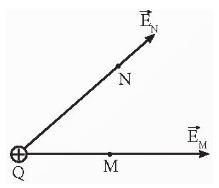
Điểm M biểu diễn cường độ điện trường tại điểm cách Q 2cm

Điểm N biểu diễn cường độ điện trường tại điểm cách Q 3cm

Câu hỏi 1: Hãy chứng tỏ rằng: Độ lớn cường độ điện trường tại một điểm trong công thức (17.1) bằng độ lớn của lực điện tác dụng lên một đơn vị điện tích đặt tại điểm đó.

Gợi ý đáp án

Ta có: E = $\frac{F}{q}$ $\frac{F}{q}$với q = 1 C thì E = F

Câu hỏi 1:

Một điện tích điểm Q = 6.10⁻¹³ C đặt trong chân không.

a) Xác định phương, chiều, độ lớn của cường độ điện trường do điện tích điểm Q gây ra tại một điểm cách nó một khoảng 1 cm, 2 cm, 3 cm.

b) Nhận xét về cường độ điện trường ở những điểm gần điện tích Q và ở những điểm cách xa điện tích Q.

c) Từ các nhận xét trên, em hãy mô tả cường độ điện trường do một điện tích điểm dương Q đặt trong chân không gây ra tại một điểm cách nó một khoảng r. Vẽ hình minh hoạ.

Gợi ý đáp án

a) Độ lớn của cường độ điện trường do điện tích điểm Q gây ra tại một điểm cách nó một khoảng 1 cm là

$F=\frac{\left | Q \right |}{4\pi\varepsilon _{0}r^{2}}=\frac{3.10^{-9}}{2\pi \varepsilon _{0}} (V/m)$ $F=\frac{\left | Q \right |}{4\pi\varepsilon _{0}r^{2}}=\frac{3.10^{-9}}{2\pi \varepsilon _{0}} (V/m)$

Độ lớn của cường độ điện trường do điện tích điểm Q gây ra tại một điểm cách nó một khoảng 2 cm là

$F=\frac{\left | Q \right |}{4\pi\varepsilon _{0}r^{2}}=\frac{15.10^{-10}}{4\pi \varepsilon _{0}} (V/m)$ $F=\frac{\left | Q \right |}{4\pi\varepsilon _{0}r^{2}}=\frac{15.10^{-10}}{4\pi \varepsilon _{0}} (V/m)$

Độ lớn của cường độ điện trường do điện tích điểm Q gây ra tại một điểm cách nó một khoảng 3 cm là

$F=\frac{\left | Q \right |}{4\pi\varepsilon _{0}r^{2}}=\frac{5.10^{-10}}{3\pi \varepsilon _{0}} (V/m)$ $F=\frac{\left | Q \right |}{4\pi\varepsilon _{0}r^{2}}=\frac{5.10^{-10}}{3\pi \varepsilon _{0}} (V/m)$

b) Cường độ điện trường của những điểm gần Q lớn hơn những điểm xa Q

c) Cường độ điện trường do một điện tích điểm Q đặt trong chân không gây ra tại một điểm M cách nó một khoảng r có phương QM, có chiếu từ Q đến M nếu Q > 0 và có chiều từ M đến Q nếu Q < 0. Độ lớn của cường độ điện trường tại M có giá trị bằng $E=\frac{10^{-10}}{6\pi \varepsilon _{0}}$ $E=\frac{10^{-10}}{6\pi \varepsilon _{0}}$. Ta có thể thấy những điểm có cùng khoảng cách đến Q cường độ điện trường sẽ có độ lớn bằng nhau, những điểm ở gần Q hơn sẽ có độ lớn cường độ điện trường lớn hơn và ngược lại.

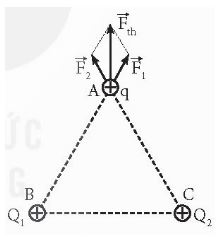
Hoạt động 3: Nếu trong không gian có hai điện tích điểm dương Q₁ = Q₂ được đặt ở hai điểm B và C, một điện tích thử q được đặt tại một điểm A như Hình 17.4. Hãy mô tả bằng hình vẽ lực điện tổng hợp do Q₁ và Q₂ tác dụng lên điện tích thử q.

Gợi ý đáp án

Sử dụng quy tắc hình bình hành để tổng hợp lực tác dụng lên điện tích q tại A theo quy tắc $\vec{F}_{1}+\vec{F}_{2}=\vec{F}$ $\vec{F}_{1}+\vec{F}_{2}=\vec{F}$

Câu hỏi 2: Đặt điện tích điểm $Q_{1} = 6.10 ^ {- 8} C$ $Q_{1} = 6.10 ^ {- 8} C$ tại điểm A và điện tích điểm $Q_{2} = - 2.10 ^ {- 8 } C$ $Q_{2} = - 2.10 ^ {- 8 } C$ tại điểm B cách A một khoảng bằng 3 cm (Hình 17.5). Hãy xác định những điểm mà cường độ điện trường tại đó bằng 0.

Gợi ý đáp án

Cường độ điện trường bằng 0 khi:

$\vec{E}_{1}+\vec{E}_{2}=\vec{E}=\vec{0}\Rightarrow \vec{E}_{1}=-\vec{E}_{2}$ $\vec{E}_{1}+\vec{E}_{2}=\vec{E}=\vec{0}\Rightarrow \vec{E}_{1}=-\vec{E}_{2}$

$\Rightarrow \left\{\begin{matrix}E_{1}\uparrow\downarrow E_{2}\\E_{1} =E_{2}\end{matrix}\right.$ $\Rightarrow \left\{\begin{matrix}E_{1}\uparrow\downarrow E_{2}\\E_{1} =E_{2}\end{matrix}\right.$

Vì $\left|q_{1}\right|>\left|q_{2}\right| \Rightarrow$ $\left|q_{1}\right|>\left|q_{2}\right| \Rightarrow$ Điểm đó thuộc đường thẳng AB và ngoài đoạn AB, gần B hơn (r₁ > r₂)

$\Rightarrow\left\{\begin{matrix}r_{1}-r_{2}=AB\\ \frac{r_{1}^{2}}{r_{2}^{2}}=\frac{\left|q_{1}\right|}{\left|q_{2}\right|}\end{matrix}\right. \Rightarrow r1=0,071m;r2=0,041m$ $\Rightarrow\left\{\begin{matrix}r_{1}-r_{2}=AB\\ \frac{r_{1}^{2}}{r_{2}^{2}}=\frac{\left|q_{1}\right|}{\left|q_{2}\right|}\end{matrix}\right. \Rightarrow r1=0,071m;r2=0,041m$

Vậy điểm cần tìm cách A 7,1 cm và cách B 4,1 cm

Câu hỏi 3:

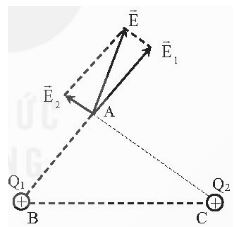
Cho tam giác ABC vuông tại A có AB = 3 cm và AC = 4 cm. Tại điểm B ta đặt điện tích $Q_{1} = 4,5.10 ^ {- 8} C$ $Q_{1} = 4,5.10 ^ {- 8} C$ tại điểm C ta đặt điện tích $Q_{2} = 2,1 ^{ - 8} C$ $Q_{2} = 2,1 ^{ - 8} C$

a) Tính độ lớn của cường độ điện trường do mỗi điện tích trên gây ra tại A.

b) Tính cường độ điện trường tổng hợp tại A.

Gợi ý đáp án

a) Cường độ điện trường do điện tích Q1 gây ra tại A là:

$E_{1}=\frac{\left|Q_{1}\right |}{4\pi \varepsilon _{0}AB^{2}}=\frac{5.10^{-5}}{4\pi \varepsilon _{0}} (V/m)$ $E_{1}=\frac{\left|Q_{1}\right |}{4\pi \varepsilon _{0}AB^{2}}=\frac{5.10^{-5}}{4\pi \varepsilon _{0}} (V/m)$

Cường độ điện trường do điện tích Q2 gây ra tại A là:

$E_{2}=\frac{\left |Q_{2} \right |}{4\pi \varepsilon _{0}AC^{2}}=\frac{25.10^{-6}}{8\pi \varepsilon _{0}} (V/m)$ $E_{2}=\frac{\left |Q_{2} \right |}{4\pi \varepsilon _{0}AC^{2}}=\frac{25.10^{-6}}{8\pi \varepsilon _{0}} (V/m)$

b) Ta có : $\vec{E_{1}}\perp\vec{E_{2}} \Rightarrow E=\sqrt{E_{1}^{2}+E_{2}^{2}} = 463427 (V/m)$ $\vec{E_{1}}\perp\vec{E_{2}} \Rightarrow E=\sqrt{E_{1}^{2}+E_{2}^{2}} = 463427 (V/m)$

Câu hỏi 4: Một hạt bụi mịn loại pm2.5 có điện tích bằng 1,6.10⁻¹⁹ C lơ lửng trong không khí ở nơi có điện trường của Trái Đất bằng 120 V/m. Bỏ qua trọng lực, tính lực điện của Trái Đất tác dụng lên hạt bụi mịn và từ đó giải thích lí do hạt bụi loại này thường lơ lửng trong không khí.

Gợi ý đáp án

Ta có: Lực điện tác dụng vào hạt bụi trong điện trường là: F = E.q = 120.1,6.10⁻¹⁹ = 1,92.10⁻¹⁷

Vì hạt bụi mịn có điện tích dương nên lực điện sé có chiều theo chiều điện trường, tức là hướng từ trên xuống dưới mặt đất. Lực điện này là một trong những nguyên nhân làm cho các hạt bụi mịn không bị gió cuỗn bay lên cao được.

Chia sẻ bởi: