| |
Tuyển tập 217 bài toán đồ thị và bảng biến thiên Bài toán đồ thị và bảng biến thiên có đáp án
Tuyển tập 217 bài toán đồ thị và bảng biến thiên là tài liệu cực kì hữu ích mà Eballsviet.com muốn giới thiệu đến các bạn học sinh lớp 12 cùng tham khảo.
Tài liệu bao gồm 93 trang tuyển tập 217 câu hỏi và bài toán đồ thị và bảng biến thiên thuộc chương trình Giải tích 12 chương 1 có đáp án và lời giải chi tiết. Các bài toán với đầy đủ 4 mức độ nhận thức, từ dễ đến khó, phù hợp với nhiều đối tượng học sinh: yếu – trung bình – khá – giỏi. Tài liệu nhằm giúp học sinh khối 12 tổng ôn tập chủ đề ứng dụng đạo hàm để khảo sát sự biến thiên và vẽ đồ thị hàm số, hướng đến kỳ thi THPT Quốc gia môn Toán. Mời các bạn cùng tham khảo và tải tài liệu tại đây.
Tuyển tập 217 bài toán đồ thị và bảng biến thiên

L
A
T
E
X PAGE TOÁN HỌC SƠ CẤP https://www.facebook.com/MATHDDT/
Tuyển tập 217 câu đồ thị, bảng biến thiên
mức độ Y-B-K-G
Câu 1. Cho hàm số f (x) xác định trên R \
{
1
}
, liên tục trên mỗi khoảng xác định và có bảng biến
thiên như hình dưới đây.
x
y
0
y
−∞
−1
1
3
+∞
+
0
− −
0
+
−∞−∞
−2−2
−∞
+∞
22
+∞+∞
A Hàm số nghịch biến trên khoảng (−1; 3).
B Hàm số đồng biến trên các khoảng (−∞; −2) và (2; +∞).
C Hàm số đồng biến trên các khoảng (−∞; −1) và (3; +∞).
D Hàm số nghịch biến trên khoảng (−∞; 1).
Hướng dẫn giải
1. Sai vì khoảng (−1; 3) không nằm trong tập xác định.
2. Sai vì trong khoảng (2; +∞) thì khoảng (2; 3) hàm nghịch biến.
3. Đúng.
4. Sai vì trong khoảng (−1; 0) hàm nghịch biến.
Chọn đáp án C
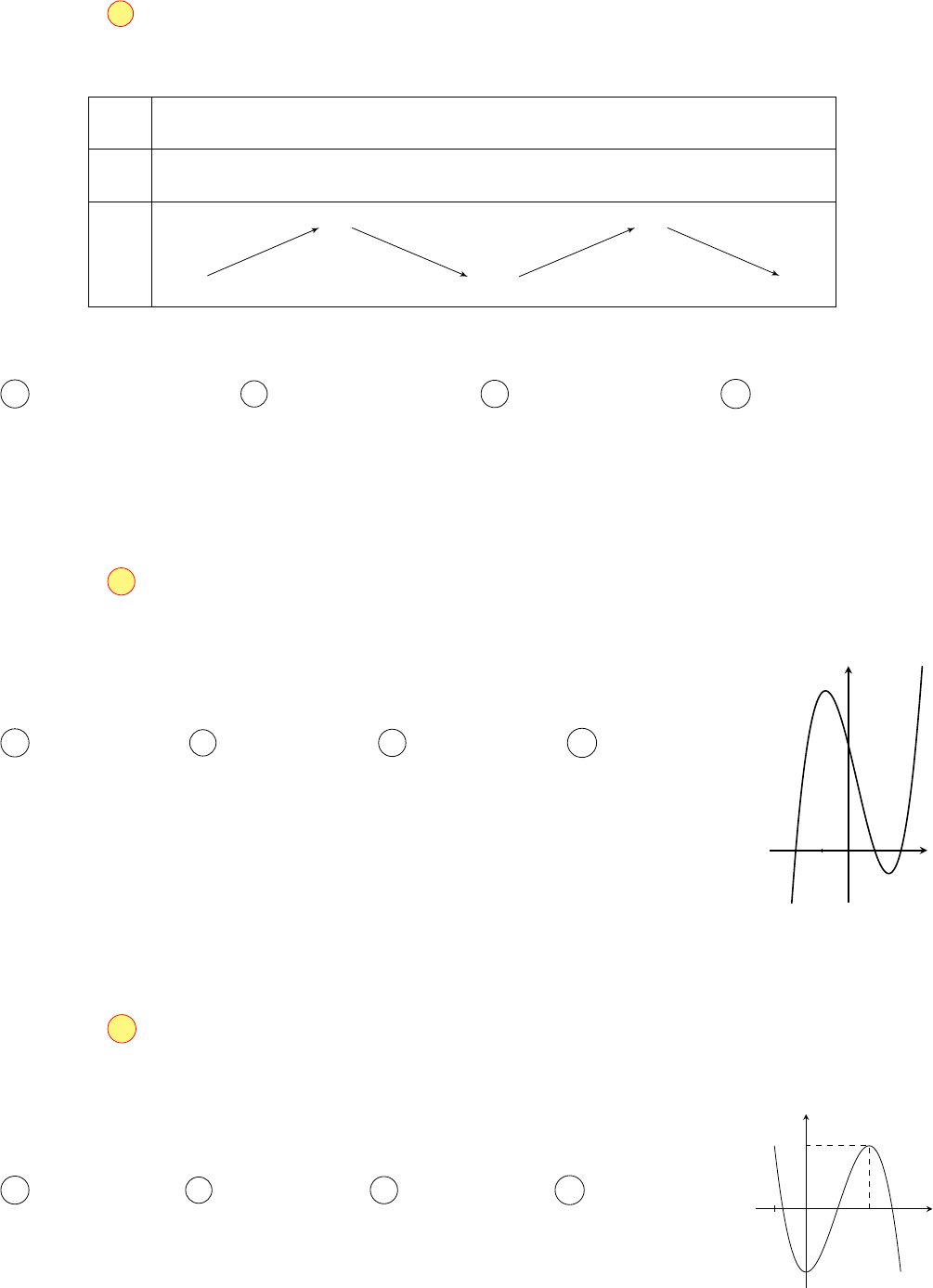
Câu 2.
Cho hàm số y = f (x). Hàm số y = f
0
(x) có đồ thị như hình vẽ. Hàm
số y = f (2 + e
x
) nghịch biến trên khoảng
A (0; +∞). B (−∞ ; 0). C (−1; 3). D (−2; 1).
O
x
y
3
−1
−4
2
Hướng dẫn giải
y
0
= f
0
(2 + e
x
) = e
x
. f
0
(t) với t = 2 + e
x
.
Do e
x
> 0 ∀x nên y
0
và f
0
(t) cùng dấu. Vậy để y nghịch biến thì f (t) nghịch biến trên khoảng
tương ứng.
"Toán học là môn thể dục của trí tuệ "–Isocrates Trang 1
L
A
T
E
X PAGE TOÁN HỌC SƠ CẤP https://www.facebook.com/MATHDDT/
Nhìn vào đồ thị ta thấy f
0
(t) ≤ 0 ∀t ≥ 3.
Do 2 + e
x
≤ 3 ⇔ x ≤ 0 nên hàm số y = f (2 + e
x
) nghịch biến trên (−∞; 0).
Chọn đáp án B
Câu 3. Cho hàm số y = f (x) có bảng biến thiên như sau
x
y
0
y
−∞
−2
0
2
+∞
+
0
−
0
+
0
−
−∞−∞
33
−1−1
33
−∞−∞
Hàm số y = f (x) + 2018 đồng biến trên khoảng nào dưới đây?
A (−2; 0). B (3; +∞). C (0; 2). D (2018; 2020).
Hướng dẫn giải
Đồ thị hàm số y = f (x) + 2018 có được bằng cách tịnh tiến đồ thị hàm số y = f (x) lên trên 2018 đơn
vị nên không làm thay đổi các khoảng đồng biến.
Vậy hàm số y = f (x) + 2018 đồng biến trên các khoảng (−∞; −2) và (0; 2).
Chọn đáp án C
Câu 4.
Cho hàm số y = f (x) xác định và liên tục trên R, có đồ thị ở hình bên. Hàm số
y = f (x) nghịch biến trên khoảng nào dưới đây?
A (0; 1). B (−∞ ; 0). C (1; 2). D (2; +∞).
x
y
−2
−1 1
2
O
Hướng dẫn giải
Nhìn đồ t hị ta thấy hàm số đi xuống trên khoảng (−1; 1) do đó hàm số nghịch biến trên khoảng
(0; 1).
Chọn đáp án A
Câu 5.
Cho hàm số y = f (x) có đồ thị như hình vẽ. Hàm số y = f (x) đồng biến trên
khoảng nào dưới đây?
A (0; 2). B (−2; 2). C (2; +∞). D (−∞ ; 0).
O
x
y
−1
1
2
−2
2
Hướng dẫn giải
"Toán học là môn thể dục của trí tuệ "–Isocrates Trang 2

L
A
T
E
X PAGE TOÁN HỌC SƠ CẤP https://www.facebook.com/MATHDDT/
Dựa vào đồ thị ta thấy hàm số đồng biến trên khoảng (0; 2), nghịch biến trên các khoảng (−∞; 0) và
(2; +∞).
Chọn đáp án A
Câu 6. Cho hàm số y = f (x) có bảng biến thiên như sau:
x
f
0
(x)
f (x)
−∞
−2
0
2
+∞
+
0
− −
0
+
−∞−∞
−2−2
+∞
+∞
66
+∞+∞
Mệnh đề nào dưới đây là đúng?
A Hàm số nghịch biến trên khoảng (0; 2). B Hàm số nghịch biến trên khoảng (−2; 2).
C Hàm số nghịch biến trên khoảng (−∞; −2). D Hàm số đồng biến trên khoảng (−∞; 0).
Hướng dẫn giải
Theo bảng biến thiên, hàm số đồng biến trên khoảng (0; 2).
Chọn đáp án A
Câu 7.
Cho hàm số y = f (x) có đồ thị như hình vẽ bên. Hàm số y = f (x)
đồng biến trên khoảng
A (−1; +∞). B (−1; 1). C (−∞ ; 1). D (−∞ ; −1).
O
x
y
−2
−2
−1
−1
1
1
2
2
3
3
Hướng dẫn giải
Trên khoảng (−∞; −1) đồ thị hàm số "đi lên" từ trái sang phải nên hàm số đồng biến trên (−∞; −1).
Chọn đáp án D
Câu 8. Cho hàm số y = f (x) có bảng biến thiên như sau:
x
y
0
y
−∞
0
2
+∞
+
0
−
0
+
−∞−∞
44
00
+∞+∞
Trong các mệnh đề sau, mệnh đề nào đúng?
"Toán học là môn thể dục của trí tuệ "–Isocrates Trang 3
Liên kết tải về
Tuyển tập 217 bài toán đồ thị và bảng biến thiên
982,5 KB
Tải về
Có thể bạn quan tâm
-

Vẽ kỹ thuật với AutoCad - Sách hướng dẫn sử dụng AutoCad
-

Bộ đề đọc hiểu Ngữ văn lớp 7 (Chương trình mới)
-

Văn mẫu lớp 7: Biểu cảm về loài cây em yêu
-

Dàn ý viết bài văn kể lại một chuyến đi đáng nhớ của em
-

Hoạt động trải nghiệm 6: Phòng tránh thiên tai và giảm thiểu biến đổi khí hậu
-

Kể về một anh hùng chống ngoại xâm mà em biết (60 mẫu)
-
Truyện cổ tích Việt Nam - Tổng hợp truyện cổ tích cho bé
-

Toán lớp 5 Bài 19: Hàng của số thập phân. Đọc, viết số thập phân
-

Kể về một người mà em quý mến nhất (ông bà, cha mẹ, hàng xóm…)
-

Giấy xác nhận sinh hoạt hè - Mẫu giấy xác nhận sinh hoạt hè tại địa phương
Xác thực tài khoản!
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:
Số điện thoại chưa đúng định dạng!
Sắp xếp theo
Đóng
Chỉ thành viên Download Pro tải được nội dung này!
Download Pro - Tải nhanh, website không quảng cáo!
Tìm hiểu thêm












