Tổng hợp lý thuyết và công thức tính nhanh Hình học 12 Công thức Hình học 12

Công thức tính nhanh Hình học 12 và lý thuyết gồm 50 trang tổng hợp toàn bộ kiến thức lý thuyết và các công thức Hình học có trong chương trình Toán 12.

Công thức tính nhanh Hình học 12 được trình bày rất khoa học từ lý thuyết, công thức ví dụ minh họa và các dạng bài tập rất logic giúp người học dễ hình dung và hiểu rõ kiến thức. Thông qua tài liệu này các bạn lớp 12 nhanh chóng nắm vững kiến thức để giải nhanh các bài tập hình không gian. Bên cạnh đó các bạn xem thêm bộ đề ôn thi THPT Quốc gia môn Toán, phân dạng câu hỏi và bài tập trong đề thi THPT Quốc gia môn Toán.

1. Khối lăng trụ và khối chóp

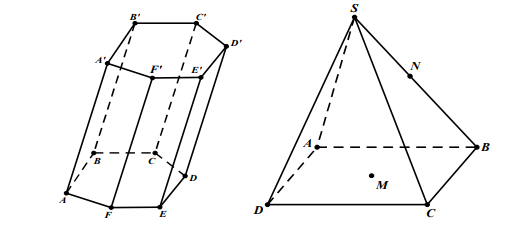
Khối lăng trụ (chóp) là phần không gian được giới hạn bởi một hình lăng trụ (chóp) kể cả hình lăng trụ (chóp) ấy.

Khối chóp cụt là phần không gian được giới hạn bởi một hình chóp cụt kể cả hình chóp cụt ấy.

Điểm không thuộc khối lăng trụ (khối chóp, khối chóp cụt) được gọi là điểm ngoài của khối lăng trụ (khối chóp, khối chóp cụt).

Điểm thuộc khối lăng trụ nhưng không thuộc hình lăng trụ ứng với khối lăng trụ (khối chóp, khối chóp cụt) đó được gọi là điểm trong của khối lăng trụ (khối chóp, khối chóp cụt).

2. Khái niệm về hình đa diện và khối đa diện

2.1. Khái niệm về hình đa diện

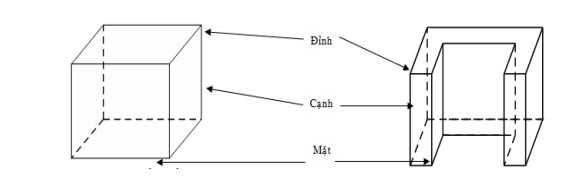
Hình đa diện (gọi tắt là đa diện) là hình được tạo bởi một số hữu hạn các đa giác thỏa mãn hai tính chất: Hai đa giác phân biệt chỉ có thể hoặc không có điểm chung, hoặc chỉ có một đỉnh chung, hoặc chỉ có một cạnh chung. Mỗi cạnh của đa giác nào cũng là cạnh chung của đúng hai đa giác. Mỗi đa giác gọi là một mặt của hình đa diện. Các đỉnh, cạnh của các đa giác ấy theo thứ tự được gọi là các đỉnh, cạnh của hình đa diện.

2.2. Khái niệm về khối đa diện

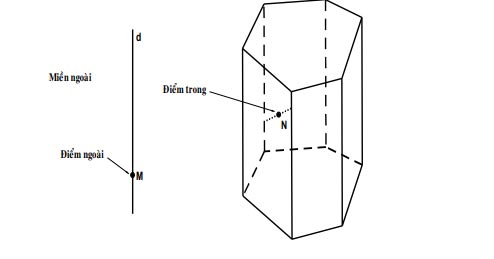
Khối đa diện là phần không gian được giới hạn bởi một hình đa diện, kể cả hình đa diện đó.

Những điểm không thuộc khối đa diện được gọi là điểm ngoài của khối đa diện.

Những điểm thuộc khối đa diện nhưng không thuộc hình đa diện đó được gọi là điểm trong của khối đa diện. Tập hợp các điểm trong được gọi là miền trong, tập hợp những điểm ngoài được gọi là miền ngoài của khối đa diện.

Mỗi hình đa diện chia các điểm còn lại của không gian thành hai miền không giao nhau là miền trong và miền ngoài của hình đa diện, trong đó chỉ có miền ngoài là chứa hoàn toàn một đường thẳng nào đó.

3. Công thức hình phẳng

3.1. Hệ thức lượng trong tam giác

3.1.1. Cho \(\triangle A B C\) vuông tại A, đường cao A H

\(- A B^2+A C^2=B C^2\)

\(- A B^2=B H B C\)

\(- A C^2=C H-B C\)

\(- A C^2=C H-B C\)

\(- A H^2= BH.HC\)

\(- \frac{1}{A H^2}=\frac{1}{A B^2}+\frac{1}{A C^2}\)

\(- A B=B C \cdot \sin C=B C \cdot \cos B=A C \cdot \tan C=A C \cdot \cot B\)

3.1.2. Cho \(\triangle A B C\)có độ dài ba cạnh là: a, b, c độ dại cạc trung tuyến là \(m_a, m_b, m_c\) bán kính đường tròn ngoại tiếp R; bán kính đường tròn nội tiếp r nửa chu vi p.

- Định lý hàm số cosin:

\(a^2=b^2+c^2-2 k c \cdot \cos A ; b^2=c^2+a^2-2 c a \cdot \cos B ; c^2=a^2+b^2-2 a b \cdot \cos C\)

- Định lý hàm số sin:

\(\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2 R\)

- Độ dài trung tuyến:

\(m^2=\frac{b^2+c^2}{2}-\frac{a^2}{4} ; m^2=\frac{c^2+a^2}{2}-\frac{b^2}{4} ; m^2=\frac{a^2+b^2}{2}-\frac{c^2}{4}\)

3.2. Các công thức tính diện tích

3. 2.1. Tam giác

\(- S=\frac{1}{2} a \cdot h_\alpha=\frac{1}{2} b h_k=\frac{1}{2} c h\)

\(- S=\frac{1}{2} b c \cdot \sin A=\frac{1}{2} c a \sin B=\frac{1}{2} a b \sin C\)

\(- S=\frac{a b c}{4 R}\)

- S=p r

\(- S=\sqrt{p(p-a)(p-b)(p-c)}\)

\(- \triangle A B C\) vuông tại A: \(S=\frac{A B \cdot A C}{2}=\frac{B C \cdot A H}{2}\)

\(- \triangle A B C\) đều, cạnh a: \(A H=\frac{a \sqrt{3}}{2}, S=\frac{a^2 \sqrt{3}}{4}\)

3.2.2. Hình vuông

-\(S=a^2\) ( a : cạnh hình vuông)