Tài liệu tự học chủ đề đạo hàm Tài liệu ôn tập môn Toán lớp 11
Eballsviet.com xin giới thiệu đến các em học sinh lớp 11 Tài liệu tự học chủ đề đạo hàm được chúng tôi đăng tải ngay sau đây.
Đây là tài liệu vô cùng hữu ích, trình bày các lý thuyết cơ bản, các dạng toán thường gặp, bài tập cơ bản và nâng cao về chủ đề đạo hàm và các vấn đề có liên quan trong chương trình Đại số và Giải tích 11 chương 5. Sau đây là nội dung chi tiết, mời bạn đọc cùng tham khảo và tải tài liệu tại đây.
Tài liệu tự học chủ đề đạo hàm
GV. TRẦN QUỐC NGHĨA (Sưu tầm và biên tập) 1
ĐẠO HÀM
Vấn đề 1. ĐẠO HÀM VÀ Ý NGHĨA CỦA ĐẠO HÀM
Mở đầu
Nhiều bài toán của toán học, vật lí, hóa học, sinh học, kĩ thuật, … đòi hỏi phải tìm giới hạn
dạng:
0
0
0
lim
x x
f x f x
x x
trong đó
f x
là một hàm số đã cho của đối số
x
.
Qua Đại số và Giải tích 11, ta biết định nghĩa và kí hiệu của số gia đối số và số gia tương ứng
của hàm số:
Số gia đối số là
0
–
x x x
Số gia tương ứng của hàm số là
0
–
y f x f x
Ta sẽ dùng khái niệm và kí hiệu đó viết các giới hạn trên:
0
0
0
0
lim lim
x x x
f x f x
y
x x x
Định nghĩa đạo hàm
Cho hàm số
y f x
, xác định trên
;
a b
và
0
;
x a b
Giới hạn, nếu có, của tỉ số giữa số gia của hàm số và số gia của đối số tại
0
x
, khi số gia đối số
dần tới
0
, được gọi là đạo hàm của hàm số
y f x
tại điểm
0
x
.
Đạo hàm của hàm số
y f x
tại
0
x
được kí hiệu là
0
y x
hoặc
0
f x
:
0
0
0
0
lim
x x
f x f x
f x
x x
hoặc
0
0
lim
x
y
y x
x
Đạo hàm một bên
a. Đạo hàm bên trái của hàm số
y f x
tại điểm
0
x
, kí hiệu là
0
f x
được định nghĩa là
0
0
0
0
0
lim lim
x x x
f x f x
y
f x
x x x
trong đó
0
x x
được hiểu là
0
x x
và
0
x x
.
b. Đạo hàm bên phải của hàm số
y f x
tại điểm
0
x
, kí hiệu là
0
f x
được định nghĩa là
0
0
0
0
0
lim lim
x x x
f x f x
y
f x
x x x
trong đó
0
x x
được hiểu là
0
x x
và
0
x x
.
Định lí: Hàm số
y f x
có đạo hàm tại điểm
0
x
thuộc tập xác định của nó, nếu và chỉ nếu
0
f x
và
0
f x
tồn tại và bằng nhau. Khi đó ta có:
0 0 0
f x f x f x
.
Đạo hàm trên một khoảng
Định nghĩa:
a. Hàm số
y f x
được gọi là có đạo hàm trên khoảng
;
a b
nếu nó có đạo hàm tại mọi
điểm trên khoảng đó.
2
Chủ đề
TÀI LIỆU HỌC TẬP TOÁN 11 – HK2 – ĐẠO HÀM 2
b. Hàm số
y f x
được gọi là có đạo hàm trên đoạn
;
a b
nếu nó có đạo hàm trên khoảng
;
a b
và có đạo hàm bên phải tại
a
, đạo hàm bên trái tại
b
.
Qui ước: Từ nay, khi ta nói hàm số
y f x
có đạo hàm, mà không nói rõ trên khoảng nào,
thì điều đó có nghĩa là đạo hàm tồn tại với mọi giá trị thuộc tập xác định của hàm số đã cho.
Quan hệ giữa sự tồn tại của đạo hàm và tính liên tục của h.số
Định lí: Nếu hàm số
y f x
có đạo hàm tại điểm
0
x
thì nó liên tục tại điểm đó.
Chú ý: 1. Đảo lại không đúng, tức là một hàm số liên tục tại điểm
0
x
có thể không có
đạo hàm tại điểm đó
2. Như vậy, hàm số không liên tục tại x
0
thì không có đạo hàm tại điểm đó.
Ý nghĩa của đạo hàm
1. Ý nghĩa hình học
a. Tiếp tuyến của đường cong phẳng:
Cho đường cong phẳng
C
và một điểm cố định
0
M
trên
C
, M là điểm di động trên
C
. Khi đó
0
M M
là một cát
tuyến của
C
.
Định nghĩa: Nếu cát tuyến
0
M M
có vị trí giới hạn
0
M
T
khi điểm
M
di chuyể
n trên
C
và dần tới điểm
0
M
thì đường thẳng
0
M
T
được gọi là tiếp tuyến của đườ
ng cong
C
tại điểm
0
M
. Điểm
0
M
được gọi là tiếp điểm.
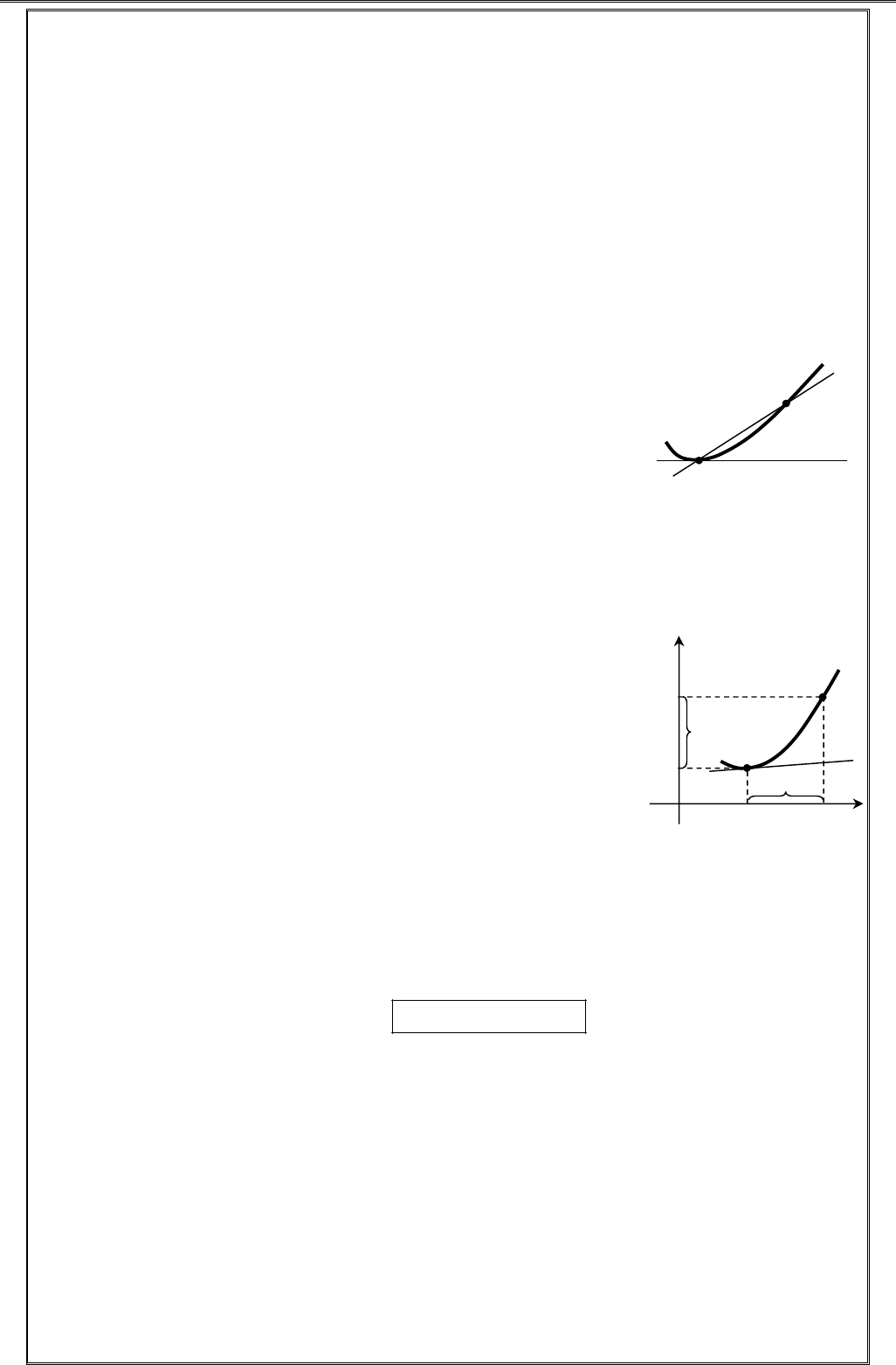
b. Ý nghĩa hình học của đạo hàm:
Cho hàm số
y f x
xác định trên khoảng
;
a b
và
có đạo hàm tại
0
;
x a b
, gọi
C
là đồ thị hàm số đó.
Định lí 1: Đạo hàm của hàm số
f x
tại điểm
0
x
là
hệ số góc của tiếp tuyến
0
M
T
của
C
tại điểm
0 0 0
;
M x f x
c. Phương trình của tiếp tuyến:
Định lí 2: Phương trình tiếp tuyến của đồ thị
C
của hàm số
y f x
tại điể
m
0 0 0
;
M x f x
là
0 0
– –
y y f x x x
2. Ý nghĩa vật lí
a. Vận tốc tức thời: Xét chuyển động thẳng xác định bởi phương trình:
s f t
, với
f t
là hàm số có đạo hàm. Khi đó, vận tốc tức thời của chất điểm tại thời điểm
0
t
là
đạo hàm của hàm số
s f t
tại
0
t
.
0 0 0
v t s t f t
b. Cường độ tức thời: Điện lượng
Q
truyền trong dây dẫn xác định bởi phương
trình:
Q f t
, với
f t
là hàm số có đạo hàm. Khi đó, cường độ tức thời của dòng
điện tại thời điểm t
0
là đạo hàm của hàm số
Q f t
tại
0
t
.
0 0 0
I t Q t f t
0
M
M
T
(C)
O
0
f(x )
0
f(x x)
y
x
0
x
0
x x
x
y
0
M
T
(C)
M
Chia sẻ bởi: 
Trịnh Thị Thanh
Trịnh Thị Thanh Liên kết tải về
Tài liệu tự học chủ đề đạo hàm 2,3 MB Tải về
Có thể bạn quan tâm
-
Soạn bài Các loài chung sống với nhau như thế nào? - Kết nối tri thức 6
-
Văn mẫu lớp 12: Dàn ý phân tích sức sống tiềm tàng của Mị (6 Mẫu + Sơ đồ tư duy)
-
Bộ đề thi học kì 2 môn Ngữ văn 7 năm 2023 - 2024 sách Chân trời sáng tạo
-
Bộ đề thi học sinh giỏi môn Ngữ văn lớp 7
-
Văn mẫu lớp 12: Nghị luận xã hội về giờ trái đất (Dàn ý + 7 Mẫu)
-
Văn mẫu lớp 12: Phân tích tình huống truyện Chiếc thuyền ngoài xa
-
Dẫn chứng về Cho và nhận - Ví dụ về Cho và Nhận trong cuộc sống
-
Soạn bài Bức tranh của em gái tôi - Cánh Diều 6
-
Bộ đề thi học kì 2 môn Ngữ văn lớp 7 năm 2023 - 2024 (Sách mới)
-
Văn mẫu lớp 12: Nghị luận xã hội Đời phải trải qua giông tố nhưng không được cúi đầu trước giông tố
Xác thực tài khoản!
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:
Số điện thoại chưa đúng định dạng!
Sắp xếp theo
