Phương pháp tọa độ hóa hình không gian Tọa độ hóa hình học không gian

Giới thiệu Tải về Bình luận

Phương pháp tọa độ hóa hình không gian gồm 16 trang hướng dẫn phương pháp tọa độ hóa để giải các bài toán hình học không gian. Tài liệu bao gồm các kiến thức như: các công thức, cách xác định tọa độ điểm, cách chọn hệ trục tọa độ – chọn véctơ kèm theo các ví dụ minh họa.

Tọa độ hóa hình học không gian được trình bày rất khoa học, logic giúp người học dễ hình dung và hiểu rõ kiến thức. Thông qua tài liệu này các bạn lớp 12 nhanh chóng nắm vững kiến thức để giải nhanh các bài tập hình không gian. Bên cạnh đó các bạn xem thêm bộ đề ôn thi THPT Quốc gia môn Toán, phân dạng câu hỏi và bài tập trong đề thi THPT Quốc gia môn Toán.

Phương pháp tọa độ hóa hình không gian

I. Các công thức tọa độ hóa hình không gian

1. Vectơ trong không gian

Trong không gian cho các vect $\overrightarrow{u_{1}}=\left(x_{1}, y_{1}, z_{1}\right), \overrightarrow{u_{2}}=\left(x_{2}, y_{2}, z_{2}\right)$ $\overrightarrow{u_{1}}=\left(x_{1}, y_{1}, z_{1}\right), \overrightarrow{u_{2}}=\left(x_{2}, y_{2}, z_{2}\right)$ và số k tùy $\hat{y}$ $\hat{y}$

$\begin{array}{l} \overrightarrow{u_{1}}=\overrightarrow{u_{2}} \Leftrightarrow\left\{\begin{array}{l} x_{1}=x_{2} \\ y_{1}=y_{2} \\ z_{1}=z_{2} \end{array}\right. \\ \overrightarrow{u_{1}} \pm \overrightarrow{u_{2}}=\left(x_{1} \pm x_{2}, y_{1} \pm y_{2}, z_{1} \pm z_{2}\right) \end{array}$ $\begin{array}{l} \overrightarrow{u_{1}}=\overrightarrow{u_{2}} \Leftrightarrow\left\{\begin{array}{l} x_{1}=x_{2} \\ y_{1}=y_{2} \\ z_{1}=z_{2} \end{array}\right. \\ \overrightarrow{u_{1}} \pm \overrightarrow{u_{2}}=\left(x_{1} \pm x_{2}, y_{1} \pm y_{2}, z_{1} \pm z_{2}\right) \end{array}$

$k \overrightarrow{u_{1}}=\left(k x_{1}, k y_{1}, k z_{1}\right)$ $k \overrightarrow{u_{1}}=\left(k x_{1}, k y_{1}, k z_{1}\right)$

- Tích có hướng: $\overrightarrow{u_{1}} \cdot \overrightarrow{u_{2}}=x_{1} \cdot x_{2}+y_{1} \cdot y_{2}+z_{1} \cdot z_{2}$ $\overrightarrow{u_{1}} \cdot \overrightarrow{u_{2}}=x_{1} \cdot x_{2}+y_{1} \cdot y_{2}+z_{1} \cdot z_{2}$

- Hai vectơ vuông góc nhau $\Leftrightarrow \overrightarrow{u_{1}} \cdot \overrightarrow{u_{2}}=0 \Leftrightarrow x_{1} \cdot x_{2}+y_{1} \cdot y_{2}+z_{1} \cdot z_{2}=0$ $\Leftrightarrow \overrightarrow{u_{1}} \cdot \overrightarrow{u_{2}}=0 \Leftrightarrow x_{1} \cdot x_{2}+y_{1} \cdot y_{2}+z_{1} \cdot z_{2}=0$

$\left|\overrightarrow{u_{1}}\right|=\sqrt{x_{1}^{2}+y_{1}^{2}+z_{1}^{2}}$ $\left|\overrightarrow{u_{1}}\right|=\sqrt{x_{1}^{2}+y_{1}^{2}+z_{1}^{2}}$

- Gọi $\varphi$ $\varphi$ là góc hợp bởi hai vectơ $\left(0^{\circ} \leqslant \varphi \leqslant 180^{\circ}\right)$ $\left(0^{\circ} \leqslant \varphi \leqslant 180^{\circ}\right)$

$\begin{aligned} \cos \varphi=\cos \left(\overrightarrow{u_{1}}, \overrightarrow{u_{2}}\right)=\frac{\overrightarrow{u_{1}} \cdot \overrightarrow{u_{2}}}{\left|\overrightarrow{u_{1}}\right| \cdot\left|\overrightarrow{u_{2}}\right|}=\frac{x_{1} x_{2}+y_{1} y_{2}+z_{1} z_{2}}{\sqrt{x_{1}^{2}+y_{1}^{2}+z_{1}^{2}} \cdot \sqrt{x_{2}^{2}+y_{2}^{2}+z_{2}^{2}}} \\ \overrightarrow{A B}=\left(x_{B}-x_{A}, y_{B}-y_{A}, z_{B}-z_{A}\right) \\ A B=\sqrt{\left(x_{B}-x_{A}\right)^{2}+\left(y_{B}-y_{A}\right)^{2}+\left(z_{B}-z_{A}\right)^{2}} \end{aligned}$ $\begin{aligned} \cos \varphi=\cos \left(\overrightarrow{u_{1}}, \overrightarrow{u_{2}}\right)=\frac{\overrightarrow{u_{1}} \cdot \overrightarrow{u_{2}}}{\left|\overrightarrow{u_{1}}\right| \cdot\left|\overrightarrow{u_{2}}\right|}=\frac{x_{1} x_{2}+y_{1} y_{2}+z_{1} z_{2}}{\sqrt{x_{1}^{2}+y_{1}^{2}+z_{1}^{2}} \cdot \sqrt{x_{2}^{2}+y_{2}^{2}+z_{2}^{2}}} \\ \overrightarrow{A B}=\left(x_{B}-x_{A}, y_{B}-y_{A}, z_{B}-z_{A}\right) \\ A B=\sqrt{\left(x_{B}-x_{A}\right)^{2}+\left(y_{B}-y_{A}\right)^{2}+\left(z_{B}-z_{A}\right)^{2}} \end{aligned}$

- Tọa độ các điểm đặc biệt:

- Tọa độ trung điểm I của A B: $I\left(\frac{x_{A}+x_{B}}{2}, \frac{y_{A}+y_{B}}{2}, \frac{z_{A}+z_{B}}{2}\right)$ $I\left(\frac{x_{A}+x_{B}}{2}, \frac{y_{A}+y_{B}}{2}, \frac{z_{A}+z_{B}}{2}\right)$

Tọa độ trọng tâm G của tam giác A B C:

$G\left(\frac{x_{A}+x_{B}+x_{C}}{3}, \frac{y_{A}+y_{B}+y_{C}}{3}, \frac{z_{A}+z_{B}+z_{C}}{3}\right.),$ $G\left(\frac{x_{A}+x_{B}+x_{C}}{3}, \frac{y_{A}+y_{B}+y_{C}}{3}, \frac{z_{A}+z_{B}+z_{C}}{3}\right.),$

- Tọa độ trọng tâm G của tứ diện ABCD:

$G\left(\frac{x_{A}+x_{B}+x_{C}+x_{D}}{4}, \frac{y_{A}+y_{B}+y_{C}+y_{D}}{4}, \frac{z_{A}+z_{B}+z_{C}+z_{D}}{4}\right)$ $G\left(\frac{x_{A}+x_{B}+x_{C}+x_{D}}{4}, \frac{y_{A}+y_{B}+y_{C}+y_{D}}{4}, \frac{z_{A}+z_{B}+z_{C}+z_{D}}{4}\right)$

Tích có hướng của hai vectơ là 1 vectơ vuông góc của hai vectơ xác định bởi

$\vec{u}=\left[\overrightarrow{u_{1}}, \overrightarrow{u_{2}}\right]=\left(\left|\begin{array}{ll} y_{1} & z_{1} \\ y_{2} & z_{2} \end{array}\right|,\left|\begin{array}{cc} z_{1} & x_{1} \\ z_{2} & x_{2} \end{array}\right|,\left|\begin{array}{ll} x_{1} & z_{1} \\ x_{2} & z_{2} \end{array}\right|\right)$ $\vec{u}=\left[\overrightarrow{u_{1}}, \overrightarrow{u_{2}}\right]=\left(\left|\begin{array}{ll} y_{1} & z_{1} \\ y_{2} & z_{2} \end{array}\right|,\left|\begin{array}{cc} z_{1} & x_{1} \\ z_{2} & x_{2} \end{array}\right|,\left|\begin{array}{ll} x_{1} & z_{1} \\ x_{2} & z_{2} \end{array}\right|\right)$

- Một số tính chất của tích có hướng

$\star \vec{a}$ $\star \vec{a}$ và $\vec{b}$ $\vec{b}$ cùng phương $\Leftrightarrow[\vec{a}, \vec{b}]=\overrightarrow{0}$ $\Leftrightarrow[\vec{a}, \vec{b}]=\overrightarrow{0}$

A, B, C thẳng hàng $\Leftrightarrow[\overrightarrow{A B}, \overrightarrow{A C}]=\overrightarrow{0}$ $\Leftrightarrow[\overrightarrow{A B}, \overrightarrow{A C}]=\overrightarrow{0}$

Ba vectơ $\vec{a}, \vec{b}, \vec{c}$ $\vec{a}, \vec{b}, \vec{c}$ đồng phẳng $\Leftrightarrow[\vec{a}, \vec{b}] \cdot \vec{c}=0$ $\Leftrightarrow[\vec{a}, \vec{b}] \cdot \vec{c}=0$

Bốn điểm A, B, C, D không đồng phẳng $\Leftrightarrow[\overrightarrow{A B}, \overrightarrow{A C}] \cdot \overrightarrow{A D} \neq \overrightarrow{0}$ $\Leftrightarrow[\overrightarrow{A B}, \overrightarrow{A C}] \cdot \overrightarrow{A D} \neq \overrightarrow{0}$

$\star|[\vec{a}, \vec{b}]|=|\vec{a}| \cdot|\vec{b}| \cdot \sin (\vec{a}, \vec{b})$ $\star|[\vec{a}, \vec{b}]|=|\vec{a}| \cdot|\vec{b}| \cdot \sin (\vec{a}, \vec{b})$

Các ứng dụng của tích có hướng

$\star S_{A B C D}=|[\overrightarrow{A B}, \overrightarrow{A D}]|$ $\star S_{A B C D}=|[\overrightarrow{A B}, \overrightarrow{A D}]|$

$\star$ $\star$Diện tích tam giác: $S_{A B C}=\frac{1}{2}|[\overrightarrow{A B}, \overrightarrow{A C}]|$ $S_{A B C}=\frac{1}{2}|[\overrightarrow{A B}, \overrightarrow{A C}]|$

*Thể tích khối hộp:

$V_{A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}}=\left|[\overrightarrow{A B}, \overrightarrow{A D}] \cdot \overrightarrow{A A^{\prime}}\right|$ $V_{A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}}=\left|[\overrightarrow{A B}, \overrightarrow{A D}] \cdot \overrightarrow{A A^{\prime}}\right|$

*Thể tích tứ diện:

$V_{A B C D}=\frac{1}{6}|[\overrightarrow{A B}, \overrightarrow{A C}] \cdot \overrightarrow{A D}|$ $V_{A B C D}=\frac{1}{6}|[\overrightarrow{A B}, \overrightarrow{A C}] \cdot \overrightarrow{A D}|$

2. Phương trình mặt phẳng

- Phương trình tổng quát $(\alpha): a x+b y+c z+d=0 với \left(a^{2}+b^{2}+c^{2} \neq 0\right).$ $(\alpha): a x+b y+c z+d=0 với \left(a^{2}+b^{2}+c^{2} \neq 0\right).$

- Phương trình mặt phẳng $(\alpha)$ $(\alpha)$ qua $M\left(x_{0}, y_{0}, z_{0}\right)$ $M\left(x_{0}, y_{0}, z_{0}\right)$ và có vectơ pháp tuyến $\vec{n}=(a, b, c)$ $\vec{n}=(a, b, c)$

$(\alpha): a\left(x-x_{0}\right)+b\left(y-y_{0}\right)+c\left(z-z_{0}\right)=0$ $(\alpha): a\left(x-x_{0}\right)+b\left(y-y_{0}\right)+c\left(z-z_{0}\right)=0$

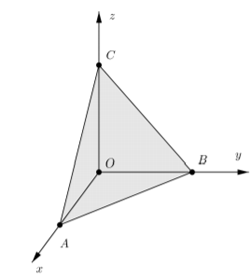
Phương trình mặt phẳng theo đoạn chắn: $(\alpha)$ $(\alpha)$ qua A(a, 0,0) ; B(0, b, 0) ; C(0,0, c)

$(\alpha): \frac{x-x_{0}}{a}+\frac{y-y_{0}}{b}+\frac{z-z_{0}}{c}=1, \quad$ $(\alpha): \frac{x-x_{0}}{a}+\frac{y-y_{0}}{b}+\frac{z-z_{0}}{c}=1, \quad$với $a, b, c \neq 0$ $a, b, c \neq 0$

- Nếu $\vec{n}=(a, b, c)$ $\vec{n}=(a, b, c)$ là vectơ pháp tuyến của $(\alpha)$ $(\alpha)$ thì $k \vec{n}, k \neq 0$ $k \vec{n}, k \neq 0$ cũng là vectơ pháp tuyến của $(\alpha)$ $(\alpha)$. Do đó một mặt phẳng có vô số vectơ pháp tuyến. Trong một số trường hợp ta có thể tìm vectơ pháp tuyến bằng cách chọn một giá trị cụ thể (hoặc b hoặc c) và tính hai giá trị còn lại đảm bảo đúng tỉ lệ a: b: c.

3. Góc

Góc giũa hai mặt phẳng: Cho mặt phẳng $(\alpha)$ $(\alpha)$ có vectơ pháp tuyến là $\overrightarrow{n_{\alpha}}$ $\overrightarrow{n_{\alpha}}$, mặt phẳng $(\beta)$ $(\beta)$ có vectơ pháp tuyến $\overrightarrow{n_{\beta}}$ $\overrightarrow{n_{\beta}}$, khi đó góc giữa $(\alpha)$ $(\alpha)$ và $(\beta)$ $(\beta)$ được tính bằng

$\cos ((\alpha),(\beta))=\left|\cos \left(\overrightarrow{n_{\alpha}}, \overrightarrow{n_{\beta}}\right)\right|=\frac{\left|\overrightarrow{n_{\alpha}} \cdot \overrightarrow{n_{\beta}}\right|}{\left|\overrightarrow{n_{\alpha}}\right| \cdot\left|\overrightarrow{n_{\beta}}\right|}$ $\cos ((\alpha),(\beta))=\left|\cos \left(\overrightarrow{n_{\alpha}}, \overrightarrow{n_{\beta}}\right)\right|=\frac{\left|\overrightarrow{n_{\alpha}} \cdot \overrightarrow{n_{\beta}}\right|}{\left|\overrightarrow{n_{\alpha}}\right| \cdot\left|\overrightarrow{n_{\beta}}\right|}$
Góc giữa hai đường thẳng: Cho hai đường thẳng $d_{1}$ $d_{1}$ và $d_{2}$ $d_{2}$ có các vectơ chỉ phương là $\overrightarrow{u_{1}}$ $\overrightarrow{u_{1}}$ và $\overrightarrow{u_{2}}$ $\overrightarrow{u_{2}}$, khi đó góc giữa $d_{1}$ $d_{1}$ và $d_{2}$ $d_{2}$ tính bằng

$\cos \left(d_{1}, d_{2}\right)=\left|\cos \left(\overrightarrow{u_{2}}, \overrightarrow{u_{2}}\right)\right|=\frac{\left|\overrightarrow{u_{1}} \cdot \overrightarrow{u_{2}}\right|}{\left|\overrightarrow{u_{1}}\right| \cdot\left|\overrightarrow{u_{2}}\right|}$ $\cos \left(d_{1}, d_{2}\right)=\left|\cos \left(\overrightarrow{u_{2}}, \overrightarrow{u_{2}}\right)\right|=\frac{\left|\overrightarrow{u_{1}} \cdot \overrightarrow{u_{2}}\right|}{\left|\overrightarrow{u_{1}}\right| \cdot\left|\overrightarrow{u_{2}}\right|}$

2. Xác định tọa độ điểm

2.1 Tọa độ điểm trên trục tọa độ

Tìm tọa độ điểm A trên trục tọa độ ta tìm khoảng cách từ A đến gốc tọa độ và dựa vào chiều dương đã chọn để xác định tọa độ A.

Ví dụ chọn tia O A trùng tia O x , điểm A và B nằm trên O x

• O A = 2 ⇒ A (0, 0, 2).

• O B = 3 ⇒ B (0, 0,−3) (do B nằm ở phần âm)

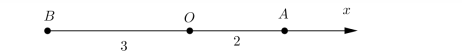
2.2 Tọa độ điểm trên mặt phẳng tọa độ

Tìm tọa độ của A trên 1 mặt phẳng tọa độ ta tìm hình chiếu của A trên các trục tọa
độ và dựa vào các tọa độ hình chiếu này để xác định tọa độ A.

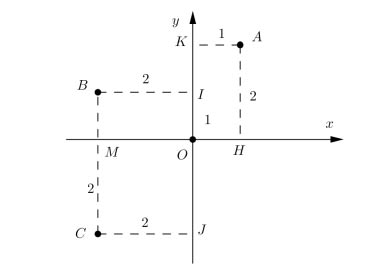
Ví dụ các điểm A,B,C có hình chiếu trên các trục với độ dài như hình vẽ, theo chiều dương
đã chọn ta được

• AK = 1 = x_K , AH = 2 = y_K : tọa độ A(1, 2)

• B I = 2 = −x_B (do B nằm phần âm của trục hoành),BM = 1 = yB : tọa độ B(−2, 1)

• C J = 2,C M = 2: tọa độ C (−2,−2) (do C nằm ở phần âm của trục tung và trục hoành)

2.3 Tọa độ điểm trường hợp tổng quát

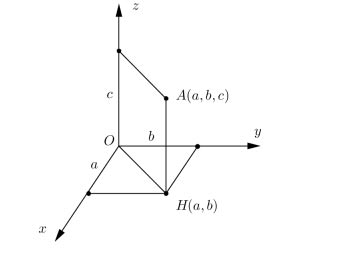
Tìm tọa độ của A đầu tiên ta tìm tọa độ hình chiếu H của A lên mặt phẳng tọa độ bất kì, sau đó ta tính độ dài AH . Tọa độ A xác định nhờ tọa độ H và độ dài AH .

Ví dụ tọa độ hình chiếu vuông góc của A lên mặt phẳng Oxy là H (a,b ), ta tính được AH = c thì khi đó A có tọa độ A(a,b, c ) (giả sử rằng các thành phần tọa độ A đều nằm trong phần
dương).