Phương pháp giải các dạng toán chuyên đề tam giác Tài liệu ôn tập lớp 7 môn Toán
Mời quý thầy cô cùng các bạn học sinh lớp 7 tham khảo tài liệu Phương pháp giải các dạng toán chuyên đề tam giác được Eballsviet.com đăng tải trong bài viết dưới đây.
Tài liệu bao gồm 48 trang, tổng hợp lý thuyết SGK, phân dạng và hướng dẫn giải các dạng toán chuyên đề tam giác trong chương trình Hình học lớp 7. Nội dung tài liệu bao gồm phương pháp giải các dạng toán chuyên đề tam giác như:
- Tổng ba góc của một tam giác.
- Hai tam giác bằng nhau.
- Trường hợp bằng nhau thứ nhất của tam giác cạnh - cạnh - cạnh.
- Trường hợp bằng nhau thứ hai của tam giác cạnh - góc - cạnh.
- Trường hợp bằng nhau thứ ba của tam giác góc - cạnh - góc.
- Tam giác cân
- Định lý Py-ta-go
- Các trường hợp bằng nhau của tam giác vuông
Phương pháp giải các dạng toán chuyên đề tam giác.
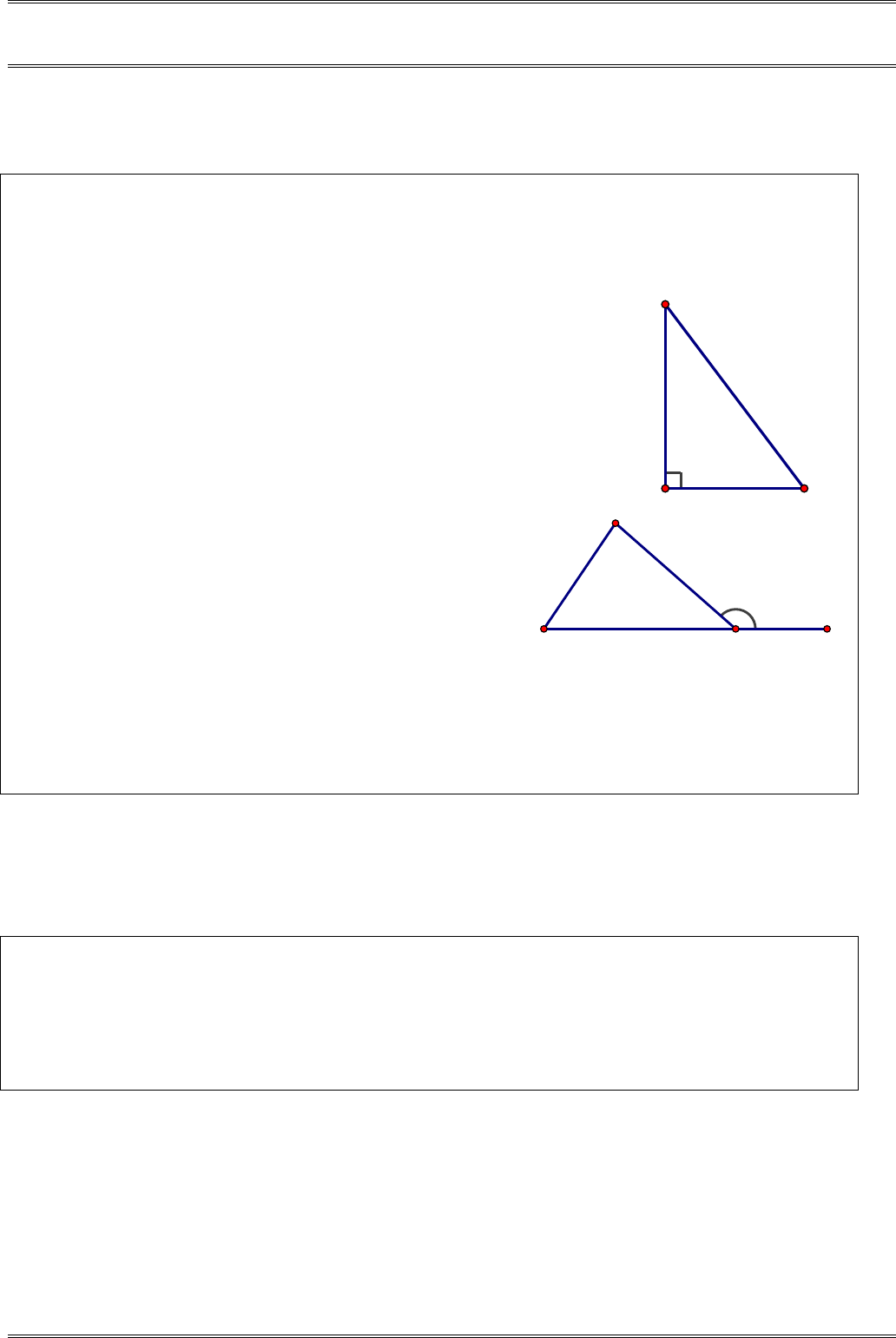
§ 8. TỔNG BA GÓC CỦA MỘT TAM GIÁC
A. TÓM TẮT LÝ THUYẾT
1. Tổng ba góc của một tam giác.
Tổng ba góc của một tam giác bằng
180 .°
180ABC A B C∆ ⇒++= °
2. Áp dụng vào tam giác vuông
a) Định nghĩa: Tam giác vuông là tam giác có một góc vuông.
b) Tính chất: Trong tam giác vuông, hai góc nhọn phụ nhau
90
90
ABC
BC
A
∆
⇒+=°
= °
3. Góc ngoài của
tam giác
a) Định nghĩa: Góc ngoài của tam giác là góc kề
bù với một góc của tam giác.
b) Tính chất:
• Mỗi góc ngoài của một tam giác bằng tổng hai
góc trong không kề với nó.
.ACD A B= +
• Góc ngoài của tam giác lớn hơn mỗi góc trong
không kề với nó.
,ACD A>
.ACD B>
B. CÁC DẠNG TOÁN
Dạng 1. TÍNH SỐ ĐO GÓC CỦA MỘT TAM GIÁC
Phương pháp giải.
• Lập các đẳng thức thể hiện:
- Tổng ba góc của tam giác bằng
180 .°
- Trong tam giác vu
ông, hai góc nhọn phụ nhau.
- Góc ngoài của tam giác bằng tổng hai góc trong không kề với nó.
• Sau đó tính số đo của góc phải tìm.
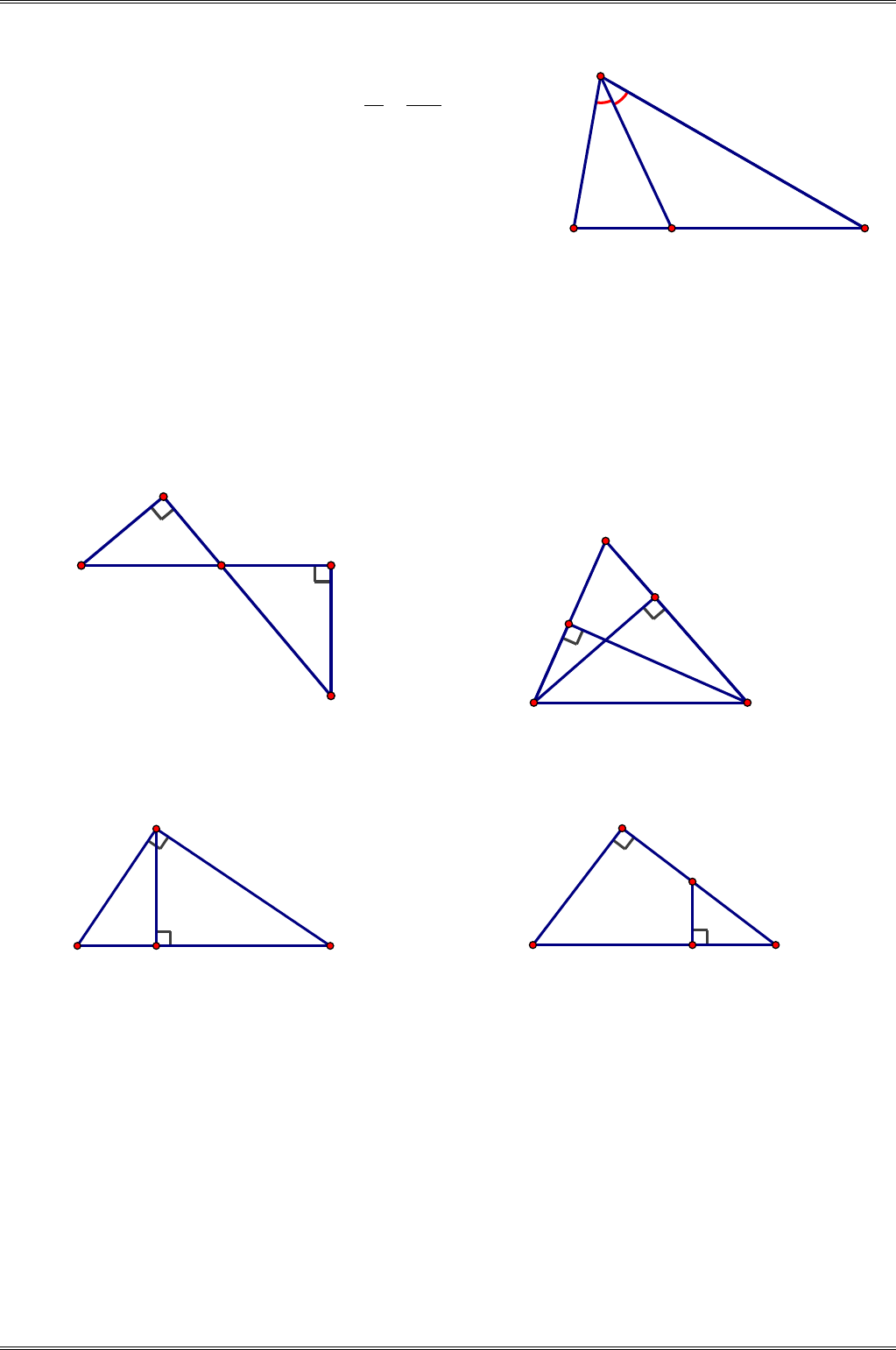
Ví dụ 1. (Bài 1 tr.108 SGK)
Cho tam giác
ABC
có
80 ,B = °
30 .C = °
Tia phân giác của góc
A
cắt
BC
ở
D
. Tính
,ADC
.ADB
Hướng dẫn.
A
C
B
B
D
A
C
-180-
CHUYÊN ĐỀ TAM GIÁC
:ABC∆
180ABC++= °
80 30 180A⇒ + °+ °= °
70A⇒=°
Do đó
12
70
35 .
22
A
AA
°
= = = = °
Góc ngoài
1
ADC B A= +
80 35 115= °+ °= °
(góc ngoài của
ABD∆
).
Suy ra
180 115 65 .ADB = °− °= °
Ví dụ 2. (Bài 6 tr.109 SGK)
Tìm số đo
x
ở các hình
55,
56,
57,
58
(SGK)
Hình 55
(SGK) Hình 56 (SGK)
Hình 57 (SGK) Hình 58 (SGK)
Giải.
a)
( )
12
90 40 .AI BI AB x+ = + = ° ⇒ = ⇒ °=
b)
( )
90 25 .ABD A ACE A ABD ACE x+= +==°⇒ = ⇒= °
c)
1
1
90
60 .
90
IMP M
IMP N x
NM
+=°
⇒ = ⇒= °
+=°
x
2
1
I
B
A
K
H
25
°
x
D
A
B
C
E
x
60
°
1
D
B
C
A
x
55
°
B
A
E
H
K
2
1
30
°
80
°
D
A
B
C
-181-
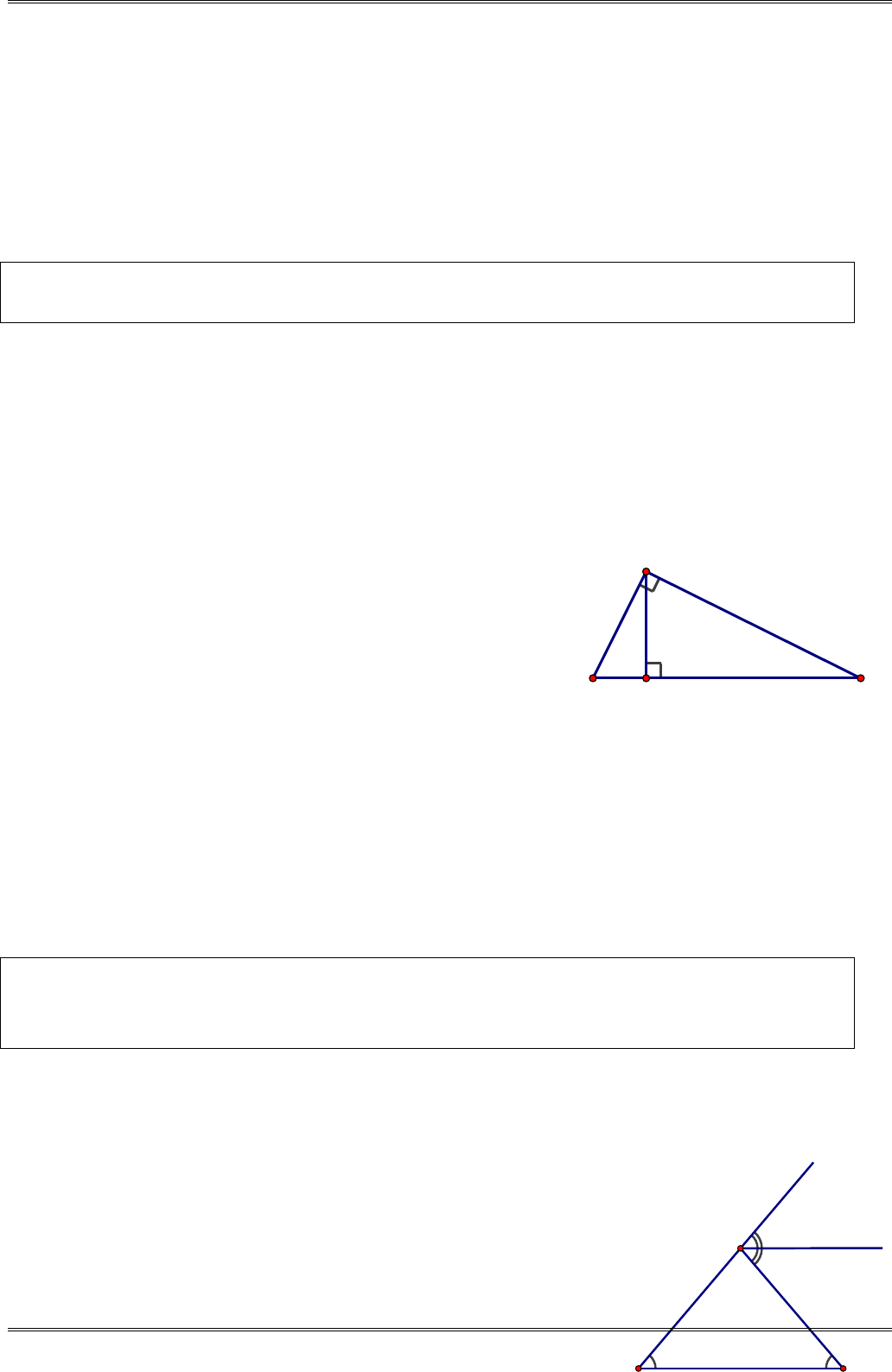
d)
90 90 90 55 35 .AE E A+ = °⇒ = °− = °− °= °
90 35 125 .x BKE E= + = °+ °= °
Dạng 2. NHẬN BIẾT MỘT TAM GIÁC VUÔNG, TÌM CÁC GÓC BẰNG NHAU TRONG
HÌNH VẼ CÓ TAM GIÁC VUÔNG.
Phương pháp giải.
Để nhận biết tam giác vuông, ta chứng minh tam giác đó có một góc bằng
90 .°
Trong hình
vẽ có tam giác vuông, cần chú ý rằng hai góc nhọn của tam giác vuông phụ nhau.
Ví dụ 3. (Bài 7 tr.109 SGK)
Cho tam giác
ABC
vuông tại
A
. Kẻ
AH
vuông góc với
BC
( )
H BC∈
a
)
T
ìm các cặp góc phụ nhau trong hình vẽ.
b) Tì
m các cặp góc nhọn bằng nhau trong hình vẽ.
Hướng dẫn.
a)
C
ác cặp góc phụ nhau:
1
A
và
2
,A
B
và
,C
B
và
1
,A
C
và
2
.A
b) Các c
ặp góc nhọn bằng nhau:
1
CA=
(cùng phụ với
2
A
)
2
BA=
(cùng phụ với
1
A
).
Dạng 3. CHỨNG MINH HAI ĐƯỜNG THẲNG SONG SONG BẰNG CÁCH CHỨNG
MINH HAI GÓC BẰNG NHAU
Phương pháp giải.
Chứng minh hai góc bằng nhau bằng cách chứng tỏ chúng cùng bằng, cùng phụ, cùng bù với
một góc thứ ba (hoặc với hai góc bằng nhau). Từ chứng minh hai góc bằng nhau, ta chứng
minh được hai đường thẳng song song.
Ví dụ 4. (Bài 8 tr.109 SGK)
Cho tam giác
ABC
có
40 .BC= = °
Gọi
Ax
là tia phân giác của góc ngoài ở đỉnh
.A
Hãy chứng tỏ rằng
// .Ax BC
Hướng dẫn.
40 40 80 ,CAD B C= + = °+ °= °
2
1
H
B
C
A
2
1
x
D
B
C
A
-182-
Chia sẻ bởi: 
Trịnh Thị Thanh
Trịnh Thị Thanh Liên kết tải về
Link Download chính thức:
Phương pháp giải các dạng toán chuyên đề tam giác Download
Có thể bạn quan tâm
-
Văn mẫu lớp 9: Đóng vai ngư dân kể lại bài thơ Đoàn thuyền đánh cá
-
Bài thơ Lượm - Sáng tác năm 1949, Tố Hữu
-
Mẫu 09/ĐK: Đơn đăng ký biến động đất đai
-
Tranh tô màu Pikachu - Bộ tranh tô màu Pikachu đẹp
-
Giáo án Toán lớp 1 (Sách mới) - Giáo án Toán lớp 1 (trọn bộ 5 sách)
-
Tuyển tập đề thi học sinh giỏi môn Toán lớp 3
-
Thuyết minh về Thành Cổ Loa (2 Dàn ý + 5 mẫu)
-
Bộ tranh tô màu chủ đề gia đình cho bé
-
Văn mẫu lớp 10: Phân tích tác phẩm Hiền tài là nguyên khí của quốc gia (2 Dàn ý + 10 Mẫu)
-
Những vần thơ hay - Tuyển tập những bài thơ hay
Sắp xếp theo
