Phương pháp giải các dạng toán chuyên đề số hữu tỉ, số thực Ôn tập môn Toán lớp 7 chương 1
Với mong muốn đem đến cho các bạn học sinh lớp 7 có thêm nhiều tài liệu học tập môn Toán, Eballsviet.com giới thiệu tài liệu Phương pháp giải các dạng toán chuyên đề số hữu tỉ, số thực.
Đây là tài liệu cực kì hữu ích, gồm 42 trang tổng hợp lý thuyết trong sách giáo khoa, phân dạng và hướng dẫn giải các dạng toán chuyên đề số hữu tỉ – số thực trong chương trình Đại số 7 chương 1. Hi vọng với tài liệu này các bạn có thêm nhiều tư liệu tham khảo, củng cố kiến thức để đạt được kết quả cao trong các bài kiểm tra, bài thi học kì 1 sắp tới. Ngoài ra các bạn tham khảo thêm tài liệu Tổng hợp bài tập Chương I môn Toán lớp 7. Mời các bạn cùng theo dõi và tải tài liệu tại đây.
Phương pháp giải dạng toán chuyên đề số hữu tỉ, số thực
CHUYÊN ĐỀ SỐ HỮU TỈ - SỐ THỰC
ĐẠI SỐ 7
§1. TẬP HỢP Q
CÁC SỐ HỮU TỈ
A. TÓM T
ẮT LÝ THUYẾT
1. Số hữ
u tỉ là số viết được dưới dạng phân số
a
b
với
, , ab b0
2. Ta có
thể biểu diễn mọi số hữu tỉ trên trục số. Trên chục số, điểm biểu diễn số hữu tỉ
được gọi là điểm
x
3. Với
hai số hữu tỉ bất kỳ
,xy
ta luôn có hoặc
xy
hoặc
xy
hoặc
xy
. Ta có thể so
sánh hai số hữu tỉ bằng cách viết chúng dưới dạng phân số rồi so sánh hai phân số đó.
• Nếu
xy
thì trên trục số, điểm
x
ở bên trái điểm
;y
• Số
hữu tỉ lớn hơn 0 được gọi là số hữu tỉ dương;
• Số hữu tỉ nhỏ hơn 0 được gọi là số hữu tỉ âm;
• Số hữu tỉ 0 không là số hữu tỉ dương cũng không là số hữu tỉ âm.
B. CÁC DẠNG TOÁN
Dạng 1. SỬ DỤNG CÁC KÍ HIỆU
, , , , , .
Phươ
ng pháp giải.
Cần nắm vững ý nghĩa của từng ký hiệu:
• Kí hiệu
đọc là “phần tử của” hoặc “thuộc”.
• Kí hiệu
đọc là “không phải là phần tử của” hoặc “khồng thuộc”.
• Kí hiệu
đọc là “là tập hợp con của”.
• Kí hiệu
chỉ tập hợp các số tự nhiên.
• Kí hiệu
chỉ tập hợp các số nguyên.
• Kí hiệu
chỉ tập hợp các số hữu tỉ.
Ví dụ 1.
(Bài 1 tr.7 SGK)
Điền ký hiệu
, ,
thích hợp vào ô trống:
-3
; -3
; -3
2
3
;
2
3
;
Giả
i
-3
; -3
; -3
2
3
;
2
3
;
Dạng 2. BIỂU DIỄN SỐ HỮU TỈ
Phương pháp giải.
•
S
ố hữu tỉ thường được biểu diễn dưới dạng phân số tối giản.
• Khi biểu diến số hữu tỉ trên trục số, ta thường viết số đó dưới dạng phân số tối giản có
mẫu dương. Khi đó mẫu cửa phân số cho biết đoạn thẳng đơn vị cần được chia thành bao
nhiêu phần bằng nhau.
Ví dụ 2. (Bài 2 tr.7 SGK)
a) Trong các phân số sau, những phân số nào biểu diễn số hữu tỉ
3
4
:
, , , , ?
12 15 24 20 27
15 20 32 28 36
b) Bi
ểu diễn số hữu tỉ
3
4
trên trục số.
Giải
a) Ta có
.
33
44
Rút gọn các phân số đã cho ta được:
; ; ; ; .
12 4 15 3 24 3 20 5 27 3
15 5 20 4 32 4 28 7 36 4
Vậy các phân số biểu diễn số hữu tỉ
3
4
là:
;
15 24
20 32
và
27
36
b) Bi
ểu diễn số hữu tỉ
3
4
trên trục số: Ta viết
33
44
và biểu diễn trên trục số như sau:
Dạng 3. SO SÁNH CÁC SỐ HỮU TỈ
Phương pháp giải.
• Viết các số hữu tỉ dưới dạng phân số có cùng một mẫu dương;
• So sánh các tử, phân số nào tử nhỏ hơn thì phân số đó nhỏ hơn.
• Có thể sử dụng tính chất sau để so sánh: Nếu
, , abc
và
ab
thì
.acbc
Ví dụ 3. (Bài 3 tr.8 SGK)
So sánh các số hữu tỉ:
a)
x
2
7
và
;y
3
11
b)
x
213
300
và
;y
18
25
c)
,x 0 75
và
;y
3
4
Giải
a)
; .xy
2 2 22 3 21
7 7 77 11 77
22 21
và
77 0
nên
22 21
77 77
hay
( ).xy
23
7 11
b)
; .xy
213 18 18 216
300 25 25 300
Ta có:
213 216
300 300
hay
( ).xy
213 18
300 25
Ví dụ 4. (Bài 4 tr.8 SGK)
So sánh số hữu tỉ
( , , )
a
ab b
b
0
với số 0 khi
,ab
cùng dấu và khi
,ab
khác dấu.
Giải
Nhờ tính chất cơ bản của phân số, ta luôn có thể viết một phân số có mẫu âm thành một phân số
bằng nó và có mẫu dương. Vì vậy, ta chỉ cần nhận xét số hữu tỉ
( , , ).
a
ab b
b
0
Nếu cùng dấ
u thì ta có
.a 0
Do đó
a
bb
0
hay
.
a
b
0
Nếu
,ab
khác dấu thì ta có
.a 0
Do đó
a
bb
0
hay
.
a
b
0
Nhận x
ét: Số hữu tỉ
( , , )
a
ab b
b
0
là số dương nếu
,ab
cùng dấu, là số âm nếu
,ab
khác dấu, bằng 0 nếu
.a 0
Ví dụ 5. (Bài 5 tr.8 SGK)
Chia sẻ bởi: 
Trịnh Thị Thanh
Trịnh Thị Thanh Liên kết tải về
Phương pháp giải các dạng toán chuyên đề số hữu tỉ, số thực 1,4 MB Tải về
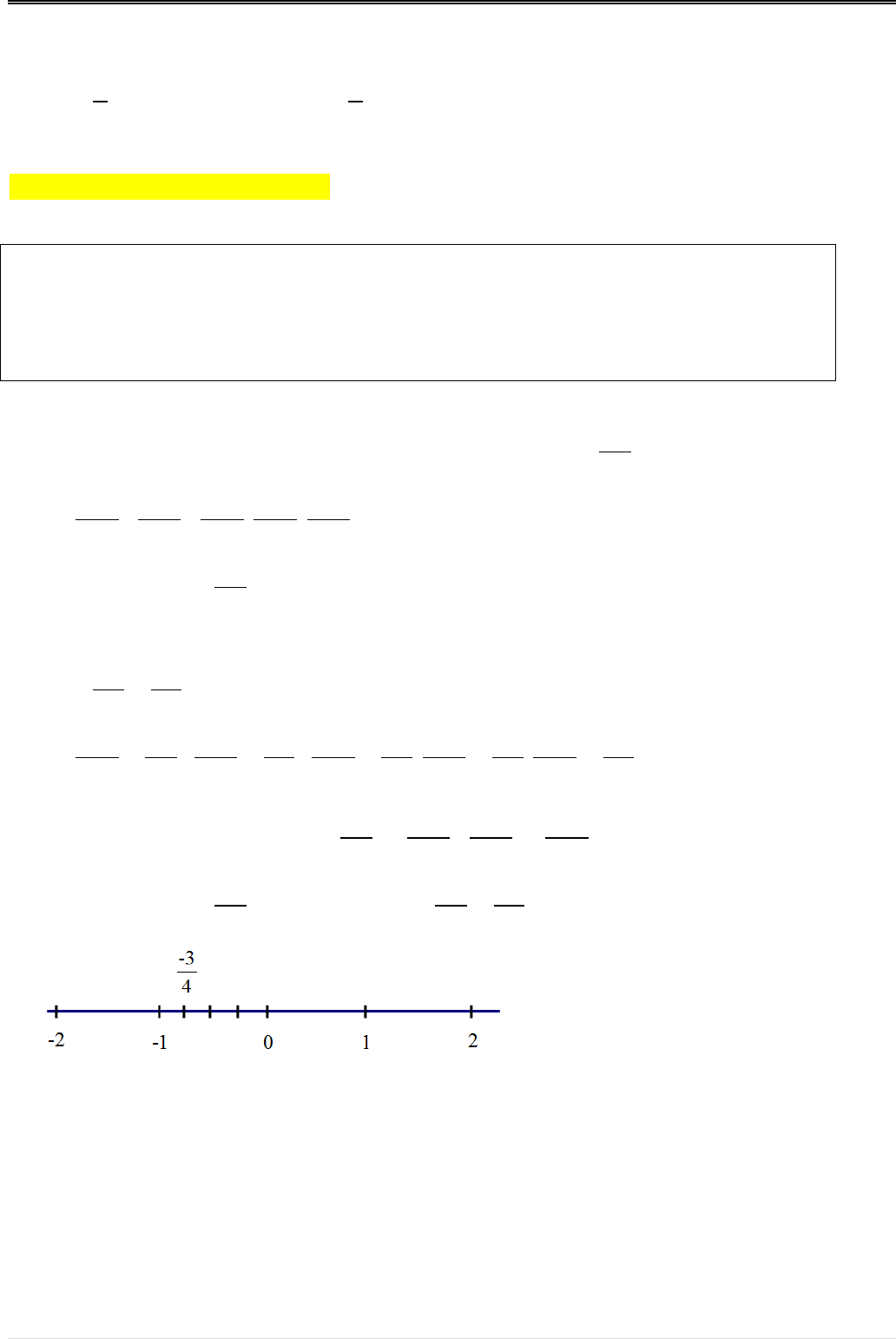
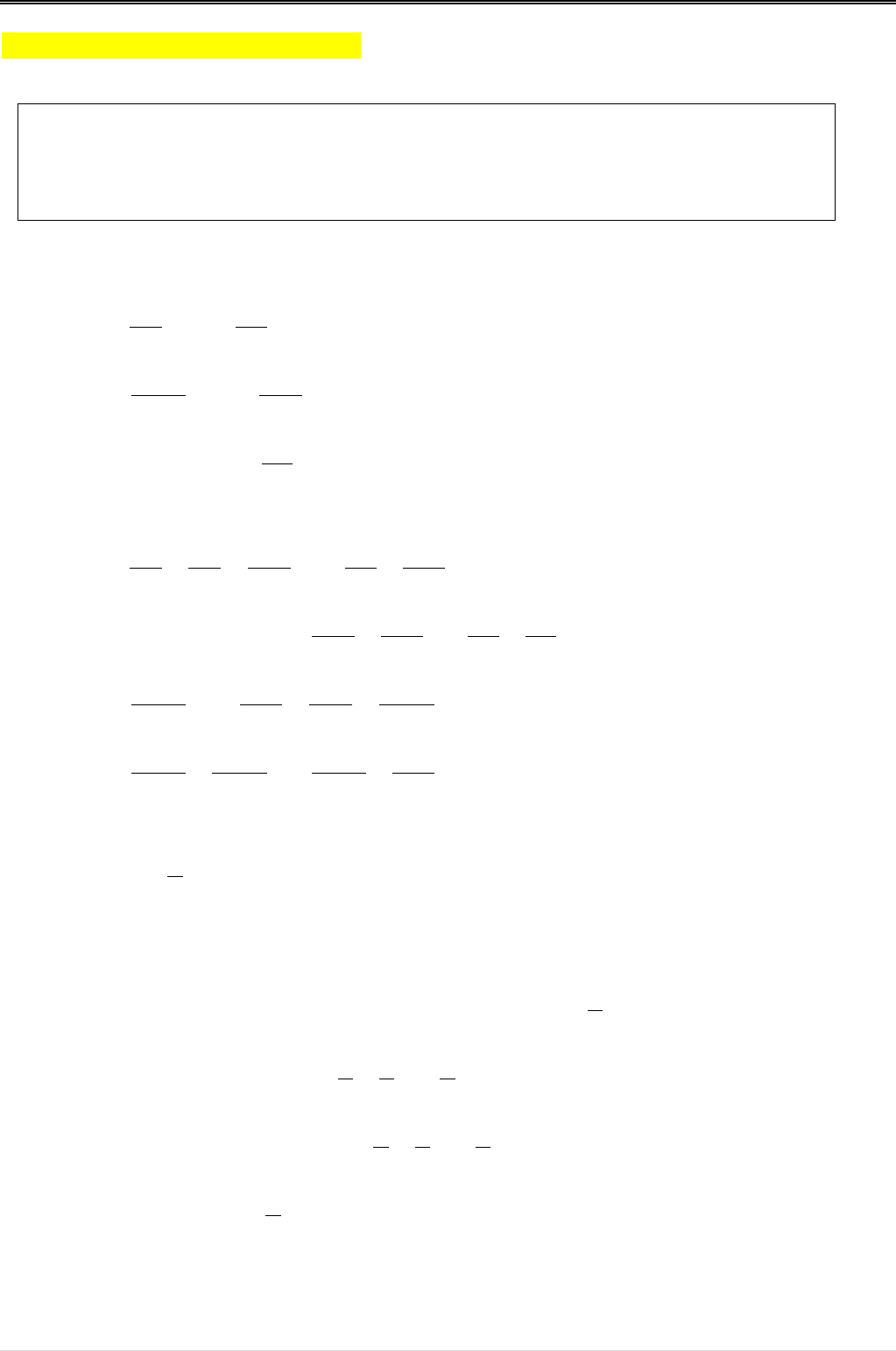
Có thể bạn quan tâm
-
Văn mẫu lớp 12: Dàn ý phân tích nhân vật người đàn bà hàng chài (11 Mẫu + Sơ đồ tư duy)
-
Phân tích tác phẩm Giàn bầu trước ngõ của Nguyễn Ngọc Tư
-
Văn mẫu lớp 12: Phân tích nhân vật Trương Ba trong Hồn Trương Ba da hàng thịt
-
Phân tích nhân vật bé Em trong truyện Áo Tết
-
Văn mẫu lớp 12: Phân tích bi kịch của Trương Ba trong tác phẩm Hồn trương ba, da hàng thịt
-
Văn mẫu lớp 12: Nghị luận về ý thức tôn trọng người khác (2 Dàn ý + 14 mẫu)
-
Văn mẫu lớp 9: Phân tích khổ cuối bài Sang thu của Hữu Thỉnh (Sơ đồ tư duy)
-
Văn mẫu lớp 9: Nghị luận ý nghĩa của sự lắng nghe
-
Văn mẫu lớp 12: Tổng hợp mở bài về tác phẩm Chiếc thuyền ngoài xa (71 mẫu)
-
Kể về một việc làm tốt của em (79 mẫu)
Xác thực tài khoản!
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:
Số điện thoại chưa đúng định dạng!
Sắp xếp theo
