Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao Tài liệu ôn tập môn Toán lớp 12
Mời quý thầy cô cùng các bạn học sinh lớp 12 tham khảo tài liệu Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao được Eballsviet.com đăng tải ngay sau đây.
Đây là tài liệu vô cùng hữu ích, hướng dẫn giải 65 bài toán số phức hay và khó, các bài toán số phức liên quan đến min – max, bất đẳng thức. Sau đây là nội dung chi tiết mời các bạn cùng tải tài liệu tại đây.
Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao
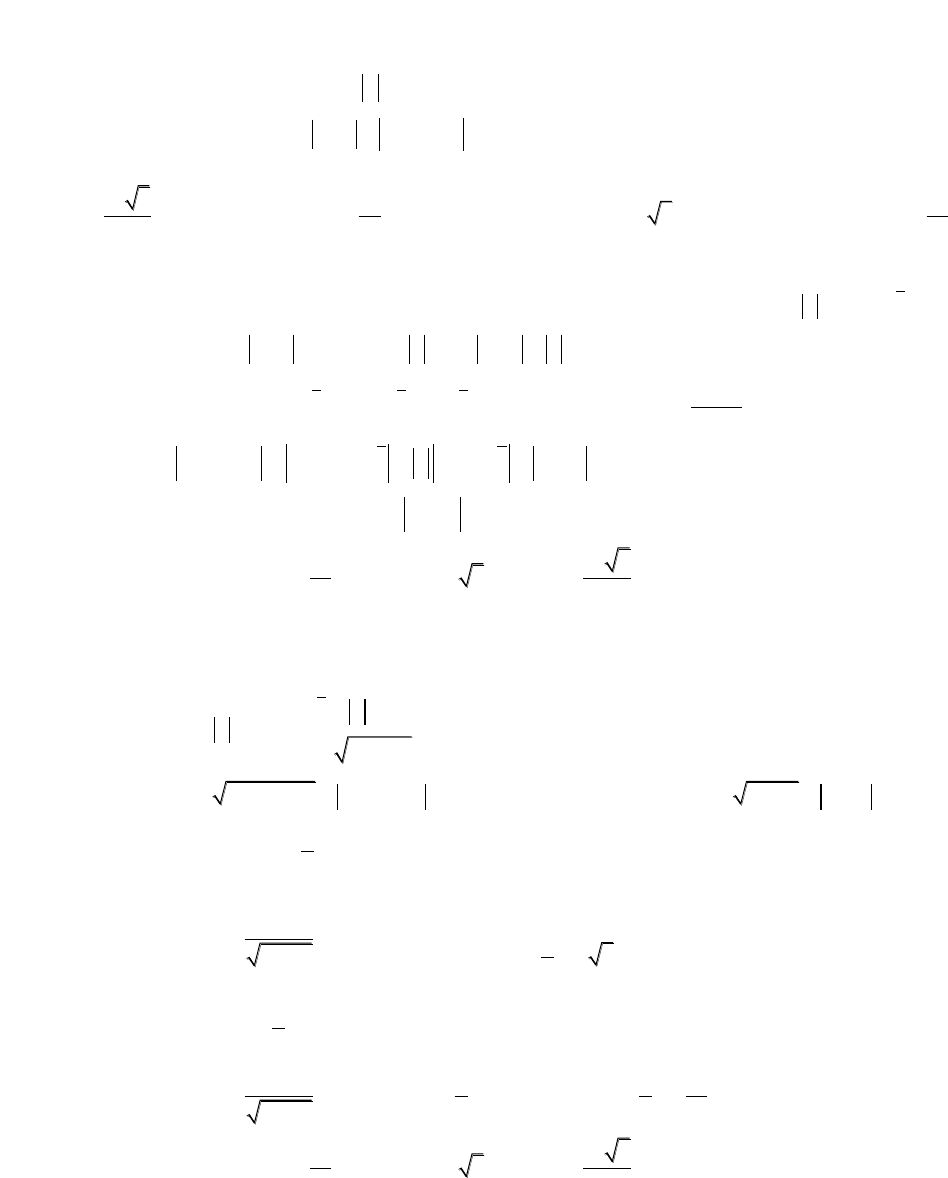
Bài 1: Cho số phức z thỏa mãn
1z
. Gọi M và m lần lượt là giá trị lớn nhất và giá trị
nhỏ nhất của biểu thức
2
11P z z z
. Tính giá trị của M.n
A.
13 3
4
B.
39
4
C.
33
D.
13
4
Cách 1:
Re( )z
là phần thực của số phức z, Im(z) là phần ảo của số phức z,
1 . 1 z z z
Đặt
1tz
, ta có:
0 1 1 1 2 0;2z z z t
2
2
2
1 1 1 . 2 2Re( ) Re( )
2
t
t z z z z z z z z
2 2 2
1 . 1 3z z z z z z z z z t
Xét hàm số:
2
3 , 0;2f t t t t
. Xét 2 TH:
13
4
Maxf t
;
3Minf t
13 3
.
4
Mn
Cách 2:
cos sinz r x i x a bi
Do
2
22
.1
1
1
z z z
z
r a b
2 2cos 2cos 1P x x
, đặt
cos 1;1tx
2 2 2 1f t t t
TH1:
1
1;
2
t
13
1
' 2 0
1
3
22
2
maxf t f
ft
minf t f
t
TH1:
1
;1
2
t
1 7 7 13
' 2 0
8 8 4
22
f t t maxf t f
t
13
4
Maxf t
;
3Minf t
13 3
.
4
Mn
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao
Biên soạn: Phạm Minh Tuấn - TOANMATH.com
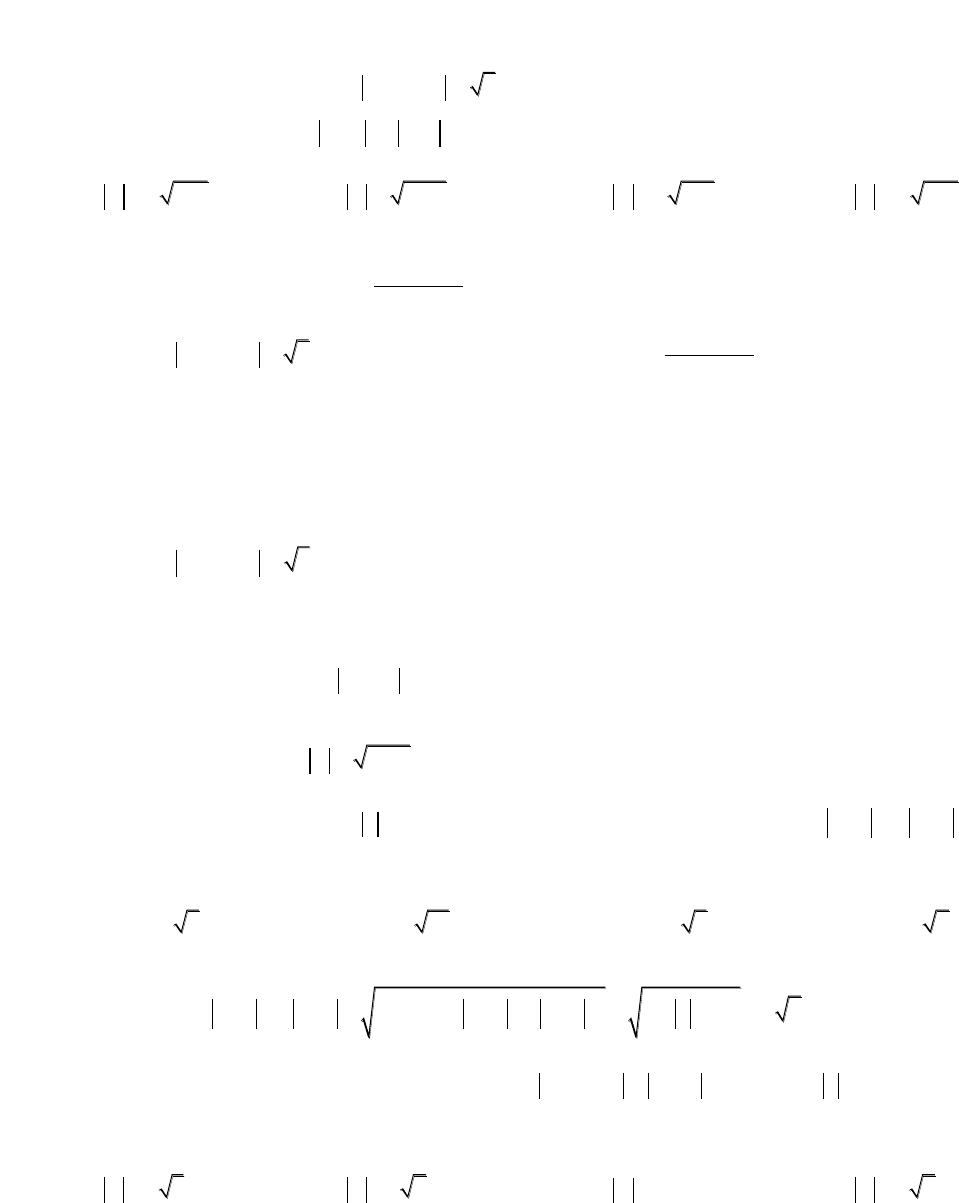
Bài 2: Cho số phức z thỏa mãn
3 4 5zi
. Gọi M và m là giá trị lớn nhất và giá trị
nhỏ nhất của biểu thức
22
2P z z i
. Tính module số phức
w M mi
.
A.
2 314w
B.
1258w
C.
3 137w
D.
2 309w
Cách 1:
43
4 2 3
2
Px
P x y y
2
2 2 2
43
3 4 5 3 4 5 3 4 5
2
Px
z i x y x f x
' 8 3 8 4 11 0 0,2 1,6 0,1 1,7f x x P x x P y P
Thay vào
fx
ta được:
22
33
0,2 1,6 3 0,1 1,7 4 5 0
13
P
PP
P
Cách 2:
22
3 4 5 3 4 5:z i x y C
( ):4 2 3 0x y P
Tìm P sao cho đường thẳng
và đường tròn
C
có điểm chung
; 23 10 13 33d I R P P
Vậy
33MaxP
;
13MinP
33 13 1258w i w
Bài 3: Cho số phức z thỏa mãn
1z
. Tìm giá trị lớn nhất của biểu thức
1 2 1P z z
.
A.
max
25P
B.
max
2 10P
C.
max
35P
D.
max
32P
Giải: Theo BĐT Bunhiacopxki:
2 2 2
22
1 2 1 1 2 1 1 10 1 2 5P z z z z z
Bài 4: Cho số phức
z x yi
,x y R
thỏa mãn
2 4 2z i z i
và
m min z
. Tính
module số phức
w m x y i
.
A.
23w
B.
32w
C.
5w
D.
26w
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao
Biên soạn: Phạm Minh Tuấn - TOANMATH.com
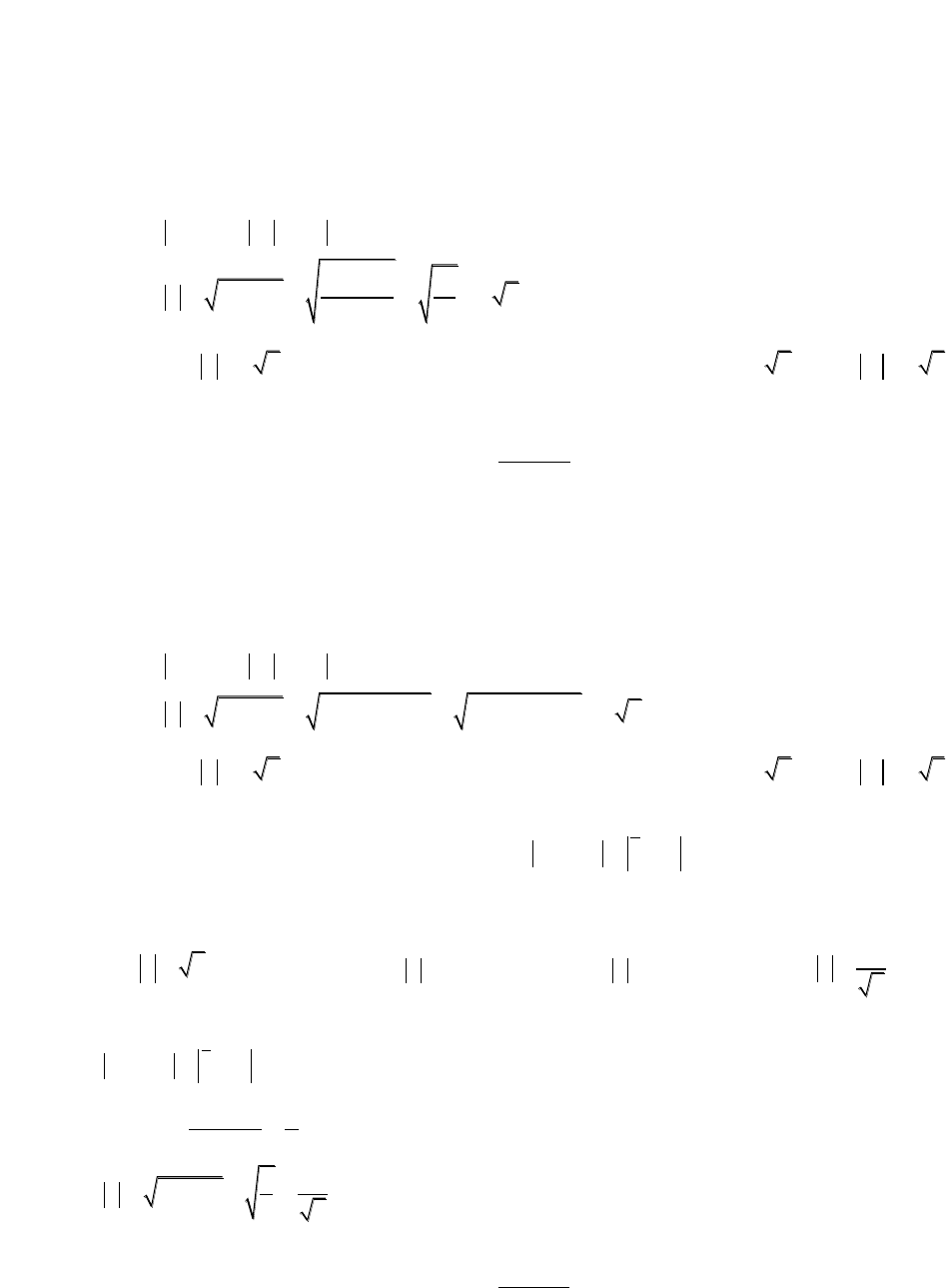
Cách 1:
2 4 2 4z i z i x y
2
2
22
4
22
22
xy
z x y
22min z
, Dấu “=” xảy ra khi
42
w 2 2 4 w 2 6
2
x y x
i
x y y
Chú ý: Với mọi x, y là số thực ta có:
2
22
2
xy
xy
Dấu “=” xảy ra khi
xy
Cách 2:
2 4 2 4z i z i y x
22
2 2 2
4 2 2 8 2 2z x y x x x
22min z
. Dấu “=” xảy ra khi
42
w 2 2 4 w 2 6
22
x y x
i
xy
Bài 5: Cho số phức
z x yi
,x y R
thỏa mãn
12z i z i
. Tìm môđun nhỏ nhất
của z.
A.
2min z
B.
1min z
C.
0min z
D.
1
2
min z
Cách 1:
1 2 1z i z i x y
2
22
1
22
xy
xy
22
11
2
2
z x y
Chú ý: Với mọi x, y là số thực ta có:
2
22
2
xy
xy
Cách 2:
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao
Biên soạn: Phạm Minh Tuấn - TOANMATH.com
Chia sẻ bởi:
Trịnh Thị Thanh
Trịnh Thị Thanh
Liên kết tải về
Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao
2,5 MB
Tải về
Có thể bạn quan tâm
-
Văn mẫu lớp 9: Tổng hợp những kết bài Bài thơ về tiểu đội xe không kính (66 mẫu)
-
Nghị luận xã hội về vai trò của nguồn nước sạch (Dàn ý + 11 mẫu)
-
Văn mẫu lớp 9: Tổng hợp những mở bài Bài thơ về tiểu đội xe không kính (66 mẫu)
-
Đoạn văn nghị luận về tình bạn (Dàn ý + 30 mẫu)
-
Mẫu nhận xét học bạ theo Thông tư 22
-
Nghị luận xã hội về giá trị của bản thân (Dàn ý + 28 Mẫu)
-
Biểu đồ miền: Dấu hiệu nhận biết và cách vẽ biểu đồ miền
-
Phiếu góp ý sách giáo khoa lớp 4 bộ Kết nối tri thức với cuộc sống
-
Phân tích bài thơ Nụ cười xuân của Xuân Diệu
-
Phân tích tác phẩm Hoa đào nở trên vai của Vũ Thị Huyền Trang
Xác thực tài khoản!
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:
Số điện thoại chưa đúng định dạng!
Sắp xếp theo
Mới nhất trong tuần
Đóng
Chỉ thành viên Download Pro tải được nội dung này!
Download Pro - Tải nhanh, website không quảng cáo!
Tìm hiểu thêm