Hướng dẫn giải bài toán cực trị số phức Tài liệu ôn thi THPT Quốc gia 2019 môn Toán
Dưới đây Eballsviet.com xin giới thiệu đến quý thầy cô và các em học sinh, đặc biệt là học sinh lớp 12 tài liệu Hướng dẫn giải bài toán cực trị số phức.
Tài liệu gồm 11 trang trình bày 2 phương pháp giải bài toán cực trị số phức – một dạng toán số phức vận dụng cao trong chương trình Giải tích 12 chương 4. Tài liệu giúp thầy cô giáo có thêm nhiều tư liệu ra đề thi cũng như ôn luyện cho các em. Đồng thời giúp các em học sinh luyện và nâng cao kỹ năng giải toán. Mời các bạn cùng tham khảo và tải tài liệu tại đây.
Hướng dẫn giải bài toán cực trị số phức
Lương Đức Trọng - ĐHSPHN (SĐT:0982715678)
CỰC TRỊ SỐ PHỨC
A. TÓM TẮT LÝ THUYẾT
1. Bất đẳng thức tam giác:
• |z
1
+ z
2
| ≤ |z
1
| + |z
2
|, dấu "=" khi z
1
= kz
2
với k ≥ 0.
• |z
1
− z
2
| ≤ |z
1
| + |z
2
|, dấu "=" khi z
1
= kz
2
với k ≤ 0.
• |z
1
+ z
2
| ≥ ||z
1
| − |z
2
||, dấu "=" khi z
1
= kz
2
với k ≤ 0.
• |z
1
− z
2
| ≥ ||z
1
| − |z
2
||, dấu "=" khi z
1
= kz
2
với k ≥ 0.
2. Công thức trung tuyến: |z
1
+ z
2
|
2
+ |z
1
− z
2
|
2
= 2(|z
1
|
2
+ |z
2
|
2
)
3. Tập hợp điểm:
• |z −(a + bi)| = r : Đường tròn tâm I(a; b) bán kính r.
• |z −(a
1
+ b
1
i)| = |z − (a
2
+ b
2
i)|: Đường trung trực của AB với A(a
1
; b
1
), B(a
2
; b
2
).
• |z −(a
1
+ b
1
i)| + |z −(a
2
+ b
2
i)| = 2a:
– Đoạn thẳng AB với A(a
1
; b
1
), B(a
2
; b
2
) nếu 2a = AB.
– Elip (E) nhận A, B làm hai tiêu điểm với độ dài trục lớn là 2a nếu 2a > AB.
Đặc biệt |z + c|+ |z − c| = 2a: Elip (E) :
x
2
a
2
+
y
2
b
2
= 1 với b =
√
a
2
− c
2
.
B. CÁC DẠNG BÀI TẬP
Phương pháp đại số
VÍ DỤ 1 (Sở GD Hưng Yên 2017). Cho số phức z thỏa mãn |z −1 −2i| = 4. Gọi M, m lần
lượt là giá trị lớn nhất, giá trị nhỏ nhất của |z + 2 + i|. Tính S = M
2
+ m
2
.
A. S = 34 B. S = 82 C. S = 68 D. S = 36
LỜI GIẢI 1. Ta có
4 = |z + 2+ i −(3+ 3i)| ≥ ||z + 2 + i|−|3 + 3i|| = ||z + 2 + i|−3
√
2| ⇒
(
|z + 2 + i| ≤ 4 + 3
√
2 = M
|z + 2 + i| ≥ 3
√
2 − 4 = m
.
Khi đó S = M
2
+ m
2
= 68.
Đáp án là C.
VÍ DỤ 2 (Sở GD Hà Tĩnh 2017). Trong các số phức z thỏa mãn |z − (2 + 4i)| = 2, gọi z
1
và z
2
là số phức có mô đun lớn nhất và nhỏ nhất. Tổng phần ảo của hai số phức z
1
và z
2
bằng
A. 8i B. 4 C. −8 D. 8
1
https://www.facebook.com/luong.d.trong
LỜI GIẢI. Ta có
2 ≥ ||z| − |2 + 4i|| = ||z| − 2
√
5| ⇒ 2
√
5 − 2 ≤ |z| ≤ 2
√
5 + 2.
Giá trị lớn nhất |z| là 2
√
5 − 2 khi z = k(2 + 4i) với (k − 1)
√
5 = 1 ⇒ k = 1 +
1
√
5
. Do đó
z
1
=
1 +
1
√
5
(2 + 4i).
Giá trị nhỏ nhất |z| là 2
√
5 − 2 khi z = k(2 + 4i) với (1 − k)
√
5 = 1 ⇒ k = 1 −
1
√
5
. Do đó
z
2
=
1 −
1
√
5
(2 + 4i).
Như vậy, tổng hai phần ảo của z
1
, z
2
là 4
1 +
1
√
5
+ 4
1 −
1
√
5
= 8.
Đáp án là D.
VÍ DỤ 3 (THPT Chuyên Thái Nguyên 2017 L3). Cho số phức z thỏa mãn |z
2
+ 4| = 2|z|.
Kí hiệu M = max |z|, m = min |z|. Tìm mô đun của số phức w = M + mi.
A. |w| = 2
√
3 B. |w| =
√
3 C. |w| = 2
√
5 D. |w| =
√
5
LỜI GIẢI. Ta có
2|z| ≥ |z|
2
− 4 ⇔ |z|
2
− 2|z| − 4 ≤ 0 ⇒ |z| ≤ 1 +
√
5 = M.
và
2|z| ≥ 4 − |z|
2
⇔ |z|
2
+ 2|z| − 4 ≥ 0 ⇒ |z| ≥ −1 +
√
5 = m.
Vậy |w| =
√
M
2
+ m
2
= 2
√
3.
Đáp án là A.
VÍ DỤ 4 (THPT Yên Lạc-Vĩnh Phúc 2017). Trong các số phức z thỏa mãn |2z +z| = |z −i|,
tìm số phức có phần thực không âm sao cho |z
−1
| đạt giá trị lớn nhất.
A. z =
√
6
4
+
i
2
B. z =
i
2
C. z =
√
3
4
+
i
8
D. z =
√
6
8
+
i
8
LỜI GIẢI. Gọi z = a + bi (a ≥ 0) thì z = a − bi. Khi đó
√
9a
2
+ b
2
=
p
a
2
+ (b − 1)
2
⇔ 2b = 1 − 8a
2
⇔ b =
1
2
− 4a
2
.
Ta có |z
−1
| =
1
|z|
lớn nhất khi và chỉ khi |z| =
√
a
2
+ b
2
nhỏ nhất.
|z|
2
= a
2
+
1
2
− 4a
2
2
= 16a
4
− 3a
2
+
1
4
=
4a
2
−
3
8
2
+
7
64
≥
7
64
⇒ |z| ≥
√
7
8
.
Do đó số phức z cần tìm thỏa mãn
a
2
=
3
32
⇒ a =
√
6
8
b =
1
2
− 4a
2
=
1
8
. Vậy z =
√
6
8
+
i
8
.
Đáp án là D.
2
Lương Đức Trọng - ĐHSPHN (SĐT:0982715678)
Phương pháp hình học
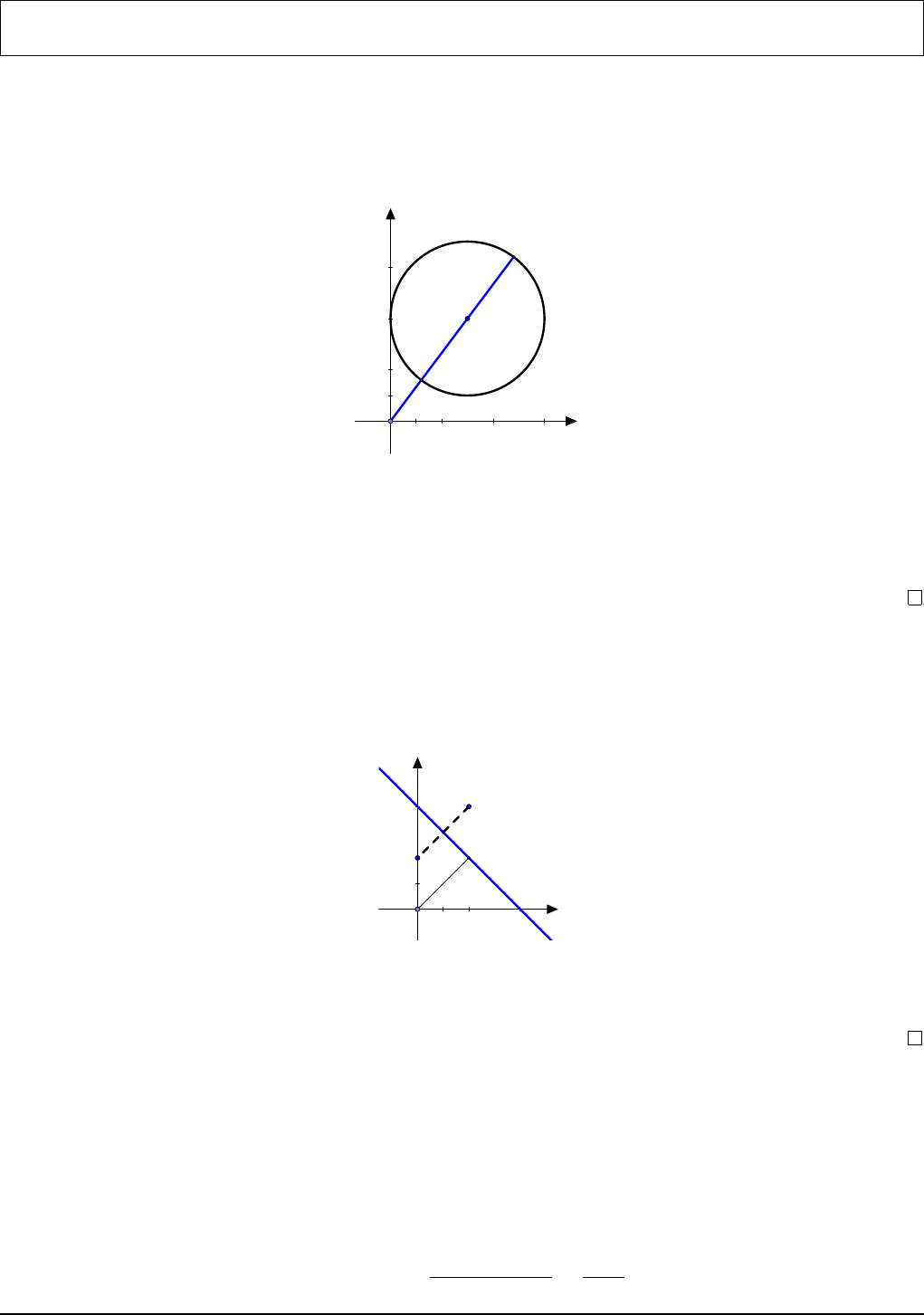
VÍ DỤ 5 (THPT Phan Bội Châu-Đăk Lăk 2017). Cho số phức z thỏa mãn |z −3−4i| = 1.
Mô đun lớn nhất của số phức z là:
A. 7 B. 6 C. 5 D. 4
LỜI GIẢI.
x
y
I
O
M
N
Tập hợp các điểm M biểu diễn số phức z thỏa mãn giả thiết là đường tròn tâm I(3; 4) bán
kính r = 3. Khi đó |z| = OM với O là gốc tọa độ. Do đó
max |z| = OI + r = 5 + 1 = 6.
Đáp án là B.
VÍ DỤ 6 (THPT Đồng Quan-Hà Nội 2017,THPT Chuyên Biên Hòa-Hà Nam 2017).
Trong các số phức z thỏa mãn |z − 2 − 4i| = |z − 2i|. Tìm số phức z có mô đun nhỏ nhất
A. z = 2 − 2i B. z = 1 + i C. z = 2 + 2i D. z = 1 − i
LỜI GIẢI.
x
y
A
B
I
K
O
H
Gọi A(2; 4), B(0; 2), tập hợp các điểm z thỏa mãn giả thiết đề bài là đường trung trực d
của AB có phương trình x + y −4 = 0. Khi đó |z| = OM nhỏ nhất khi M là hình chiếu của
O trên d là H(2; 2).
Đáp án là C.
VÍ DỤ 7 (THPT Trần Phú-Hà Nội 2017). Cho số phức z thỏa mãn |z + 3| + |z − 3| = 10.
Giá trị nhỏ nhất của |z| là
A. 3 B. 4 C. 5 D. 6
LỜI GIẢI. Gọi A(−3; 0), B(3; 0) có trung điểm là O(0; 0). Điểm M biểu diễn số phức z. Theo
công thức trung tuyến thì
|z|
2
= MO
2
=
MA
2
+ MB
2
2
−
AB
2
4
.
3
Chia sẻ bởi: 
Trịnh Thị Thanh
Trịnh Thị Thanh Liên kết tải về
Link Download chính thức:
Hướng dẫn giải bài toán cực trị số phức 242,8 KB 22/03/2019 Download
Có thể bạn quan tâm
-
Cách thay thế từ/cụm từ trong bài nghị luận văn học
-
Tập làm văn lớp 5: Tả cảnh buổi sáng trên cánh đồng
-
Tổng hợp dàn ý bài Câu cá mùa thu (9 Mẫu)
-
Soạn bài Tục ngữ về thiên nhiên, lao động và con người, xã hội (2) - Cánh diều 7
-
Cảm nhận về bài thơ Câu cá mùa thu của Nguyễn Khuyến
-
Mẫu vở tập tô chữ cho bé - Tập tô chữ cái cho bé chuẩn bị vào lớp 1
-
Phân tích bài thơ Câu cá mùa thu của Nguyễn Khuyến (3 Dàn ý + 19 mẫu)
-
Văn mẫu lớp 9: Nghị luận về vai trò của lao động đối với con người
-
Văn mẫu lớp 10: Dàn ý phân tích bài thơ Nắng mới (5 mẫu)
-
Văn mẫu lớp 10: Cảm nhận bài thơ Nắng mới (Dàn ý + 6 Mẫu)
Sắp xếp theo
