Đề thi Olympic môn Toán lớp 9 - Phòng GD Đức Thọ tỉnh Hà Tĩnh Năm học 2012 - 2013

Tải về Bình luận

PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỨC THỌ

ĐỀ THI CHÍNH THỨC

ĐỀ THI OLYMPIC TOÁN LỚP 9
NĂM HỌC 2012 - 2013

Thời gian làm bài: 120 phút (không kể thời gian giao đề)

Bài 1:

a. Giải phương trình:

b. Với giá trị nào của tham số a thì phương trình sau có nghiệm:

Bài 2:

a. Tìm GTNN của biểu thức:

b. Tìm số thực a để phương trình sau có nghiệm nguyên: x² - ax + a + 2 = 0

Bài 3:

a. Chứng minh rằng đường thẳng (d) có phương trình (m - 3)x - (m - 2)y + m - 1 = 0 (m là tham số) luôn đi qua một điểm cố định A. Tìm tọa độ A

b. Giải hệ phương trình sau: 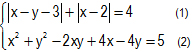Đề thi Olympic môn Toán lớp 9 - Phòng GD Đức Thọ tỉnh Hà Tĩnh

Bài 4:

Cho ΔABC đều cố định nội tiếp trong đường tròn (O). Đường thẳng d thay đổi luôn đi qua A và cắt cung nhỏ AB tại điểm E (E # A). Đường thẳng d cắt hai tiếp tuyên tại B và C của đường tròn (O) lần lượt tại M và N, MC cắt BN tại F. Chứng minh rằng:

a. ΔCAN ~ ΔBMA và ΔMBC ~ ΔBCN

b. Tứ giác BMEF nội tiếp được đường tròn

c. Chứng minh rằng đường thẳng EF luôn đi qua một điểm cố định khi d thay đổi

Bài 5:

Cho a, b, c > 0. Chứng minh rằng:

Download tài liệu để xem thêm chi tiết.

Chia sẻ bởi:

Tải về

Liên kết tải về

Đề thi Olympic môn Toán lớp 9 - Phòng GD Đức Thọ tỉnh Hà Tĩnh 227 KB Tải về

Tìm thêm: Toán 9

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!