Đề thi Olympic môn Toán lớp 8 - Phòng GD Đức Thọ tỉnh Hà Tĩnh Năm học 2012 - 2013

Tải về Bình luận

3

PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỨC THỌ

ĐỀ THI CHÍNH THỨC

ĐỀ THI OLYMPIC TOÁN LỚP 8
NĂM HỌC 2012 - 2013

Thời gian làm bài: 120 phút (không kể thời gian giao đề)

Câu 1:

Cho biểu thức: 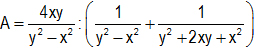Đề thi Olympic môn Toán lớp 8

a. Tìm điều kiện x, y để giá trị của A được xác định

b. Rút gọn A

c. Nếu x, y là các số thực thỏa mãn: 3x² + y² + 2x - 2y = 1, hãy tìm các giá trị nguyên dương của A?

Câu 2:

a. Giải phương trình sau:

b. Tìm các số x, y, z biết x² + y² + z² = xy = yz + zx và x²⁰¹² + y²⁰¹² + z²⁰¹² = 3²⁰¹³

Câu 3:

a. Cho phương trình , với m là tham số. Tìm m để phương trình có nghiệm dương

b. Chứng minh rằng nếu a + b + c ≥ 3 thì a³ + b³ + c³ ≤ a⁴ + b⁴ + c⁴

Câu 4:

Cho đoạn thẳng AB, gọi O là trung điểm của AB. Vẽ về một phía của AB các tia Ax, By vuông góc với điểm C trên tia Ax, điểm D trên tia by sao cho góc COD = 90^o

a. Chứng minh rằng ΔACO ~ ΔBOD và ΔOCD ~ ΔBOD

b. Kẻ OI vuông góc (I thuộc CD), gọi K là giao điểm của AD và BC. Chứng minh rằng IK // AC.

c Gọi E là giao ddierm của OD với IK. Chứng minh rằng IE = BD

Câu 5:

Cho

So sánh S với

Download tài liệu để xem thêm chi tiết.

Chia sẻ bởi:

Tải về

Liên kết tải về

Đề thi Olympic môn Toán lớp 8 - Phòng GD Đức Thọ tỉnh Hà Tĩnh 243 KB Tải về

Tìm thêm: Toán lớp 8 Toán 8

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!

Sắp xếp theo

Tài liệu tham khảo khác

Chủ đề liên quan

Có thể bạn quan tâm

Xem thêm

Mới nhất trong tuần

Đóng

Chỉ thành viên Download Pro tải được nội dung này! Download Pro - Tải nhanh, website không quảng cáo! Tìm hiểu thêm

Mua Download Pro 79.000đ