Cách chứng minh nhiều điểm cùng thuộc một đường tròn Ôn tập Toán 9
Chứng minh nhiều điểm cùng thuộc một đường tròn là tài liệu vô cùng hữu ích tổng hợp kiến thức lý thuyết, các cách chứng minh, ví dụ minh họa có đáp án giải chi tiết.
Cách chứng minh nhiều điểm cùng thuộc một đường tròn là một trong những bài toán cơ bản trong chương trình lớp 9 thường xuất hiện trong các bài thi vào 10. Qua đó giúp các bạn học sinh tham khảo, hệ thống lại kiến thức để giải nhanh các bài tập hình học về chứng minh nhiều điểm thuộc một đường tròn. Ngoài ra để nâng cao kiến thức môn Toán thật tốt các bạn xem thêm một số tài liệu như: cách tính bán kính đường tròn ngoại tiếp tam giác, tâm đường tròn ngoại tiếp tam giác.
Chứng minh nhiều điểm cùng thuộc một đường tròn
1. Đường tròn là gì?
- Đường tròn tâm O bán kính R > 0 là hình gồm các điểm cách đều O một khoảng R kí hiệu là (O; R) hay (O)
+ Đường tròn đi qua các điểm A1, A2, …, An gọi là đường tròn ngoại tiếp đa giác A1A2…An
+ Đường tròn tiếp xúc với tất cả các cạnh của đa giác được gọi là đường tròn nội tiếp đa giác đó.
2. Cách chứng minh nhiều điểm cùng thuộc một đường tròn
Cách 1: Chứng minh các điểm cùng cách đều một điểm O một khoảng bằng R. Khi đó các điểm đó sẽ thuộc đường tròn tâm O, bán kính R.
Cách 2: Sử dụng cung chứa góc: Chứng minh các điểm liên tiếp cùng nhìn một đoạn AB cố định dưới một góc α bằng nhau. Hay chính là các điểm đó cùng thuộc một cung chứa góc α dựng trên đoạn AB, nên các điểm đó cùng thuộc một đường tròn chứa cung chứa góc α dựng trên đoạn AB.
3. Cách chứng minh 5 điểm cùng thuộc một đường tròn
* Cách 1: Chứng minh 5 điểm (các điểm) đó cùng cách đều một điểm O cố định. Khi đó các điểm đã cho cùng thuộc đường tròn tâm O.
* Cách 2: Sử dụng tứ giác nội tiếp. Chẳng hạn để chứng minh 5 điểm A, B, C, D, E cùng thuộc một đường tròn ta chứng minh ABCD, ABCE là tứ giác nội tiếp cùng 1 đường tròn tâm O.
* Ví dụ 4: Cho tam giác ABC vuông tại A. Trên AC lấy điểm D. Hình chiếu của D lên BC là E, điểm đối xứng của E qua BD là F. Chứng minh 5 điểm A, B, E, D, F cùng nằm trên một đường tròn. Xác định tâm O của đường tròn đó.
* Lời giải:
- Ta có hình vẽ như sau:
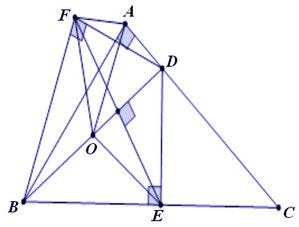
- Theo giả thuyết, DE ⊥ BC nên ∠BEB = 900
- Vì E và F đối xứng với nhau qua BD nên BD là đường trung trực của đoạn thẳng EF nên suy ra:
BF = BE và DF = DE
Suy ra: ΔBFD = ΔBED (c-c-c)
Suy ra: ∠BFD = ∠BEB = 900
- Gọi O là trung điểm của BD.
- Xét tam giác vuông ABD vuông tại A có AO là trung tuyến nên:
AO = ½BD = OB = OD (1)
- Xét tam giác vuông BDE vuông tại E có OE là trung tuyến nên:
EO = ½BD = OB = OD (2)
- Xét tam giác vuông BFD vuông tại F có OF là trung tuyến nên:
FO = ½BD = OB = OD (3)
Từ (1), (2) và (3) suy ra: OA = OB = OD = OE = OF.
Vậy 5 điểm A, B, E, D, F cùng nằm trên một đường tròn tâm O với O là trung điểm của BC.
4. Tính chất đối xứng của đường tròn
a) Tâm đối xứng
Đường tròn là hình có tâm đối xứng. Tâm của đường tròn là tâm đối xứng của đường tròn đó.
b) Trục đối xứng
Đường tròn là hình có trục đối xứng. Bất kì đường kính nào cũng là trục đối xứng của đường tròn
5. Ví dụ chứng minh các điểm nằm trên đường tròn
Ví dụ 1: Cho I, O lần lượt là tâm đường tròn nội tiếp, tâm đường tròn ngoại tiếp tam giác ABC với A = 60o. Gọi H là giao điểm của các đường cao BB' và CC'. Chứng minh các điểm B, C, O, H, I cùng thuộc một đường tròn.
Hướng dẫn giải
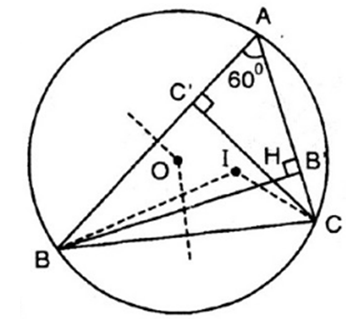
![]() \(\widehat{BOC}\) là góc ở tâm chắn cung BC
\(\widehat{BOC}\) là góc ở tâm chắn cung BC
![]() \(\widehat{BAC}\) là góc nội tiếp chắn cung BC
\(\widehat{BAC}\) là góc nội tiếp chắn cung BC
⇒![]() \(\widehat{BOC}\) = 2
\(\widehat{BOC}\) = 2![]() \(\widehat{BAC}\) = 2.600 = 1200 (1)
\(\widehat{BAC}\) = 2.600 = 1200 (1)
+ Tứ giác AC’HB’ có:
![]() \(\widehat{A} + \widehat{AB'H} + \widehat{AC'H} + \widehat{B'HC'}\)= 3600
\(\widehat{A} + \widehat{AB'H} + \widehat{AC'H} + \widehat{B'HC'}\)= 3600
Mà ![]() \(\widehat{A}\) = 600 ,
\(\widehat{A}\) = 600 , ![]() \(\widehat{AB'H}\)=
\(\widehat{AB'H}\)= ![]() \(\widehat{AC'H}\) = 90o ( BB’, CC’ là các đường cao)
\(\widehat{AC'H}\) = 90o ( BB’, CC’ là các đường cao)
![]() \(\widehat{B'HC'}\) = 3600- (600 +900 + 900) = 1200
\(\widehat{B'HC'}\) = 3600- (600 +900 + 900) = 1200
![]() \(\widehat{B'HC} = \widehat{B'HC'}\)= = 1200 (2)
\(\widehat{B'HC} = \widehat{B'HC'}\)= = 1200 (2)
+ Do I là tâm đường tròn nội tiếp tam giác ABC
Suy ra BI, CI lần lượt là các tia phân giác của ![]() \(\widehat{ABC} = \widehat{ACB}\)
\(\widehat{ABC} = \widehat{ACB}\)
![]() \(⇒\widehat{IBC} = 1/2\widehat{ABC}\)
\(⇒\widehat{IBC} = 1/2\widehat{ABC}\)
![]() \(⇒\widehat{ICB}\) =
\(⇒\widehat{ICB}\) = ![]() \(\frac{1}{2}\)
\(\frac{1}{2}\)![]() \(\widehat{ACB}\)
\(\widehat{ACB}\)
Xét tam giác IBC, ta có: ![]() \(\widehat{BIC} = 180 - (\widehat{IBC} + \widehat{ICB})\)
\(\widehat{BIC} = 180 - (\widehat{IBC} + \widehat{ICB})\)
1800- 600 = 1200 (3)
Từ (1), (2) và (3)
![]() \(\widehat{BHC} = \widehat{BIC} =\widehat{BOC} =\)1200
\(\widehat{BHC} = \widehat{BIC} =\widehat{BOC} =\)1200
Do đó, H, I và O cùng nhìn BC cố định dưới một góc 120o.
Suy ra, H, I và O thuộc cung chứa góc 120o dựng trên đoạn BC.
⇒ B, O, I, H, C cùng thuộc đường tròn chứa cung 120o dựng trên đoạn BC.
Ví dụ 2 : Cho nửa đường tròn đường kính AB trên đó lấy hai điểm D và E ( E nằm giữa A và D). AD cắt BE tại I, AE cắt BD tại F.
a. Chứng minh IF ⊥ AB tại J
b. Gọi P, Q, R lần lượt là trung điểm của AB, AF, IF. Chứng minh 4 điểm J, P, Q, R cùng nằm trên một đường tròn.
Hướng dẫn giải
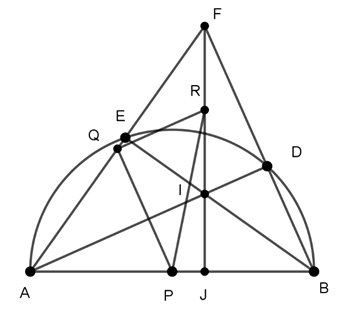
a. Ta có D, E thuộc đường tròn đường kính AB
![]() \(\widehat{ADB}\) = 900
\(\widehat{ADB}\) = 900 ![]() \(\widehat{RJP}\)= 900(góc nội tiếp chắn nửa đường tròn)
\(\widehat{RJP}\)= 900(góc nội tiếp chắn nửa đường tròn)
⇒ AD, BE là đường cao của tam giác AFB
Mà BE giao AD tại I
⇒ I là trực tâm của tam giác AFB
⇒ IF là đường cao của tam giác AFB
⇒ IF ⊥ AB tại J (đpcm)
b. ΔPJR vuông tại J (IJ ⊥ AB) ⇒ ![]() \(\widehat{RJP}\)= 900⇒ J nằm trên đường tròn đường kính PR (*)
\(\widehat{RJP}\)= 900⇒ J nằm trên đường tròn đường kính PR (*)
P, Q là trung điểm của AB và BF ⇒ PQ là đường trung bình của ΔABF
⇒ PQ // BF
Mà AD BF
⇒ AD ⊥ PQ
R, Q là trung điểm IF và BF ⇒ RQ là đường trung bình của ΔIFA
⇒ RQ // AD
Mà AD ⊥ PQ
⇒ RQ ⊥ PQ
⇒ ![]() \(\widehat{RQP}\) = 900
\(\widehat{RQP}\) = 900
⇒ Q nằm trên đường tròn đường kính PR (**)
Từ (*) và (**) suy ra bốn điểm P, Q, R, J cùng nằm trên đường tròn đường kính PR.
Ví dụ 3 Cho tam giác ABC cân tại A nội tiếp đường tròn (O). Gọi M là trung điểm của AC, G là trọng tâm của tam giác ABM. Gọi Q là giao điểm của BM và GO. Xác định tâm đường tròn ngoại tiếp tam giác BGQ
Gợi ý đáp án
Vì tam giác ABC cân tại A nên tâm O của đường tròn ngoại tiếp tam giác nằm trên đường trung trực của BC.
Gọi K là giao điểm của AO và BM
Dựng các đường trung tuyến MN và BP của tam giác ABM cắt nhau tại trọng tâm G
Do MN // BC
=> MN ⊥ AO
Do K là giao của AO và NM
=> K là trọng tâm tam giác ABC
=> GK // AC
Mặt khác ta có OM ⊥ AC
=> GK ⊥ OM
=> K là trực tâm của tam giác OMG
=> MK ⊥ OG
Như vậy tam giác BGQ vuông tại Q
=> Tâm đường tròn ngoại tiếp tam giác GBQ là trung điểm I của BG
Ví dụ 4: Cho hình vuông ABCD. Gọi M là trung điểm của BC, N là điểm thuộc đường chéo CA sao cho AN = AC/4. Chứng minh 4 điểm M, N, C, D nằm trên cùng một đường tròn.
Gợi ý đáp án
Ta có tứ giác MNCD có góc MCD = 900
=> Để chứng minh 4 điểm M, N, C, D cùng nằm trên một đường tròn ta sẽ chứng minh góc MND = 900
Cách 1: Qua N kẻ đường thẳng song song với AB cắt BC và AD lần lượt tại E và F
Xét hai tam giác vuông NEM và DFN cps
EM = NF = AB/4
EN = DF = AB /4
=> ∆NEM = ∆DFN
![]() \(\Rightarrow \widehat {NME} = \widehat {DFN},\widehat {MNE} = \widehat {NDF} \Rightarrow \widehat {MNE} + \widehat {DNF} = {90^0}\)
\(\Rightarrow \widehat {NME} = \widehat {DFN},\widehat {MNE} = \widehat {NDF} \Rightarrow \widehat {MNE} + \widehat {DNF} = {90^0}\)
Hay tam giác MND vuông tại N
=> 4 điểm M, N, C, D cùng nằm trên đường tròn đường kinh MD
Cách 2: Gọi K là trung điểm của DI với I là giao điểm của hai đường chéo
Dễ thấy MCKN là hình bình hành
=> MN // CK
Mặt khác do NK ⊥ CD, DK ⊥ CN => K là trực tâm của tam giác CDN
=> CK ⊥ ND => MN ⊥ ND
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:












 Đề thi giữa kì 2 lớp 9
Đề thi giữa kì 2 lớp 9
 Đề thi học kì 2 Lớp 9
Đề thi học kì 2 Lớp 9
 Đề thi giữa kì 1 lớp 9
Đề thi giữa kì 1 lớp 9
 Đề thi học kì 1 Lớp 9
Đề thi học kì 1 Lớp 9
 Toán 9
Toán 9
 Toán 9 Kết nối tri thức
Toán 9 Kết nối tri thức
 Toán 9 Cánh Diều
Toán 9 Cánh Diều
 Toán 9 Chân trời sáng tạo
Toán 9 Chân trời sáng tạo
 Văn 9 Kết nối tri thức
Văn 9 Kết nối tri thức









