Chuyên đề phương trình đại số Chuyên đề phương trình, bất phương trình và hệ phương trình đại số
Nhằm đem đến cho các bạn có thêm nhiều tài liệu học tập Eballsviet.com xin giới thiệu tài liệu Chuyên đề phương trình đại số lớp 10.
Đây là tài liệu cực kì hữu ích, gồm 23 trang trình bày đầy đủ các dạng toán phương trình, bất phương trình và hệ phương trình với các bài toán được giải chi tiết. Hy vọng với tài liệu này các bạn học sinh lớp 10 có thêm nhiều tài liệu tham khảo, củng cố kiến thức để đạt được điểm cao trong các bài thi học kì 1, kì 2. Mời các bạn cùng tham khảo và tải tài liệu tại đây.
Chuyên đề phương trình đại số
GV.Lưu Huy Thưởng 0968.393.899
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 1
CHUYÊN ĐỀ PHƯƠNG TRÌNH VÀ BẤT PHƯƠNG TRÌNH
BÀI 1: ĐẠI CƯƠNG VỀ PHƯƠNG TRÌNH VÀ BẤT PHƯƠNG TRÌNH
I. KIẾN THỨC CẦN NHỚ
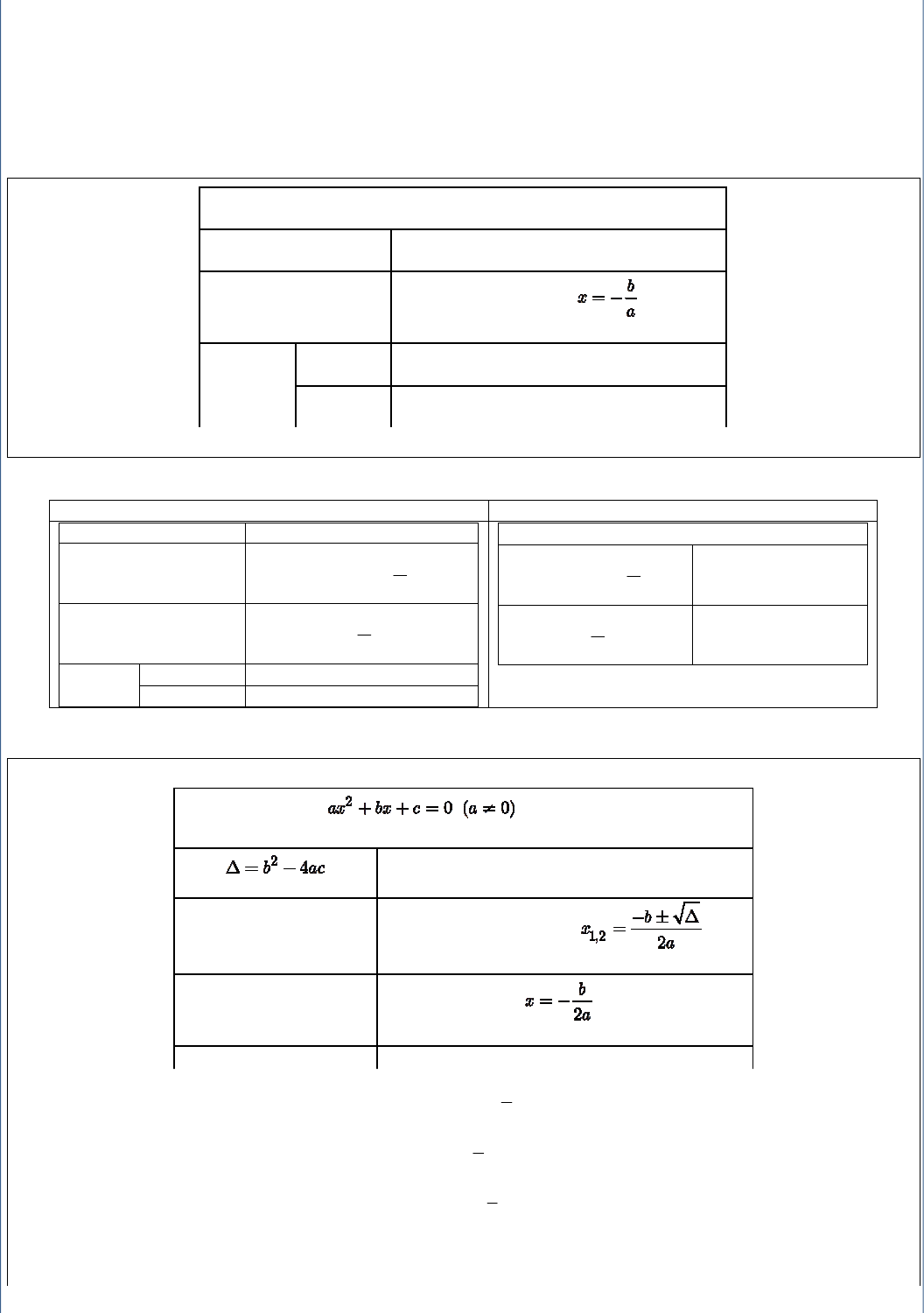
1. PHƯƠNG TRÌNH DẠNG:
0
ax b
+ =
Chú ý: Khi a
≠
0 thì (1) được gọi là phương trình bậc nhất một ẩn.
2. BẤT PHƯƠNG TRÌNH DẠNG
0
ax b
+ <
Biện luận Dấu nhị thức bậc nhất
Điều kiện Kết quả tập nghiệm
a > 0
S =
b
a
;
−∞ −
a < 0
S =
b
a
;
− +∞
a = 0
b
≥
0 S =
∅
b < 0 S = R
f(x) = ax + b (a
≠
0)
x
∈
b
a
;
−∞ −
a.f(x) < 0
x
∈
b
a
;
− +∞
a.f(x) > 0
3. PHƯƠNG TRÌNH BẬC HAI:
2
0
ax bx c
+ + =
1. Cách giải
Chú ý: – Nếu a + b + c = 0 thì (1) có hai nghiệm là x = 1 và x =
c
a
.
– Nếu a – b + c = 0 thì (1) có hai nghiệm là x = –1 và x =
c
a
−
.
– Nếu b chẵn thì ta có thể dùng công thức thu gọn với
2
b
b
′
=
.
2. Định lí Vi–et
Hai số
1 2
,
x x
là các nghiệm của phương trình bậc hai
2
0
ax bx c
+ + =
khi và chỉ khi chúng thoả mãn các hệ thức
ax + b = 0 (1)
Hệ số Kết luận
a
≠
0
(1) có nghiệm duy nhất
a = 0
b
≠
0
(1) vô nghiệm
b = 0 (1) nghiệm đúng với mọi x
(1)
Kết luận
∆
> 0
(1) có 2 nghiệm phân biệt
∆
= 0
(1) có nghiệm kép
∆
< 0
(1) vô nghiệm
GV.Lưu Huy Thưởng 0968.393.899
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 2
1 2
b
S x x
a
= + = −
và
1 2
c
P x x
a
= =
.
4. BẤT PHƯƠNG TRÌNH BẬC HAI
Xét dấu tam thức bậc hai Giải bất phương trình bậc hai
f(x) =
2
ax bx c
+ +
(a
≠
≠≠
≠
0)
∆
< 0 a.f(x) > 0,
∀
x
∈
R
∆
= 0
a.f(x) > 0,
∀
x
∈
\
2
b
R
a
−
∆
> 0
a.f(x) > 0,
∀
x
∈
(–∞; x
1
)
∪
(x
2
;
+∞)
a.f(x) < 0,
∀
x
∈
(x
1
; x
2
)
Dựa vào định lý dấu tam thức bậc hai để giải
II. CÁC DẠNG TOÁN
1. Dạng toán 1: Giải và biện luận phương trình và bất phương trình
HT1. Giải và biện luận các phương trình sau theo tham số m:
1)
2
( 2) 2 3
m x m x
+ − = −
2)
( ) 2
m x m x m
− = + −
3)
( 3) ( 2) 6
m x m m x
− + = − +
4)
2
( 1) (3 2)
m x m x m
− + = −
5)
2 2
( ) 2 1
m m x x m
− = + −
6)
2
( 1) (2 5) 2
m x m x m
+ = + + +
HT2. Giải các bất phương trình sau:
1)
(2 5)( 2)
0
4 3
x x
x
− +
>
− +
2)
3 5
1 2
x x
x x
− +
>
+ −
3)
3 1 2
5 3
x x
x x
− −
<
+ −
4)
3 4
1
2
x
x
−
>
−
5)
2 5
1
2
x
x
−
≥ −
−
6)
2 5
1 2 1
x x
≤
− −
HT3. Giải và biện luận các bất phương trình sau:
1)
( ) 1
m x m x
− ≤ −
2)
6 2 3
mx x m
+ > +
3)
( 1) 3 4
m x m m
+ + < +
4)
2
1
mx m x
+ > +
5)
( 2)
1
6 3 2
m x
x m x
−
− +
+ >
6)
2
3 2( ) ( 1)
mx x m m
− < − − +
HT4. Giải và biện luận các bất phương trình sau:
1)
2 1
0
1
x m
x
+ −
>
+
2)
1
0
1
mx m
x
− +
<
−
3)
1( 2) 0
x x m
− − + >
HT5. Giải và biện luận các phương trình sau:
1)
2
5 3 1 0
x x m
+ + − =
2)
2
2 12 15 0
x x m
+ − =
3)
2 2
2( 1) 0
x m x m
− − + =
4)
2
( 1) 2( 1) 2 0
m x m x m
+ − − + − =
5)
2
( 1) (2 ) 1 0
m x m x
− + − − =
6)
2
2( 3) 1 0
mx m x m
− + + + =
HT6. Giải và biện luận các bất phương trình sau:
1)
2
3 0
x mx m
− + + >
2)
2
(1 ) 2 2 0
m x mx m
+ − + ≤
3)
2
2 4 0
mx x
− + >
HT7. Trong các phương trình sau, tìm giá trị của tham số để phương trình:
i) Có nghiệm duy nhất ii) Vô nghiệm iii) Nghiệm đúng với mọi x ∈ R.
GV.Lưu Huy Thưởng 0968.393.899
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 3
1)
( 2) 1
m x n
− = −
2)
2
( 2 3) 1
m m x m
+ − = −
3)
2
( 2)( 1) ( )
mx x mx m x
+ + = +
4)
2 2
( ) 2 1
m m x x m
− = + −
HT8. Tìm m để các bất phương trình sau vô nghiệm:
a)
2 2
4 3
m x m x m
+ − < +
b)
2
1 (3 2)
m x m m x
+ ≥ + −
c)
2
4
mx m mx
− > −
d)
2
3 2( ) ( 1)
mx x m m
− < − − +
2. Dạng toán 2: Dấu của nghiệm số phương trình bậc hai
2
0 ( 0) (1)
ax bx c a+ + = ≠
•
(1) có hai nghiệm trái dấu
⇔
P < 0
•
(1) có hai nghiệm cùng dấu
⇔
0
0
P
∆ ≥
>
•
(1) có hai nghiệm dương
⇔
0
0
0
P
S
∆ ≥
>
>
•
(1) có hai nghiệm âm
⇔
0
0
0
P
S
∆ ≥
>
<
Chú ý: Trong các trường hợp trên nếu yêu cầu hai nghiệm phân biệt thì
∆
> 0.
Bài tập
HT9. Xác định m để phương trình:
i) có hai nghiệm trái dấu ii) có hai nghiệm âm phân biệt
iii) có hai nghiệm dương phân biệt
1)
2
5 3 1 0
x x m
+ + − =
2)
2
2 12 15 0
x x m
+ − =
3)
2 2
2( 1) 0
x m x m
− − + =
4)
2
( 1) 2( 1) 2 0
m x m x m
+ − − + − =
5)
2
( 1) (2 ) 1 0
m x m x
− + − − =
6)
2
2( 3) 1 0
mx m x m
− + + + =
7)
2
4 1 0
x x m
− + + =
8)
2
( 1) 2( 4) 1 0
m x m x m
+ + + + + =
3. Dạng toán 3: Áp dụng định lý Viet
a. Biểu thức đối xứng của các nghiệm số
Ta sử dụng công thức
1 2 1 2
;
b c
S x x P x x
a a
= + = − = =
để biểu diễn các biểu thức đối xứng của các nghiệm x
1
, x
2
theo S và P.
Ví dụ:
2 2 2 2
1 2 1 2 1 2
( ) 2 2
x x x x x x S P
+ = + − = −
3 3 2 2
1 2 1 2 1 2 1 2
( ) ( ) 3 ( 3 )
x x x x x x x x S S P
+ = + + − = −
b. Hệ thức của các nghiệm độc lập đối với tham số
Để tìm hệ thức của các nghiệm độc lập đối với tham số ta tìm:
1 2 1 2
;
b c
S x x P x x
a a
= + = − = =
(S, P có chứa tham số m).
Khử tham số m giữa S và P ta tìm được hệ thức giữa x
1
và x
2
.
c. Lập phương trình bậc hai
Nếu phương trình bậc hai có các nghiệm u và v thì phương trình bậc hai có dạng:
2
0
x Sx P
− + =
, trong đó S = u + v, P = uv.
Bài tập
HT10. Gọi
1 2
,
x x
là các nghiệm của phương trình. Không giải phương trình, hãy tính:
Chia sẻ bởi: 
Trịnh Thị Thanh
Trịnh Thị Thanh Liên kết tải về
Chuyên đề phương trình đại số 761,5 KB Tải về
Có thể bạn quan tâm
-
Phân biệt phản xạ có điều kiện và phản xạ không điều kiện
-
Bộ đề thi giữa học kì 2 lớp 7 năm 2023 - 2024 (Sách mới)
-
Thuyết minh về cách làm một món ăn mà em yêu thích (Dàn ý + 18 mẫu)
-
Đoạn văn tiếng Anh viết về hệ thống giáo dục ở Việt Nam (Dàn ý + 10 Mẫu)
-
Tập làm văn lớp 4: Tả cây cam mà em yêu thích
-
Mẫu kế hoạch công tác chủ nhiệm năm học 2024 - 2025 (Cách viết + 12 Mẫu)
-
Hợp đồng mua bán máy móc, thiết bị
-
Viết đoạn văn tiếng Anh về nguyên nhân khiến các bạn căng thẳng
-
Nghị luận về sức mạnh của niềm tin (Dàn ý + 32 mẫu)
-
Soạn bài Đừng gây tổn thương - Cánh diều 10
Xác thực tài khoản!
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:
Số điện thoại chưa đúng định dạng!
Sắp xếp theo
