Eballsviet.com Học tập Lớp 11 Toán 11

Chuyên đề phép dời hình và phép đồng dạng trong mặt phẳng Tài liệu ôn tập Hình học lớp 11 chương 1

Giới thiệu Tải về Bình luận
  • 5

Với mong muốn đem đến cho các bạn học sinh lớp 11 có thêm nhiều tài liệu ôn tập Toán phần Hình học, Eballsviet.com xin giới thiệu tài liệu Chuyên đề phép dời hình và phép đồng dạng trong mặt phẳng.

Đây là tài liệu cực kì hữu ích, gồm 69 trang phân dạng và tuyển chọn bài tập chuyên đề phép dời hình và phép đồng dạng trong mặt phẳng thuộc chương trình Hình học 11 chương 1. Sau đây là nội dung chi tiết mời các bạn cùng tham khảo và tải tài liệu tại đây.

Chuyên đề
phép dời hình và phép đồng dạng trong mặt phẳng

L
A
T
E
X by NHÓM W-T-TEX-BEGINNING
Mục lục
1 Phép dời hình và phép đồng dạng 3
1.1 PHÉP TỊNH TIẾN . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
1.1.1 Tóm tắt lí thuyết . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
1.1.2 Các dạng toán và ví dụ mẫu . . . . . . . . . . . . . . . . . . . . . . . . . 4
Dạng 1. Tìm ảnh, tạo ảnh của đường thẳng d qua một phép tịnh tiến theo véc-tơ
#»
v . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
Dạng 2. Tìm tạo ảnh của đường thẳng d qua một phép tịnh tiến theo véc-tơ
#»
v . 5
Dạng 3. Tìm ảnh của đường tròn (C) qua một phép tịnh tiến theo véc-tơ
#»
v . . 5
Dạng 4. Tìm tạo ảnh của đường tròn (C
0
) qua một phép tịnh tiến theo véc-tơ
#»
v 5
Dạng 5. Tìm ảnh của một đường cong (P ) qua một phép tịnh tiến theo
#»
u = (a; b) 5
Dạng 6. Tìm tạo ảnh của một đường cong (P) qua một phép tịnh tiến theo
#»
u = (a; b) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
Dạng 7. Xác định véc-tơ tịnh tiến . . . . . . . . . . . . . . . . . . . . . . . . . . 6
Dạng 8. Ứng dụng phép tịnh tiến vào các bài toán hình học sơ cấp . . . . . . . . 6
Dạng 9. Các bài toán thực tế . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
1.1.3 Bài tập trắc nghiệm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
1.2 PHÉP QUAY . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
1.2.1 Tóm tắt lí thuyết . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
1.2.2 Các dạng bài tập tự luận . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
Dạng 1. Cho trước hình (H). Tìm ảnh của điểm, đoạn thẳng, tam giác,. ..liên
quan đến hình (H) qua phép quay cho trước. . . . . . . . . . . . . . . . 18
Dạng 2. Tìm ảnh, tạo ảnh của điểm qua phép quay Q
(I,α)
, với I(a; b). . . . . . . 19
Dạng 3. Tìm ảnh, tạo ảnh của đường thẳng qua phép quay Q
(I,α)
, với I(a; b). . . 19
Dạng 4. Tìm ảnh, tạo ảnh của đường tròn qua phép quay Q
(I,α)
, với I(a; b). . . . 20
Dạng 5. Tìm ảnh, tạo ảnh của đường cong (H) bất kì (khác dạng 3, 4) qua phép
quay Q
(I,α)
, với I(a,b). . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21
Dạng 6. Ứng dụng phép quay để chứng minh các tính chất hình học. . . . . . . 21
Dạng 7. Ứng dụng phép quay để tìm quỹ tích của điểm . . . . . . . . . . . . . . 22
Dạng 8. Các bài toán thực tế . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
1.2.3 Các dạng bài tập trắc nghiệm . . . . . . . . . . . . . . . . . . . . . . . . 25
Dạng 9. Củng cố định nghĩa và tính chất . . . . . . . . . . . . . . . . . . . . . . 25
Dạng 10. Cho trước hình (H). Tìm các phép quay biến hình (H) thành chính nó. 26
Dạng 11. Cho trước hình (H). Tìm ảnh của điểm, đoạn thẳng, tam giác,.. .liên
quan đến hình (H) qua phép quay cho trước . . . . . . . . . . . . . . . . 26
1.3 PHÉP DỜI HÌNH VÀ HAI HÌNH BẰNG NHAU . . . . . . . . . . . . . . . . . 33
1.3.1 Tóm tắt lí thuyết . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33
1.3.2 Các dạng toán tự luận . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33
Dạng 1. Phân biệt phép biến hình và phép dời hình. . . . . . . . . . . . . . . . . 33
Dạng 2. Tìm ảnh, tạo ảnh của một điểm qua một phép dời hình . . . . . . . . . 34
Dạng 3. Tìm ảnh, tạo ảnh của đường thẳng qua một phép dời hình. . . . . . . . 35
Dạng 4. Tìm ảnh, tạo ảnh của đường tròn qua một phép dời hình. . . . . . . . . 35
1
L
A
T
E
X by NHÓM W-T-TEX-BEGINNING
2 MỤC LỤC
Dạng 5. Tìm ảnh, tạo ảnh của một đường cong bất kỳ qua một phép dời hình. . 36
Dạng 6. Sử dụng định nghĩa và các tính chất của phép dời hình để chứng minh
các bài toán hình học. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37
Dạng 7. Bài toán quỹ tích – dựng hình . . . . . . . . . . . . . . . . . . . . . . . 37
Dạng 8. Bài toán min – max . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39
1.3.3 Bài tập tự luận . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39
1.3.4 Đề kiểm tra tự luận . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41
1.3.5 Các dạng toán trắc nghiệm . . . . . . . . . . . . . . . . . . . . . . . . . 42
Dạng 9. Phân biệt phép biến hình và phép dời hình . . . . . . . . . . . . . . . . 42
Dạng 10. Tìm ảnh và tạo ảnh của một điểm qua một phép dời hình . . . . . . . 43
Dạng 11. Tìm ảnh của một đường thẳng qua một phép dời hình . . . . . . . . . 43
Dạng 12. Tìm ảnh, tạo ảnh của hình (H) qua một phép dời hình . . . . . . . . . 44
1.3.6 Bài tập trắc nghiệm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 44
1.3.7 Đề kiểm tra trắc nghiệm . . . . . . . . . . . . . . . . . . . . . . . . . . . 48
1.4 PHÉP VỊ TỰ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 53
1.4.1 Tóm tắt lí thuyết . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 53
1.4.2 CÁC DẠNG BÀI TẬP . . . . . . . . . . . . . . . . . . . . . . . . . . . . 54
Dạng 1. Tìm ảnh, tạo ảnh của một điểm qua một phép vị tự . . . . . . . . . . . 54
Dạng 2. Tìm ảnh, tạo ảnh của đường thẳng qua một phép vị tự . . . . . . . . . 54
Dạng 3. Tìm ảnh, tạo ảnh của một đường tròn qua phép vị tự . . . . . . . . . . 54
Dạng 4. Tìm ảnh, tạo ảnh của một đường cong (khác các dạng trên) qua một
phép vị tự . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 55
Dạng 5. Tìm quỹ tích điểm dựa vào phép vị tự . . . . . . . . . . . . . . . . . . . 55
Dạng 6. Dựng hình dựa vào phép vị tự . . . . . . . . . . . . . . . . . . . . . . . 56
Dạng 7. Chứng minh tính chất hình học của hình . . . . . . . . . . . . . . . . . 56
Dạng 8. Xác định tâm vị tự của hai đường tròn . . . . . . . . . . . . . . . . . . 57
1.4.3 BÀI TẬP KIỂM TRA 45 PHÚT . . . . . . . . . . . . . . . . . . . . . . 57
1.4.4 BÀI TẬP TRẮC NGHIỆM . . . . . . . . . . . . . . . . . . . . . . . . . 57
1.4.5 BÀI TẬP TỰ LUYỆN . . . . . . . . . . . . . . . . . . . . . . . . . . . . 60
1.5 PHÉP ĐỒNG DẠNG . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 64
1.5.1 TÓM TẮT LÝ THUYẾT . . . . . . . . . . . . . . . . . . . . . . . . . . . 64
1.5.2 CÁC DẠNG BÀI TẬP TỰ LUẬN . . . . . . . . . . . . . . . . . . . . . 64
Dạng 1. Xác định ảnh của một hình qua một phép đồng dạng . . . . . . . . . . 65
Dạng 2. Xác định ảnh của một hình qua một phép đồng dạng . . . . . . . . . . 65
1.5.3 Các dạng toán . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 65
Dạng 3. Vận dụng lý thuyết . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 65
Dạng 4. Phương pháp tọa độ. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 66
Dạng 5. Nhận dạng phép đồng dạng, nhận dạng hình . . . . . . . . . . . . . . . 66
1.5.4 BÀI TẬP TRẮC NGHIỆM . . . . . . . . . . . . . . . . . . . . . . . . . 67
L
A
T
E
X by NHÓM W-T-TEX-BEGINNING
Chương 1
Phép dời hình và phép đồng dạng
1.1 PHÉP TỊNH TIẾN
1.1.1 Tóm tắt lí thuyết
Định nghĩa 1.
Trong mặt phẳng cho véc-tơ
#»
v . Phép biến hình biến mỗi điểm M
thành điểm M
0
sao cho
# »
MM
0
=
#»
v được gọi là phép tịnh tiến theo
véc-tơ
#»
v .
N
M
#»
v
Phép tịnh tiến theo véc-tơ
#»
v thường được lí hiệu là T
#»
v
,
#»
v được gọi là véc-tơ tịnh tiến.
Như vậy, T
#»
v
(M) = M
0
⇔
# »
MM
0
=
#»
v .
Phép tịnh tiến theo véc-tơ - không chính là phép đồng nhất. (Biến mỗi điểm thành chính nó).
Tính chất 1.
Biến một véc-tơ thành véc-tơ bằng nó. Nếu T
#»
v
(M) = M
0
,
T
#»
v
(N) = N
0
thì
# »
M
0
N
0
=
# »
MN. Biến đoạn thẳng thành đoạn
thẳng bằng nó M
0
N
0
= MN.
M
0
N
0
M
N
#»
v
#»
v
#»
v
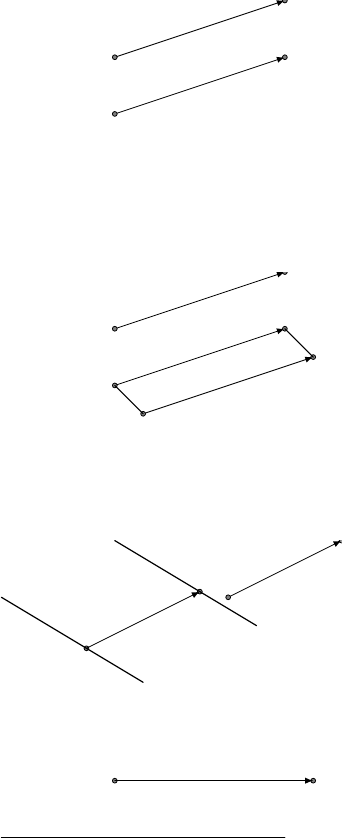
Tính chất 2. Phép tịnh tiến biến đường thẳng thành đường thẳng song song hoặc trùng với
nó.
Dựng ảnh đường thẳng d qua T
#»
v
.
a) Lấy trên d một điểm A.
b) Dựng A
0
là ảnh của A.
c) Qua A
0
dựng đường thẳng cùng phương với d.
A
0
A
d
#»
v
#»
v
d
0
Đặc biệt: d
0
≡ d khi và chỉ khi
#»
v cùng phương với
véc-tơ chỉ phương của d (hay
#»
v có giá song song hoặc
trùng với d).
d
0
≡ d
#»
v
Tính chất 3.
• Biến tam giác thành tam giác bằng nó.
3
Chia sẻ bởi: 👨 Trịnh Thị Thanh
Liên kết tải về

Link Download chính thức:

Tìm thêm: Toán 11

Có thể bạn quan tâm

Xem thêm
Sắp xếp theo
👨

  • Hướng dẫn tìm công thức truy hồi của dãy số

     🖼️

  • Góc giữa hai mặt phẳng: Định nghĩa, cách xác định và Bài tập (có đáp án)

     🖼️

  • Bộ đề thi khảo sát chất lượng đầu năm môn Toán lớp 11 năm 2023 - 2024

     🖼️

  • Phương trình tiếp tuyến

     🖼️

  • Toán 11 Bài 17: Hàm số liên tục

     🖼️

  • Phiếu bài tập cuối tuần Toán 11

     🖼️

  • Bài tập đường thẳng và mặt phẳng trong không gian, quan hệ song song

     🖼️

  • Giá trị lớn nhất, nhỏ nhất của hàm số lượng giác

     🖼️

  • Tính tuần hoàn của hàm số lượng giác

     🖼️
    • Chỉ thành viên Download Pro tải được nội dung này! Download Pro - Tải nhanh, website không quảng cáo! Tìm hiểu thêm
    Mua Download Pro 79.000đ