Đề thi thử vào lớp 10 năm 2019 – 2020 trường THPT Thạch Thành 1, Thanh Hóa Đề thi tuyển sinh vào lớp 10 môn Toán năm 2019
Đề thi thử vào lớp 10 năm 2019 – 2020 trường THPT Thạch Thành 1, Thanh Hóa là tài liệu ôn thi vào lớp 10 hữu ích dành cho các bạn học sinh lớp 9.
Việc luyện tập với đề thi sẽ giúp các bạn củng cố lại kiến thức và rút kinh nghiệm trong quá trình làm bài thi xét tuyển vào lớp 10 sắp tới. Sau đây là nội dung chi tiết, mời các bạn tham khảo và tải tài liệu tại đây.
Đề thi thử vào lớp 10 năm 2019 – 2020 môn Toán
TRƯỜNG THPT THẠCH THÀNH I ĐỀ THI MÔN TOÁN_ KHỐI 10 (lần 2)
Năm học: 2018 – 2019
Thời gian: 120 phút
Câu 1 (1,0 điểm=0,5+0,5):
a) Hãy phát biểu mệnh đề phủ định của mệnh đề sau:
P
: “Có một học sinh của lớp không thích học môn Toán”
b) Cho các tập hợp
1;2;3 , 2;3;4;5
A B
. Xác định các tập hợp sau:
,
A B A B
.
Câu 2 (1,0 điểm=0,5+0,5): Giải các phương trình sau:
a)
2
9
1 1
x
x x
; b)
3 2 3 2x x
.
Câu 3 (1,0 điểm): Tìm
, ,a b c
biết parabol
2
y ax bx c
có đỉnh
1;4
I
và cắt trục
tung tại điểm có tung độ bằng 6.
Câu 4 (1,0 điểm=0,5+0,5): a) Cho hình bình hành
ABCD
và một điểm
M
tùy ý.
Chứng minh rằng:
MB MA DM MC
.
b) Trong mặt phẳng hệ tọa độ
Oxy
, cho tam giác
ABC
với
1; 2 , 2; 11
B C
. Gọi
,M N
là các điểm thỏa mãn
3 , 3
AB AM AC AN
. Hãy tìm tọa độ của véctơ
MN
.
Câu 5 (2,0 điểm=1+1):
Cho hàm số
2
2 1 2 1
y x m x m
(với
m
là tham số thực) (1)
a) Lập bảng biến thiên và vẽ đồ thị hàm số (1) khi
1
m
.
b) Tìm tất cả các giá trị của tham số
m
để đồ thị hàm số (1) cắt trục hoành tại hai
điểm phân biệt
,A B
sao cho diện tích tam giác
HAB
bằng 3, với
H
là giao
điểm của đồ thị hàm số (1) và trục tung.
Câu 6 (2,0 điểm=0,5+0,75+0,75):
Cho tam giác
ABC
có chiều cao
6 , 3 ,AH a HB a
2 0 ,HC a a H
nằm trên cạnh
BC
.
a) Phân tích véctơ
AH
theo hai véctơ
,AB AC
.
b) Tính số đo của góc
BAC
.
c) Gọi
,D E
lần lượt là hình chiếu vuông góc của
H
lên
,AB AC
. Tính độ dài đoạn
thẳng
DE
theo
a
.
Câu 7 (2,0 điểm=1+1):
a) Tìm tất cả các giá trị của tham số thực
m
để phương trình sau vô nghiệm:
1 1
2
x x
x m x
.
b) Cho
0, 0, 6
x y x y
. Tìm giá trị nhỏ nhất của biểu thức
6 8
3 2P x y
x y
.
-------------Hết-------------
ĐÁP ÁN MÔN TOÁN_KHỐI 10
Câu
Nội dung
Điểm
1
a)
:P
”Tất cả học sinh của lớp đều thích học môn Toán”
0,5
b)
2;3
A B
,
1;2;3;4;5
A B
0,5
2
a) Điều kiện
1
x
0,25
Với điều kiện đó, pt
2
9 3
x x
0,25
b) TH 1:
2
1
3
5
3 2 3 2
x
x
x x
0,25
TH 2:
2
5
3
3 2 3 2
x
x
x x
Pt đã cho có hai nghiệm
1
; 5
5
x x
0,25
3
Từ giả thiết ta có hệ pt
1
2
4
6
b
a
a b c
c
0,5
Giải hệ ta được
2, 4, 6
a b c
0,5
4
a)
MB MA AB DC DM MC
0,5
b)
1
3 3 3 3
3
BC AC AB AN AM AN AM MN MN BC
0,25
Mà
3; 9
BC
nên
1; 3
MN
0,25
5
a) Khi
1
m
, ta có
2
4 3y x x
.
Bảng biến thiên (học sinh tự làm)
0,5
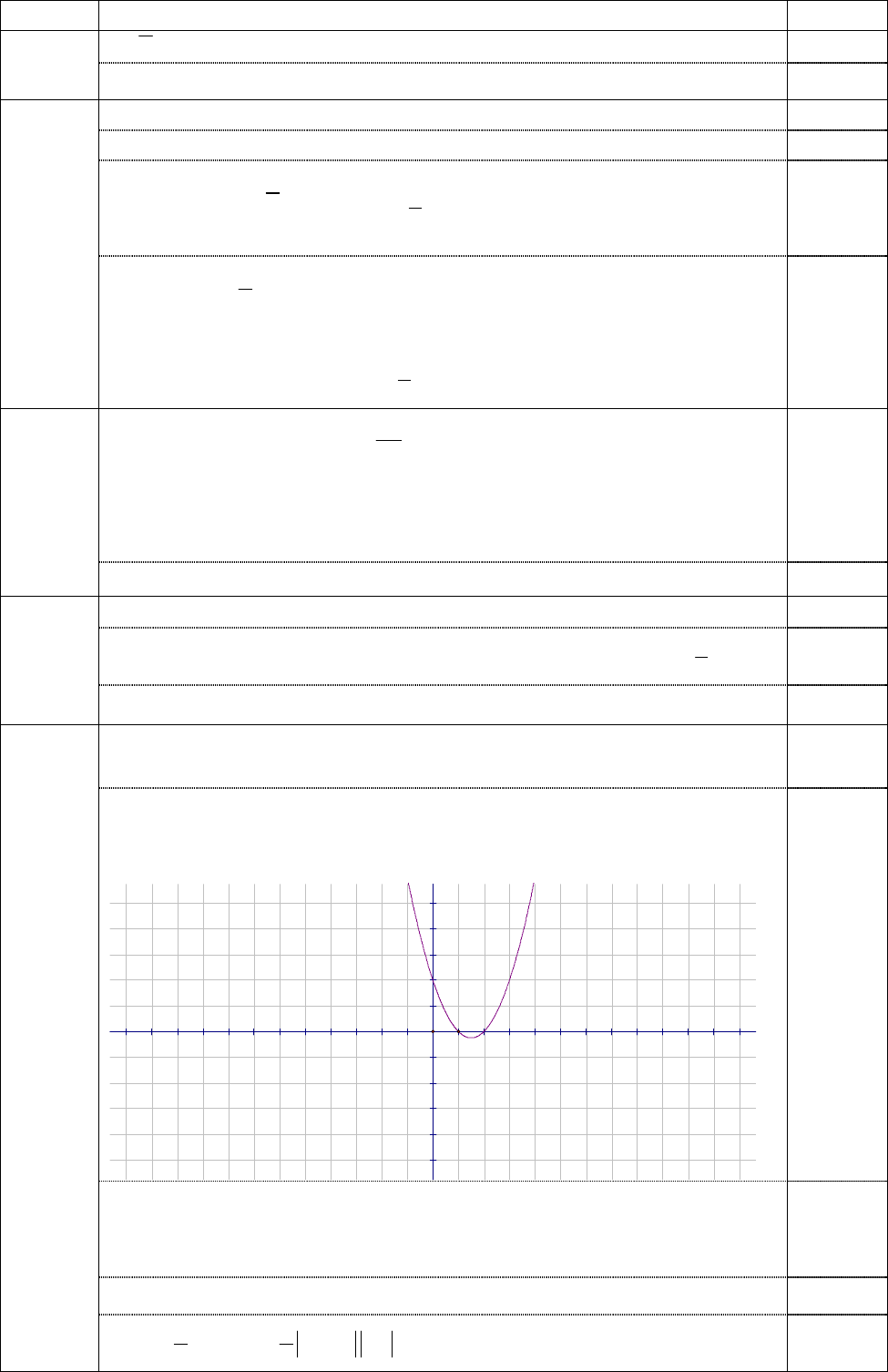
Đồ thị là đường parabol có đỉnh
2; 1
I
, trục đối xứng là đường
thẳng có pt x=2; parabol cắt trục Ox tại các điểm (1;0), (3;0);
parabol cắt trục tung tại điểm (0;3).
4
2
-2
-4
-10 -5 5 10
f x
= x
2
-3
x
+2
0,5
b) Pt hoành độ giao điểm:
2
1
2 1 2 1 0 0
2 1
x
x m x m m
x m
0,25
0; 2 1
H m
0,25
1 1
. 2 1 2 3
2 2
HAB
S OH AB m m
0,25
2
1
2 3
3
2
m
m m
m
0,25
6
a) Từ giả thiết, ta có
3
5
BH BC
.
0,25
3 3 2 3
5 5 5 5
AH AB BH AB BC AB AC AB AB AC
0,25
b) Áp dụng định lí Pitago cho các tam giác vuông HAB, HAC ta
được:
3 5 , 2 10AB a BC a
.
0,25
Từ đó
2 2 2 2 2 2
45 40 25 1
os
2 .
2.3 5 .2 10 2
AB AC BC a a a
c BAC
AC AB
a a
0,25
Vậy
45
BAC
0,25
c) Dựa vào
2 2
. , .AH AD AB AH AE AC
tính được
12 18
,
5 10
a a
AD AE
0,25
Áp dụng định lí côsin cho tam giác
ADE
, ta được
2 2 2
2 2 2
144 18 12 18 2
2 . cos 2. . .
5 10 2
5 10
a a a a
DE AD AE AD AE DAE
0,25
=
2
18 3 2a DE a
.
0,25
7
a) Điều kiện:
, 2
x m x
.
Với đk đó, pt
1 2 1 2
x x x m x mx m
0,5
Pt vô nghiệm
0
2 0
m
m
hoặc
0
2
m
m
x m
m
hoặc
0
2
2
m
m
x
m
0,25
0; 1;2
m
0,25
6 8 3 6 1 8 3
3 2
2 2 2
P x y x y x y
x y x y
0,5
3 6 1 8 3
2 . 2 . .6 19
2 2 2
P x y
x y
.
0,25
Hơn nữa khi
2, 4
x y
(thỏa mãn) thì
19
P
. Vậy
min 19
P
khi
2, 4
x y
0,25
Chia sẻ bởi: 
Trịnh Thị Thanh
Trịnh Thị Thanh Liên kết tải về
Link Download chính thức:
Đề thi thử vào lớp 10 năm 2019 – 2020 trường THPT Thạch Thành 1, Thanh Hóa Download
Có thể bạn quan tâm
-
Văn mẫu lớp 9: Đóng vai ngư dân kể lại bài thơ Đoàn thuyền đánh cá
-
Bài thơ Lượm - Sáng tác năm 1949, Tố Hữu
-
Mẫu 09/ĐK: Đơn đăng ký biến động đất đai
-
Tranh tô màu Pikachu - Bộ tranh tô màu Pikachu đẹp
-
Giáo án Toán lớp 1 (Sách mới) - Giáo án Toán lớp 1 (trọn bộ 5 sách)
-
Tuyển tập đề thi học sinh giỏi môn Toán lớp 3
-
Thuyết minh về Thành Cổ Loa (2 Dàn ý + 5 mẫu)
-
Bộ tranh tô màu chủ đề gia đình cho bé
-
Văn mẫu lớp 10: Phân tích tác phẩm Hiền tài là nguyên khí của quốc gia (2 Dàn ý + 10 Mẫu)
-
Những vần thơ hay - Tuyển tập những bài thơ hay
Sắp xếp theo
