Bộ đề thi thử vào lớp 10 năm 2019 - 2020 phòng GD&ĐT Ba Đình, Hà Nội Đề thi minh họa vào lớp 10 môn Toán có đáp án
Nhằm giúp các bạn học sinh lớp 9 ôn tập và chuẩn bị tốt nhất cho kỳ thi vào lớp 10 sắp tới, Eballsviet.com xin giới thiệu đến các bạn Bộ đề thi thử vào lớp 10 năm 2019 - 2020 phòng GD&ĐT Ba Đình, Hà Nội có đáp án chi tiết kèm theo.
Tài liệu bao gồm đề thi môn Toán kèm theo đáp án. Hi vọng, đề thi này sẽ giúp các bạn luyện tập và làm quen với cấu trúc đề thi môn Toán. Chúc các bạn ôn tập tốt và thi đạt kết quả cao!
Đề thi tuyển sinh vào lớp 10 môn Toán
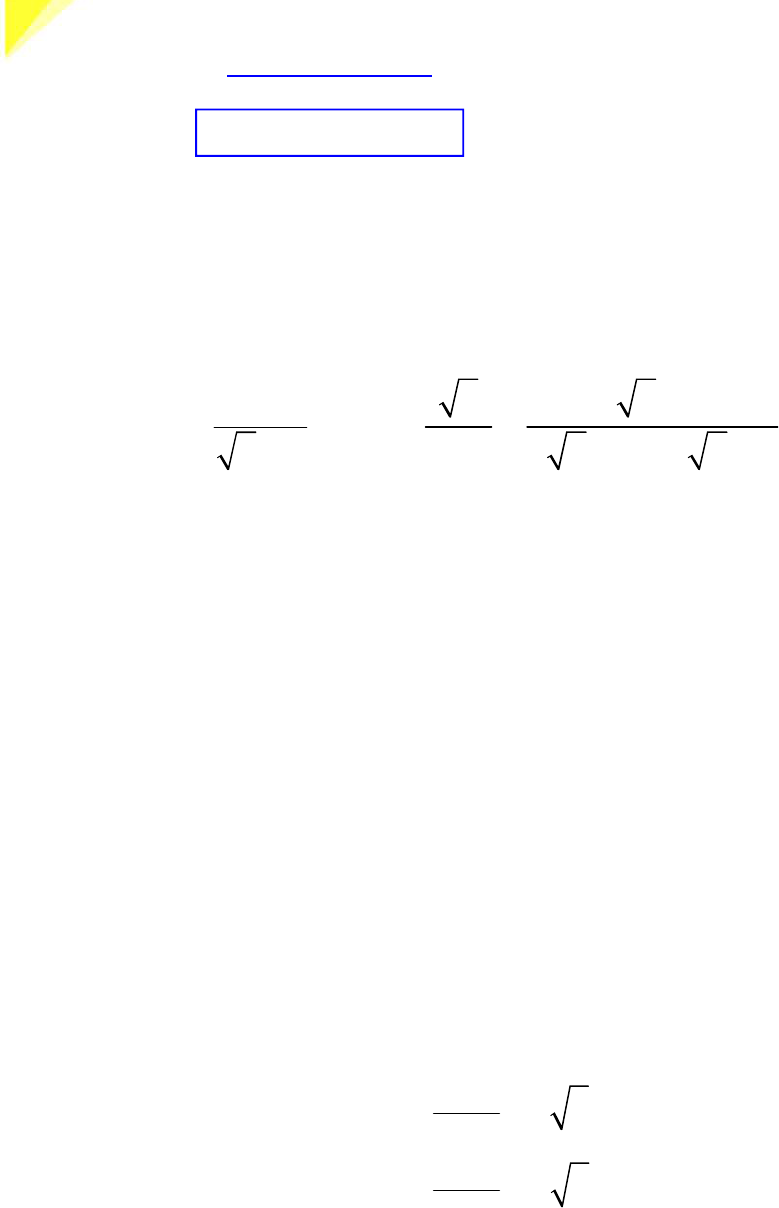
1/1
6
GV: Nguyễn Hữu Phúc
0888.014.879
https://chiasefull.com https://youtube.com/nguyenhuuphuc2017
PHÒNG GD & ĐT QUẬN BA ĐÌNH
ĐỀ KHẢO SÁT CHẤT LƯỢNG MÔN TOÁN 9
Năm học: 2018 – 2019
Ngày khảo sát: 7/5/2019
Thời gian làm bài: 120 phút
Bài I. (2,0 điểm)
Cho hai biểu thức:
=
−
2
2
A
x
và
+
= −
+
− + −
4 2
1
2 2
x x
B
x
x x x x
với
≥ ≠0; 4x x
1) Tính giá trị của biểu thức
A
khi
= 16
x
.
2) Rút gọn biểu thức
= +P A B
.
3) Tìm giá trị của
x
để biểu thức
P
đạt giá trị lớn nhất.
Bài II. (2,0 điểm)
Giải bài toán bằng cách lập phương trình hoặc hệ phương trình:
Một phòng họp có 300 ghế ngồi, được xếp thành một số hàng có số
ghế bằng nhau. Buổi họp hôm đó có 378 người đến dự họp nên ban tổ
chức đã kê thêm 3 hàng ghế và mỗi hàng ghế phải xếp thêm 1 ghế, mới
đủ chỗ ngồi. Hỏi lúc đầu phòng họp có bao nhiêu hàng ghế và mỗi hàng
ghế có bao nhiêu ghế, biết số hàng ghế ban đầu không vượt quá 20.
Bài III. (2,0 điểm)
1) Giải hệ phương trình:
+ =
−
− =
−
2
2 8
1
11
3 2
1
y
x
y
x
2) Cho phương trình:
− − − + =
2
( 3) 2 0x m x m
(
x
là ẩn số)
a) Chứng minh rằng phương trình luôn có nghiệm với mọi giá trị của
m
.
b) Tìm
m
để phương trình có ít nhất một nghiệm dương.
ĐỀ CHÍNH THỨC
2/1
6
GV: Nguyễn Hữu Phúc
0888.014.879
https://chiasefull.com https://youtube.com/nguyenhuuphuc2017
Bài IV. (0,5 điểm)
Một hình cầu có thể tích là
π
3
288 ( )cm
. Tính diện tích mặt cầu đó.
Bài V. (3,0 điểm)
Cho đường tròn
( ; )O R
và dây
BC
cố định (
<
2
BC R
),
BF
là đường
kính.
A
là điểm di chuyển trên cung lớn
BC
(
A
khác
,B C
) sao cho tam
giác
ABC
có ba góc nhọn, các đường cao
AD
và
CE
của tam giác
ABC
cắt nhau tại
H
.
1) Chứng minh tứ giác
AEDC
là tứ giác nội tiếp.
2) Chứng minh
HF
đi qua trung điểm
G
của đoạn thẳng
AC
.
3) Chứng minh
sin
AF
DEC
không đổi.
4) Cho
= 1,5BC R
, gọi
I
là hình chiếu của
G
trên
AB
. Hãy tính bán
kính đường tròn ngoại tiếp tam giác
IBC
theo
R
.
Bài VI. (0,5 điểm)
Cho
,x y
là các số thực dương thỏa mãn
+ ≤ 3x y
. Tìm giá trị nhỏ nhất
của biểu thức
= +
+
2 3
3 1
A
xy y
.
3/1
6
GV: Nguyễn Hữu Phúc
0888.014.879
https://chiasefull.com https://youtube.com/nguyenhuuphuc2017
HƯỚNG DẪN GIẢI
Bài I. (2,0 điểm)
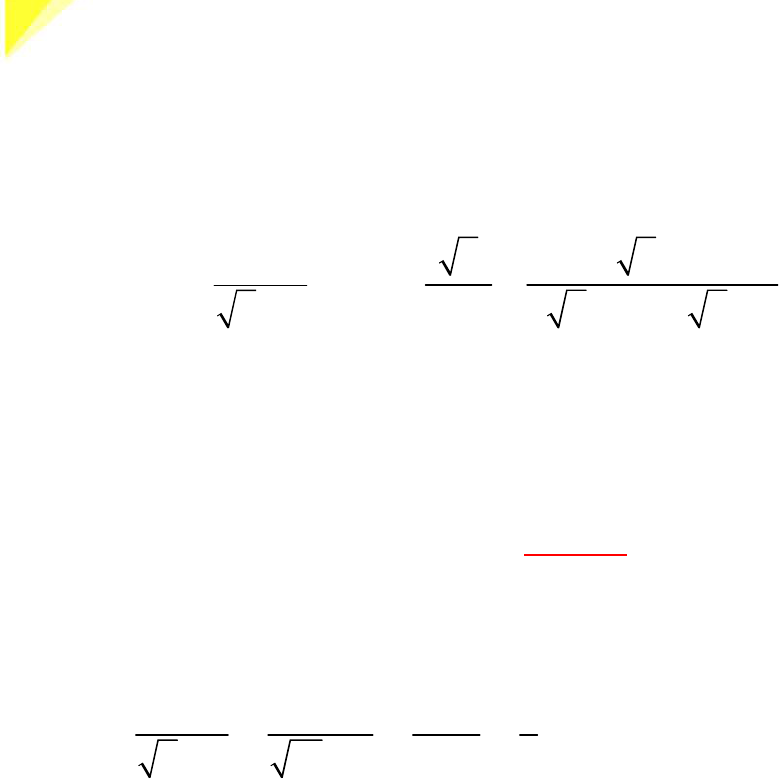
Cho hai biểu thức:
=
−
2
2
A
x
và
+
= −
+
− + −
4 2
1
2 2
x x
B
x
x x x x
với
≥ ≠0; 4x x
1) Tính giá trị của biểu thức
A
khi
= 16x
.
2) Rút gọn biểu thức
= +P A B
.
3) Tìm giá trị của
x
để biểu thức
P
đạt giá trị lớn nhất.
Lời giải
1) Tính giá trị của biểu thức
A
khi
= 16x
.
Thay
= 16x
(thỏa mãn điều kiện xác định) vào biểu thức
A
, ta được:
= = = = =
−
− −
2 2 2 2
1
4 2 2
2 16 2
A
x
Chia sẻ bởi: 
Trịnh Thị Thanh
Trịnh Thị Thanh Liên kết tải về
Link Download chính thức:
Bộ đề thi thử vào lớp 10 năm 2019 - 2020 phòng GD&ĐT Ba Đình, Hà Nội Download
Có thể bạn quan tâm
-
Thuyết minh về cây bút chì (Dàn ý + 9 mẫu)
-
Văn mẫu lớp 8: Phân tích bài thơ Ngắm trăng của Hồ Chí Minh (Sơ đồ tư duy)
-
Bài dự thi những tấm gương tâm huyết sáng tạo học theo lời Bác năm 2023
-
Tập làm văn lớp 5: Tả cảnh bình minh trên quê hương em
-
Văn mẫu lớp 7: Cảm nghĩ về ngày Tết cổ truyền quê em
-
Văn mẫu lớp 9: Đóng vai ngư dân kể lại bài thơ Đoàn thuyền đánh cá
-
Bài thơ Lượm - Sáng tác năm 1949, Tố Hữu
-
Mẫu 09/ĐK: Đơn đăng ký biến động đất đai
-
Tranh tô màu Pikachu - Bộ tranh tô màu Pikachu đẹp
-
Giáo án Toán lớp 1 (Sách mới) - Giáo án Toán lớp 1 (trọn bộ 5 sách)
Sắp xếp theo
