Bài toán tính góc giữa hai mặt phẳng lớp 12 Phương pháp tính góc giữa hai mặt phẳng
Với mong muốn đem đến cho các bạn có thêm nhiều tài liệu ôn tập môn Toán lớp 12, Eballsviet.com xin giới thiệu Bài toán tính góc giữa hai mặt phẳng.
Bài toán tính góc giữa hai mặt phẳng là bài toán tương đối khó và nằm ở mức vận dụng và vận dụng cao.Bên cạnh những phương pháp truyền thống như dựng hình tạo góc thì trong chủ đề này chúng ta sẽ cùng tìm hiểu tới 3 phương pháp giải quyết các bài toán trắc nghiệm có thể nói gần như mọi bài toán tính góc giữa 2 mặt phẳng mà ta hay gặp. Mời các bạn cùng tham khảo và tải tài liệu tại đây.
Bài toán tính góc giữa hai mặt phẳng lớp 12
v
TẠP CHÍ VÀ TƯ LI
ỆU TOÁN H
ỌC
CƯA ĐỔ HÌNH KHÔNG GIAN
1
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton
BÀI TOÁN TÍNH GÓC GIỮA HAI MẶT PHẲNG
Tạp chí và tư liệu toán học
Bài toán tính góc giữa hai mặt phẳng là những bài toán tương đối khó và nằm ở mức vận
dụng và vận dụng cao, bên cạnh những phương pháp truyền thống như dựng hình tạo góc
thì trong chủ đề của tuần này ta sẽ cùng tìm hiểu tới 3 phương pháp giải quyết các bài toán
trắc nghiệm có thể nói gần như mọi bài toán tính góc giữa 2 mặt phẳng mà ta hay gặp. Bản
pdf được đăng trên blog Chinh phục Olympic toán các bạn chú ý đón đọc nhé!
I. CÁC PHƯƠNG PHÁP XỬ LÝ.
1. SỬ DỤNG CÔNG THỨC HÌNH CHIẾU.
Đây là một tính chất khá là cơ bản trong chương trình hình học 11 mà ta cần nắm rõ, công
thức của nó rất đơn giản như sau.
Nội dung. Cho hình
S
thuộc mặt phẳng
P
, hình
S'
là hình chiếu của S lên mặt phẳng
Q
,
khi đó ta có cosin góc giữa hai mặt phẳng
P
và
Q
được tính theo công thức
S'
cos
S
.
Sau đây là ví dụ minh họa cho công thức này.
Bài toán
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có
AB a;AD 2a
AA' 4a
. Gọi M,N,P lần lượt
thuộc các cạnh AA’, DD’, BB’ sao cho
MA MA'
,
ND 3ND'
,
PB' 3PB
, mặt phẳng
MNP
cắt cạnh CC; tại Q. Tính cosin góc giữa
MNQP ; ABCD
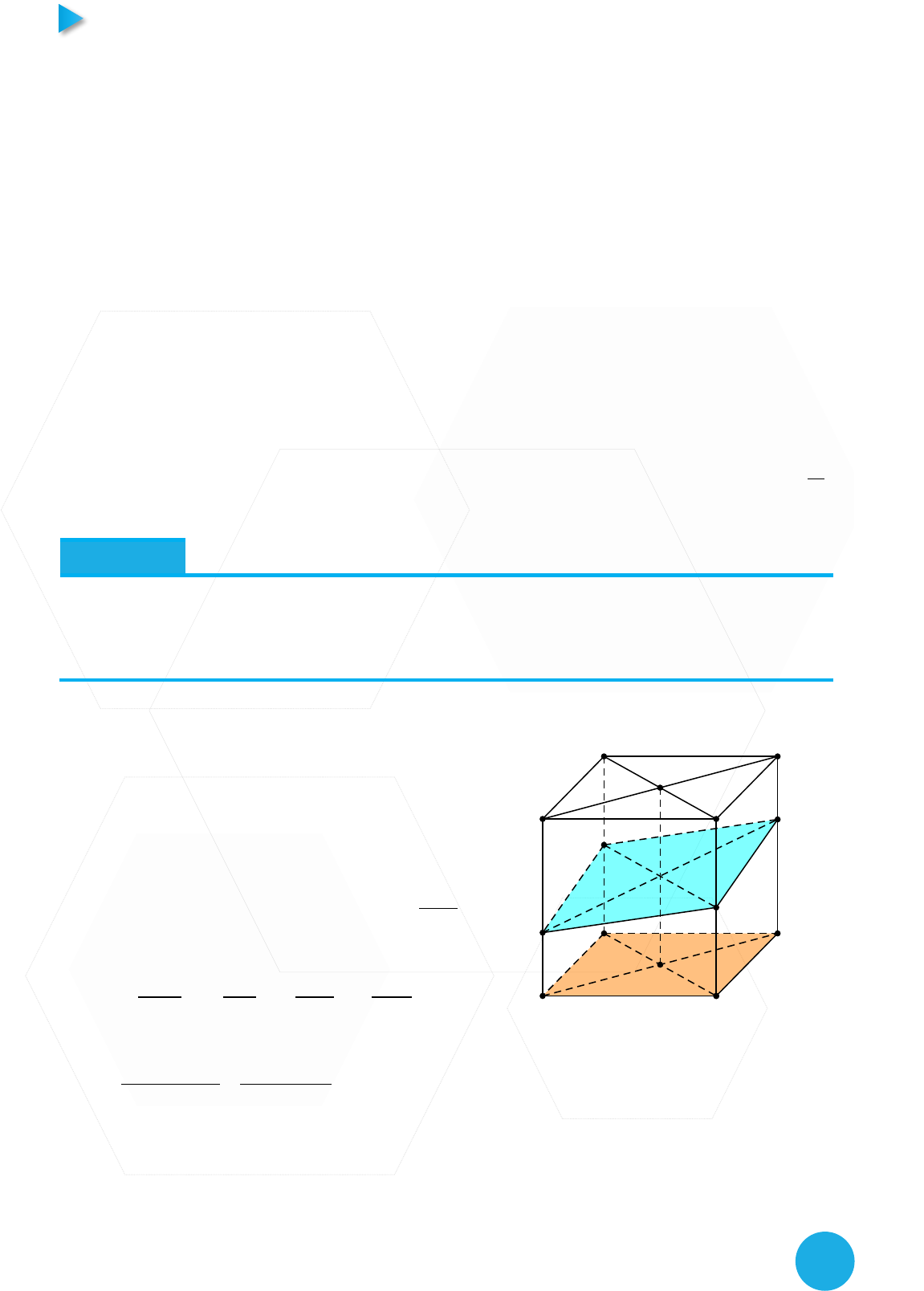
Hướng dẫn
Đầu tiên ta cần phải chú ý tới cách dựng được
điểm Q. Kẻ đường nối tâm 2 đáy
, ta thấy PN
thuộc mặt phẳng
B'D'DB
nên
sẽ cắt PN,
đồng thời P, M, N cùng thuộc mặt phẳng nên nối
M vs giao điểm vừa tìm được ta sẽ ra được điểm
Q. Vấn đề ở đây là ta cần tính được tỷ số
C'Q
CQ
, ta
sẽ sử dụng tới tính chất sau.
Đặt
A'M B'P C'Q D'N
x , y ,z ,t
AA' B'B C'C D'D
, khi đó
ta có 2 công thức cần nhớ sau:
A'B'C'D'.MPQN
A'B'C'D'.ABCD
V
x y z t
V4
x z y t
Q
M
B'
C'
D'
A'
A
D
C
B
P
N
CHINH PH
ỤC OLYMPIC TOÁN
GÓC VÀ KHOẢNG CÁCH
2
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Áp dụng vào bài toán ta suy ra
C'Q 1
CC' 2
. Để ý ta thấy rằng
MN PQ, M P QN
nên MNQP
là hình bình hành. Dễ dàng tính được các đoạn thẳng
2
2
1 1 2 10
MN PQ 4 2
2 3 3
2
2
1 1 13
MP QN 4 1
2 3 3
Mặt khác do
MQ
là đường trung bình của
22
1 1 5
A'C'CA MQ AC 1 2
2 2 2
Từ đây dùng công thức Herong dễ dàng tính được
MNQP
599
S
48
Mặt khác hình chữ nhật ABCD chính là hình chiếu của hình bình hành MNQP lên mặt phẳng
ABCD
nên áp dụng công thức cần ta có
ABCD
MNQP
S
599
cos MNQP ; ABCD
S 96
2. SỬ DỤNG CÔNG THỨC GÓC NHỊ DIỆN.
Đây là một công cụ rất mạnh để giải quyết các bài toán tính góc giữa 2 mặt phẳng, hầu hết
các bài toán đơn giản hay đến phức tạp đều có thể giải bằng phương pháp này, sau đây ta
sẽ cùng tìm hiểu nó. Trong phần này mình sẽ chỉ hướng dẫn các bước làm cho các bạn!
Các bước thực hiện.
Bước 1: Đưa góc giữa hai mặt phẳng về góc giữa hai mặt phẳng kề nhau của một tứ diện.
Chú ý điều này luôn thực hiện được.
Bước 2: Sử dụng công thức:
12
2S S sin
V
3a
. Trong đó
12
S , S
lần lượt là diện tích hai tam
giác kề nhau của tứ diện, a là độ dài giao tuyến, còn
là góc giữa hai mặt phẳng cần tìm.
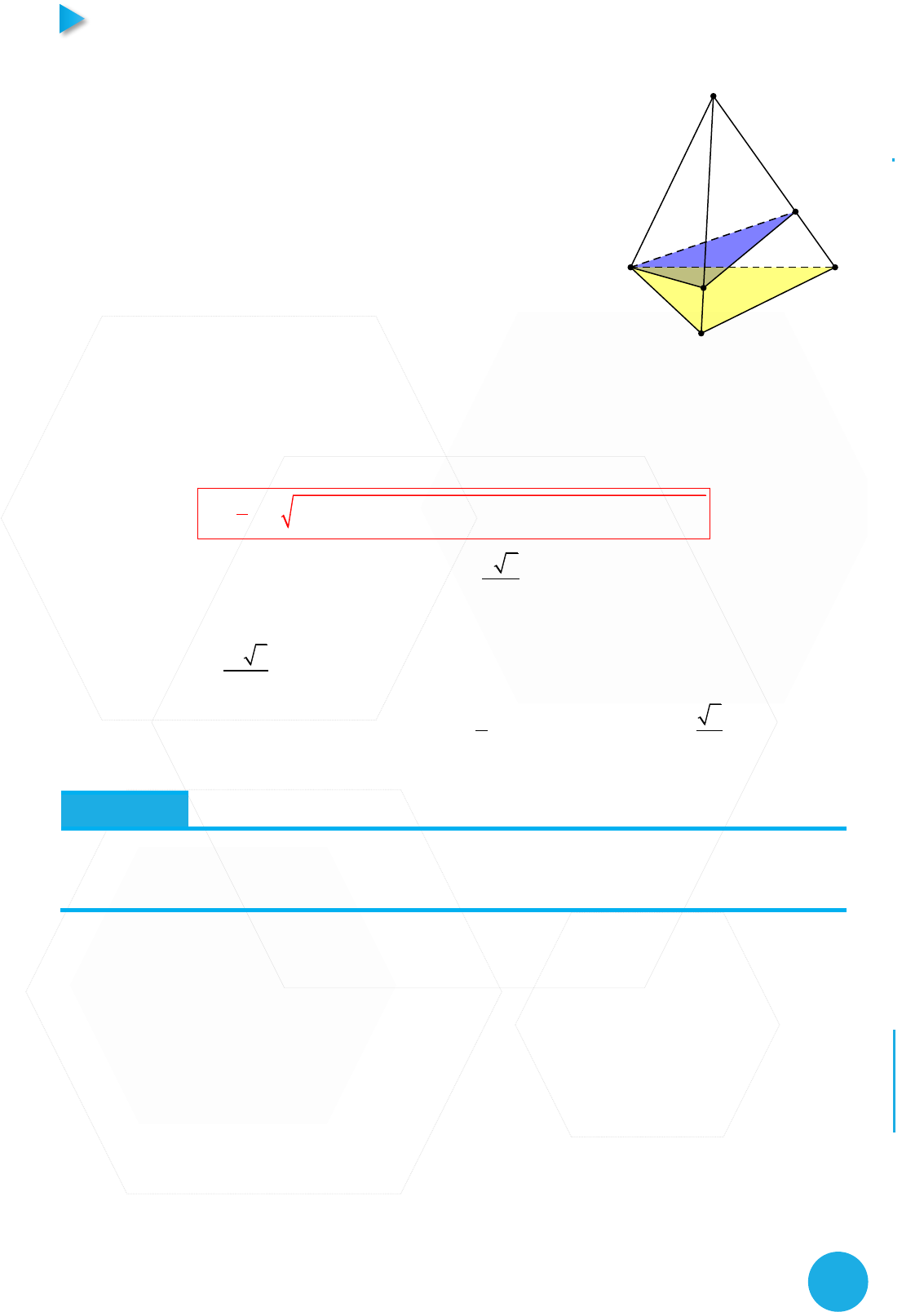
Bài toán
Cho tứ diện S.ABC,
o o o
SA a; SB 2a;SC 3a;ASB 60 ;BSC 90 ;CSA 120
. Tính cosin
SAB ; SBC
.
Hướng dẫn
v
TẠP CHÍ VÀ TƯ LI
ỆU TOÁN H
ỌC
CƯA ĐỔ HÌNH KHÔNG GIAN
3
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton
Yêu cầu của đề bài là tính góc giữa hai mặt phẳng thì theo
như bước 1 ta phải đưa về một tứ diện với bài này thì khỏi
nhỉ bởi nó đã thuộc 1 tứ diện sẵn rồi . Giờ ta phải tính
thể tích của khối tứ diện đó. Đầu tiên thì phải chú ý đến
giả thiết, với những bài mà cho độ dài các cạnh bên với
lại góc ý thì ta phải dựng một chóp tam giác đều khác
bằng cách lấy trên SB,SB các điểm B’, C’ sao cho
SB' a, SC' a
thì ta được S.AB’C’ là chóp tam giác đều
và ta sẽ tính được thể tích của nó, xong sau đótìm dùng
công thức tỷ số thể tích sẽ tính được
S.ABC
V
.
Đó là cách làm truyền thống, còn đối với thi trắc nghiệm thì có thể nhớ công thức tính thể
tích như sau:
Tứ diện S.ABC có
SA a, SB b, SC c,ASB ,BSC ,CSA
thì thể tích của nó là:
2 2 2
1
V abc 1 2 cos cos cos cos cos cos
6
Áp dụng vào bài ta tính được thể tích là
S.ABC
a2
V
2
.
Đồng thời có giả thiết góc thì suy ra tất cả các cạnh của nó ta sẽ tính được diện tích của hai
tam giác là:
2
2
SAB SBC
a3
S ;S 3a ;SB 2
2
.
Tương vào công thức ta có
23
sin SAB ; SBC cos SAB ; SBC
33
.
Xong bài nhé! đơn giản không nào.
Bài toán
Cho tứ diện ABCD,
oo
BC 3, CD 4,ABC BCD ADC 90 , AD,BC 60
. Tính
cos ABC ; ACD
.
Hướng dẫn
Một bài toán tương đối khó phải không nào?
A
C
B
S
B'
C'
Chia sẻ bởi: 
Trịnh Thị Thanh
Trịnh Thị Thanh Liên kết tải về
Link Download chính thức:
Bài toán tính góc giữa hai mặt phẳng lớp 12 Download
Có thể bạn quan tâm
-
Giáo án Toán lớp 1 (Sách mới) - Giáo án Toán lớp 1 (trọn bộ 5 sách)
-
Tuyển tập đề thi học sinh giỏi môn Toán lớp 3
-
Thuyết minh về Thành Cổ Loa (2 Dàn ý + 5 mẫu)
-
Bộ tranh tô màu chủ đề gia đình cho bé
-
Văn mẫu lớp 10: Phân tích tác phẩm Hiền tài là nguyên khí của quốc gia (2 Dàn ý + 10 Mẫu)
-
Những vần thơ hay - Tuyển tập những bài thơ hay
-
Văn mẫu lớp 9: Nghị luận về hiện tượng học tủ, học vẹt
-
File luyện viết chữ in hoa - Mẫu chữ hoa cho học sinh Tiểu học
-
Đề kiểm tra học kì II môn Toán lớp 1
-
Văn mẫu lớp 7: Phân tích bài Ngẫu nhiên viết nhân buổi mới về quê
Sắp xếp theo
