Toán 12 Bài 8: Biểu thức toạ độ của các phép toán vectơ Giải Toán 12 Kết nối tri thức trang 67 → 72
Giải Toán 12 Bài 8: Biểu thức toạ độ của các phép toán vectơ là tài liệu vô cùng hữu ích giúp các em học sinh có thêm nhiều gợi ý tham khảo để giải các bài tập trong SGK Toán 12 Kết nối tri thức với cuộc sống tập 1 trang 67, 68, 69, 70, 71, 72.
Giải bài tập Toán 12 Kết nối tri thức tập 1 Bài 8 được trình bày rõ ràng, cẩn thận, dễ hiểu nhằm giúp học sinh nhanh chóng biết cách làm bài. Đồng thời, cũng là tài liệu hữu ích giúp giáo viên thuận tiện trong việc hướng dẫn học sinh ôn tập Bài 8 Chương II: Vectơ và hệ trục tọa độ trong không gian. Mời thầy cô và các em theo dõi bài viết dưới đây của Eballsviet.com:
Toán 12 Bài 8: Biểu thức toạ độ của các phép toán vectơ
Giải Toán 12 Kết nối tri thức Tập 1 trang 72
Bài 2.20
không gian Oxyz, cho ba vectơ ![]() \(\vec{a}\) = (3; 1; 2),
\(\vec{a}\) = (3; 1; 2), ![]() \(\vec{b}\) = (− 3; 0; 4) và
\(\vec{b}\) = (− 3; 0; 4) và ![]() \(\vec{c}\) = (6; − 1; 0).
\(\vec{c}\) = (6; − 1; 0).
a) Tìm tọa độ của các vectơ ![]() \(\vec{a} +\vec{b}+\vec{c}\) và
\(\vec{a} +\vec{b}+\vec{c}\) và ![]() \(2\vec{a}-3\vec{b}-5\vec{c}\)
\(2\vec{a}-3\vec{b}-5\vec{c}\)
b) Tính các tích vô hướng ![]() \(\vec{a} .(-\vec{b})\) và
\(\vec{a} .(-\vec{b})\) và ![]() \((2\vec{a}) .\vec{c}\)
\((2\vec{a}) .\vec{c}\)
Hướng dẫn giải:
a) ![]() \(\vec{a} +\vec{b}+\vec{c}\) = (6; 0; 6)
\(\vec{a} +\vec{b}+\vec{c}\) = (6; 0; 6)
![]() \(2\vec{a}-3\vec{b}-5\vec{c}\) = (- 15; 7; - 8)
\(2\vec{a}-3\vec{b}-5\vec{c}\) = (- 15; 7; - 8)
b) ![]() \(\vec{a} .(-\vec{b})=- \vec{a}.\vec{b}=-(-9+0+8)=1\)
\(\vec{a} .(-\vec{b})=- \vec{a}.\vec{b}=-(-9+0+8)=1\)
![]() \((2\vec{a}) .\vec{c} =2\vec{a}.\vec{c}=2(18-1)=34\)
\((2\vec{a}) .\vec{c} =2\vec{a}.\vec{c}=2(18-1)=34\)
Bài 2.21
Trong không gian Oxyz, cho ba điểm M(− 4; 3; 3), N(4; − 4; 2) và P(3; 6; − 1).
a) Tìm tọa độ của các vectơ ![]() \(\overrightarrow{MN},\overrightarrow{MP}\), từ đó chứng minh rằng ba điểm M, N, P không thẳng hàng.
\(\overrightarrow{MN},\overrightarrow{MP}\), từ đó chứng minh rằng ba điểm M, N, P không thẳng hàng.
b) Tìm tọa độ của vectơ ![]() \(\overrightarrow{NM}+\overrightarrow{NP}\), từ đó suy ra tọa độ của điểm Q sao cho tứ giác MNPQ là hình bình hành.
\(\overrightarrow{NM}+\overrightarrow{NP}\), từ đó suy ra tọa độ của điểm Q sao cho tứ giác MNPQ là hình bình hành.
c) Tính chu vi của hình bình hành MNPQ.
Hướng dẫn giải:
a) Ta có: ![]() \(\overrightarrow{MN}\) = (8; - 7; - 1)
\(\overrightarrow{MN}\) = (8; - 7; - 1)
![]() \(\overrightarrow{MP}\) = (7; 3; - 4)
\(\overrightarrow{MP}\) = (7; 3; - 4)
Vì không tồn tại k sao cho ![]() \(\overrightarrow{MP}=k\overrightarrow{MN}\) nên M, N, P không thẳng hàng.
\(\overrightarrow{MP}=k\overrightarrow{MN}\) nên M, N, P không thẳng hàng.
b) Ta có: ![]() \(\overrightarrow{NM}+\overrightarrow{NP}\)
\(\overrightarrow{NM}+\overrightarrow{NP}\)
= (- 8; 7; 1) + (- 1; 10; - 3)
= (- 9; 17; - 2)
Giả sử tọa độ điểm Q là (x; y; z)
Để MNPQ là hình bình hành thì ![]() \(\overrightarrow{NQ}=\overrightarrow{NM}+\overrightarrow{NP}\)
\(\overrightarrow{NQ}=\overrightarrow{NM}+\overrightarrow{NP}\)
Do đó: (x - 4; y + 4; z - 2) = (- 9; 17; - 2)
Vậy x = - 5; y = 13; z = 0 hay Q(- 5; 13; 0)
c) MN = ![]() \(\sqrt{114}\); NP =
\(\sqrt{114}\); NP = ![]() \(\sqrt{110}\)
\(\sqrt{110}\)
Chu vi của hình bình hành là: ![]() \(2\left(\sqrt{114}+\sqrt{110}\right)\)
\(2\left(\sqrt{114}+\sqrt{110}\right)\)
Bài 2.22
Trong không gian Oxyz, cho tam giác ABC có A(1; 0; 1), B(0; − 3; 1) và C(4; − 1; 4).
a) Tìm tọa độ trọng tâm của tam giác ABC.
b) Chứng minh rằng ![]() \(\widehat{BAC} =90^{\circ}\)
\(\widehat{BAC} =90^{\circ}\)
c) Tính ![]() \(\widehat{ABC}\).
\(\widehat{ABC}\).
Hướng dẫn giải:
a) Tọa độ trong tâm G của tam giác ABC là:
![]() \(G\left(\frac{5}{3};-\frac{4}{3};2\right)\)
\(G\left(\frac{5}{3};-\frac{4}{3};2\right)\)
b) ![]() \(\overrightarrow{AB}=(-1;-3;0);\ \overrightarrow{AC}=(3;-1;3)\)
\(\overrightarrow{AB}=(-1;-3;0);\ \overrightarrow{AC}=(3;-1;3)\)
Do ![]() \(\overrightarrow{AB}.\overrightarrow{AC}\) = (- 1) . 3 + (- 3) . (- 1) + 0.3 = 0
\(\overrightarrow{AB}.\overrightarrow{AC}\) = (- 1) . 3 + (- 3) . (- 1) + 0.3 = 0
Nên ![]() \(\overrightarrow{AB}\) vuông góc với
\(\overrightarrow{AB}\) vuông góc với ![]() \(\overrightarrow{AC}\) hay
\(\overrightarrow{AC}\) hay ![]() \(\widehat{BAC} =90^{\circ}\).
\(\widehat{BAC} =90^{\circ}\).
c) ![]() \(\overrightarrow{BA}=(1;3;0);\ \overrightarrow{BC}=(4;2;3)\)
\(\overrightarrow{BA}=(1;3;0);\ \overrightarrow{BC}=(4;2;3)\)
 \(\cos ABC=\frac{\overrightarrow{BA}.\overrightarrow{BC}}{|\overrightarrow{BA}|.|\overrightarrow{BC}|}=\frac{10}{\sqrt{10}.\sqrt{29}}=\frac{\sqrt{290}}{29}\)
\(\cos ABC=\frac{\overrightarrow{BA}.\overrightarrow{BC}}{|\overrightarrow{BA}|.|\overrightarrow{BC}|}=\frac{10}{\sqrt{10}.\sqrt{29}}=\frac{\sqrt{290}}{29}\)
Vậy góc ABC ≈ 54o.
Bài 2.23
Một phòng học có thiết kế dạng hình hộp chữ nhật với chiều dài là 8 m, chiều rộng là 6 m và chiều cao là 3 m. Một chiếc đèn được treo tại chính giữa trần nhà của phòng học. Xét hệ trục tọa độ Oxyz có gốc O trùng với một góc phòng và mặt phẳng (Oxy) trùng với mặt sàn, đơn vị đo được lấy theo mét (H.2.51). Hãy tìm tọa độ của điểm treo đèn.
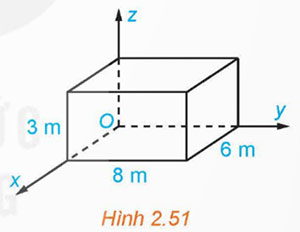
Hướng dẫn giải:
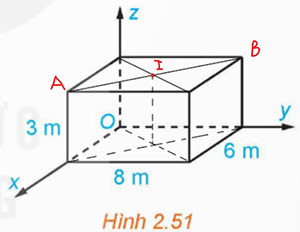
Gọi điểm treo đèn là điểm I(x; y; z), A(6; 0; 3) và B(0; 8; 3) là các điểm có trong hình vẽ.
Do căn phòng là dạng hình hộp chữ nhật nên I là trung điểm của AB.
Vậy tọa độ của điểm treo đèn là I(3; 4; 3).
Bài 2.24
Trong không gian, xét hệ tọa độ Oxyz có gốc O trùng với vị trí của một giàn khoan trên biển, mặt phẳng (Oxy) trùng với mặt biển (được coi là phẳng) với trục Ox hướng về phía tây, trục Oy hướng về phía nam và trục Oz hướng thẳng đứng lên trời (H.2.52). Đơn vị đo trong không gian Oxyz lấy theo kilômét. Một chiếc radar đặt tại giàn khoan có phạm vi theo dõi là 30 km. Hỏi radar có thể phát hiện được một chiếc tàu thám hiểm có tọa độ là (25; 15; − 10) đối với hệ tọa độ nói trên hay không? Hãy giải thích vì sao.

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:













 Đề thi học kì 1 Lớp 12
Đề thi học kì 1 Lớp 12
 Đề thi giữa học kì 1 Lớp 12
Đề thi giữa học kì 1 Lớp 12
 Đề thi giữa học kì 2 Lớp 12
Đề thi giữa học kì 2 Lớp 12
 Đề thi học kì 2 Lớp 12
Đề thi học kì 2 Lớp 12
 Soạn Văn 12 KNTT
Soạn Văn 12 KNTT
 Soạn Văn 12 CTST
Soạn Văn 12 CTST
 Soạn Văn 12 Cánh Diều
Soạn Văn 12 Cánh Diều
 Văn 12
Văn 12
 Toán 12 Chân trời sáng tạo
Toán 12 Chân trời sáng tạo









