14 tính chất thường gặp trong hình học phẳng Tài liệu chinh phục hình học tọa độ phẳng
14 tính chất thường gặp trong hình học phẳng là tài liệu giúp các bạn lớp 10 ôn lại các tính chất trong hình học phẳng và vận dụng nó làm các bài tập dựa theo những tính chất đó.
Tài liệu bao gồm 33 trang kèm theo 36 bài tập minh họa có hướng dẫn giải, vận dụng 14 tính chất đã trình bày để minh họa cụ thể. Hi vọng tài liệu sẽ giúp bạn có được kiến thức tổng hợp và cách nhìn nhận tốt nhất để tư duy giải thành công câu hình học tọa độ phẳng Oxy trong kỳ thi sắp tới. Sau đây là nội dung chi tiết mời các bạn cùng tham khảo và tải tài liệu tại đây.
14 tính chất thường gặp trong hình học phẳng
CHINH PH
ỤC
HÌNH H
ỌC TỌA ĐỘ PHẲNG
Trang
1
Nguồn: http://www.toanmath.com/
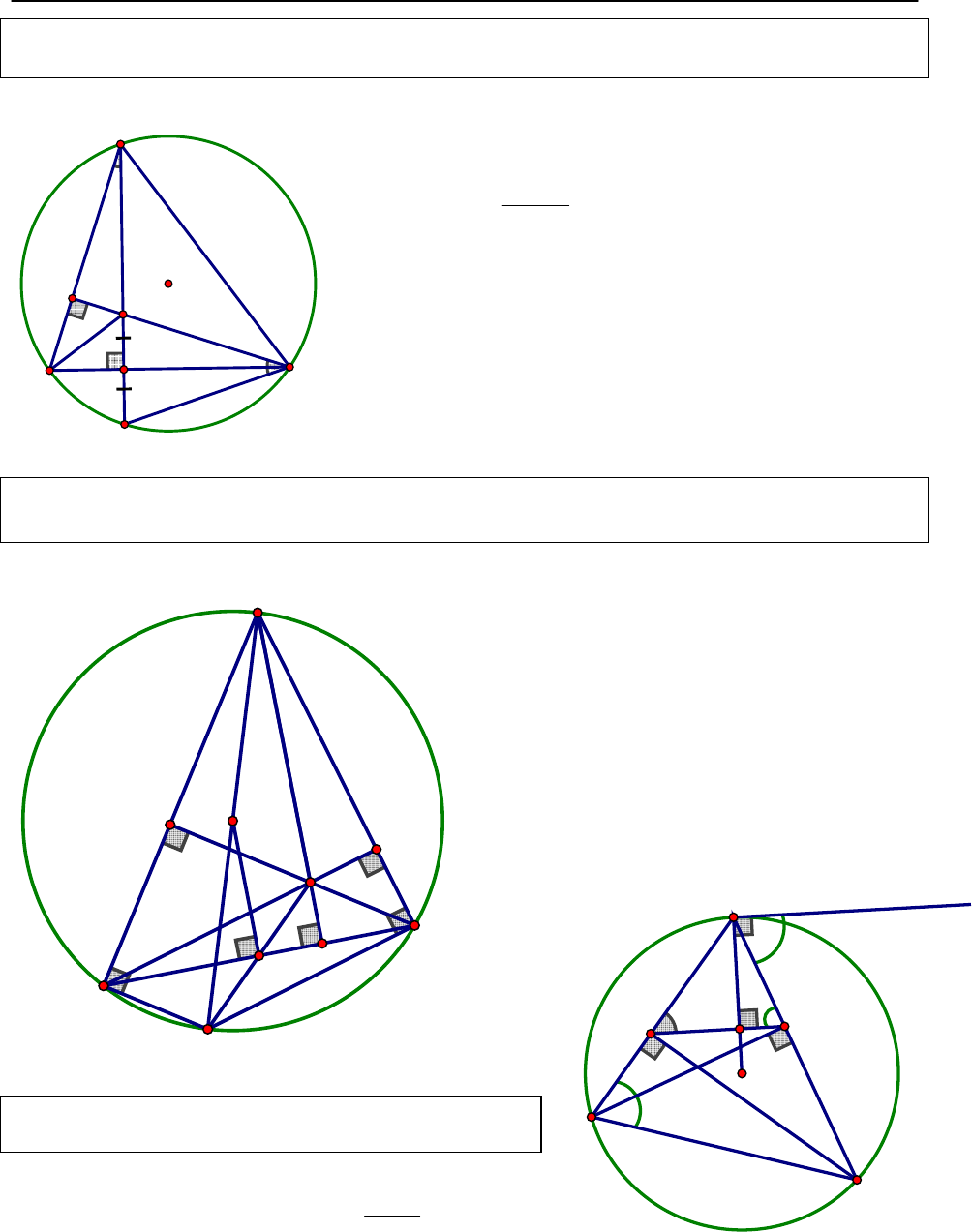
Tính chất 1: Cho
ABC
∆
nội tiếp đường tròn (O), H là trực tâm. Họi H’ là giao điểm của AH
với đường tròn (O)
H '
⇒
đối xứng với H qua BC
Hướng dẫn chứng minh:
+ Ta có Gọi
1
1
A C
=
==
=
(cùng phụ với
ABC
)
+ Mà
1
2 1 2
sdBH '
A C C C
2
= =
= == =
= = ⇒
⇒⇒
⇒ =
==
=
HCH '
⇒
⇒⇒
⇒ ∆
∆∆
∆
cân tại C
⇒
⇒⇒
⇒
BC là trung trực của HH’
H '
⇒
đối xứng với H qua BC
Tính ch
ất 2: Cho
ABC
∆
nội tiếp đường tròn (O), H là trực tâm, kẻ đường kính AA’, M là trung
điểm BC
AH 2.OM
⇒ =
Hướng dẫn chứng minh:
+ Ta có
0
ABA ' 90
= (góc nội tiếp chắn nửa
đường tròn tâm O)
BA BA '
⇒ ⊥
, mà
BA CH BA '/ /CH
⊥ ⇒
(1).
+ Chứng minh tương tự ta cũng có
CA '/ /BH
(2)
+ Từ (1) và (2)
⇒
tứ giác BHCA’ là hình bình
hành, mà M là trung điểm đường chéo BC
⇒
M là trung điểm của đường chéo A’H
OM
⇒
là đường trung bình của
'H AH 2.OM
AA∆ ⇒ =
Tính chất 3: Cho
ABC
∆
nội tiếp đường tròn (O), BH
và CK là 2 đường cao của
ABC
∆
AO KH
⇒ ⊥
Hướng dẫn chứng minh:
+ Kẻ tiếp tuyến Ax
sdAC
xAC ABC
2
⇒ = =
+ Mà
ABC AHK
= (do tứ giá KHCB nội tiếp)
xAC AHK
⇒ = , mà 2 góc này ở vị trí so le trong
/ /HK
Ax
⇒
+ Lại có
Ax AO
⊥
(do Ax là tiếp tuyến)
AO HK
⇒ ⊥
O
2
1
1
H'
C
B
A
H
K
H
O
x
C
B
A
M
A'
C
B
A
O
H
CHINH PH
ỤC
HÌNH H
ỌC TỌA ĐỘ PHẲNG
Trang
2
Nguồn: http://www.toanmath.com/
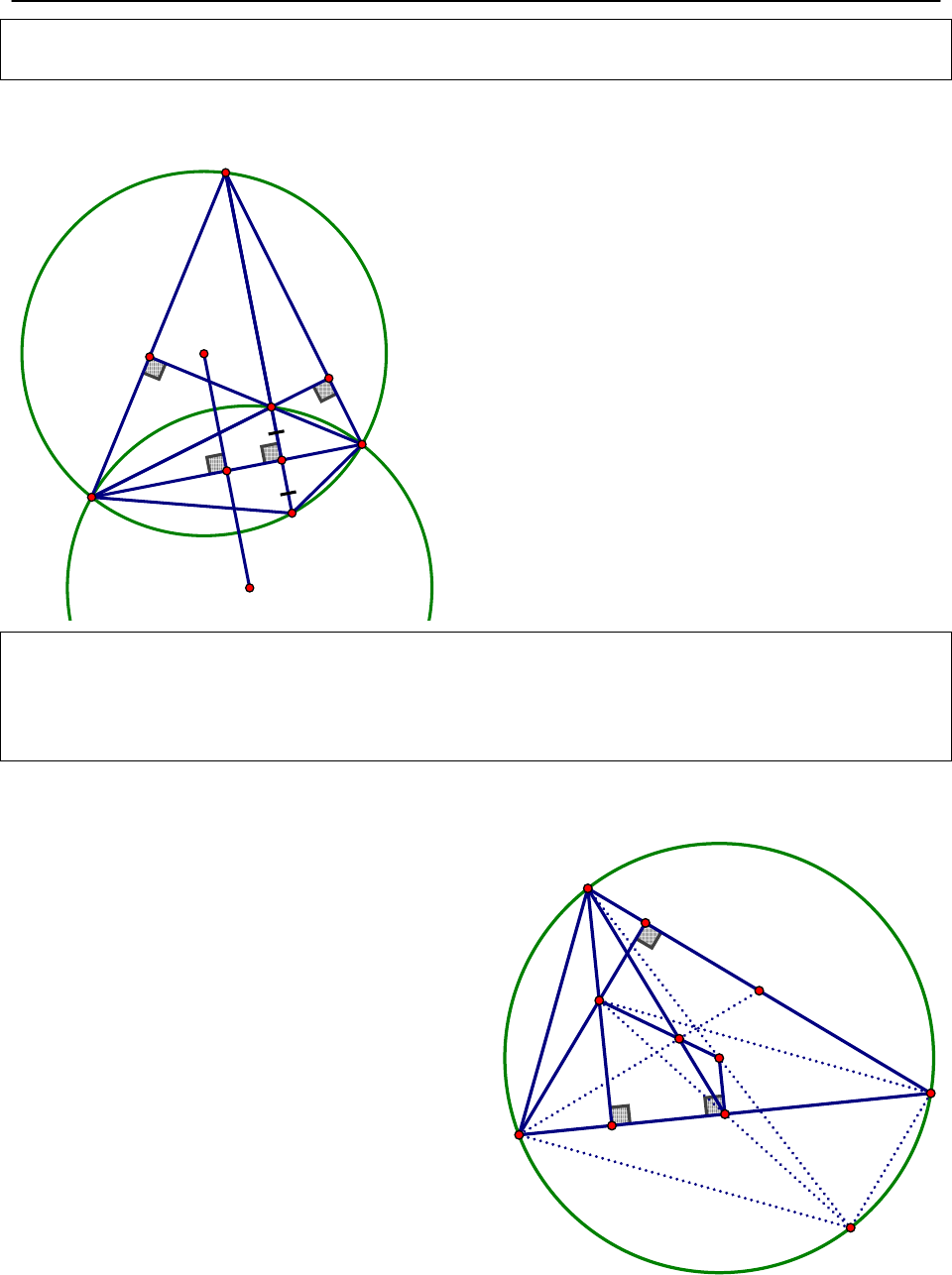
Tính chất 4: Cho
ABC
∆
nội tiếp đường tròn (O), H là trực tâm, gọi I là tâm đường tròn ngoại
tiếp HBC
∆ ⇒
O và I đối xứng nhau qua BC.
Hướng dẫn chứng minh:
+ Gọi H’ là giao điểm của AH với đường tròn (O)
⇒
tứ giác ACH’B nội tiếp đường tròn (O)
⇒
O
đồng thời là tâm đường tròn ngoại tiếp
BH 'C
∆
.
+ Mặt khác H và H’ đối xứng nhau qua BC (tính
chất 1 đã chứng minh)
HBC
⇒ ∆
đối xứng với
H 'BC
∆
qua BC, mà O, I lần lượt là tâm đường
tròn ngoại tiếp
H 'BC
∆
và
HBC
∆
I
⇒
và O đối
xứng nhau qua BC.
Tính chất 5: (Đường thẳng Ơ - le) Cho
ABC
∆
, gọi H, G, O lần lượt là trực tâm, trọng tâm và
tâm đường tròn ngoài tiếp
ABC
∆
. Khi đó ta có:
1).
OH OA OB OC
= + +
2). 3 điểm O, G, H thẳng hàng và
OH 3.OG
=
Hướng dẫn chứng minh:
1). Ta đã chứng minh được
AH 2.OM
=
(đã
ch
ứng minh ở tính chất 2)
+ Ta có :
OA OB OC OA 2.OM OA AH OH
+ + = + = + =
2). Do G là trọng tâm
ABC
∆
OA OB OC 3.OG
⇒ + + =
OA 2.OM 3.OG
OA AH 3.OG
OH 3.OG
⇒ + =
⇒ + =
⇒ =
V
ậy 3 điểm O, G, H thẳng hàng
I
H'
C
B
A
O
H
O
A'
C
M
B
A
H
G
CHINH PH
ỤC
HÌNH H
ỌC TỌA ĐỘ PHẲNG
Trang
3
Nguồn: http://www.toanmath.com/
Tính chất 6: Cho
ABC
∆
nội tiếp đường tròn (O). Gọi D, E theo thứ tự là chân các đường cao từ
A, B. Các điểm M, N theo thứ tự là trung điểm BC và AB.
⇒
tứ giác MEND nội tiếp.
Hướng dẫn chứng minh:
+ Ta có D là trung điểm HH’ (tính chất 1), M
là trung điểm HA’ (do HCA’B là hình bình
hành - tính chất 2). Như vậy ta có phép vị tự :
1
H;
2
(A ') M
V :
(H ') D
=
=
+ Mà 2 điểm A’, H’ thuộc đường tròn ngoại
tiếp
ABC
∆
⇒
2 điểm M, D thuộc đường
tròn (C’) là ảnh của đường tròn (C) tâm O
qua phép v
ị tự
1
H;
2
V
(1)
+ Chứng minh tương tự ta cũng có 2 điểm N,
E thuộc đường tròn (C’) là ảnh của đường
tròn (C) tâm O qua phép vị tự
1
H;
2
V
(2)
+ Từ (1) và (2)
⇒
4 điểm D, M, E, N thuộc
đường tròn (C’).
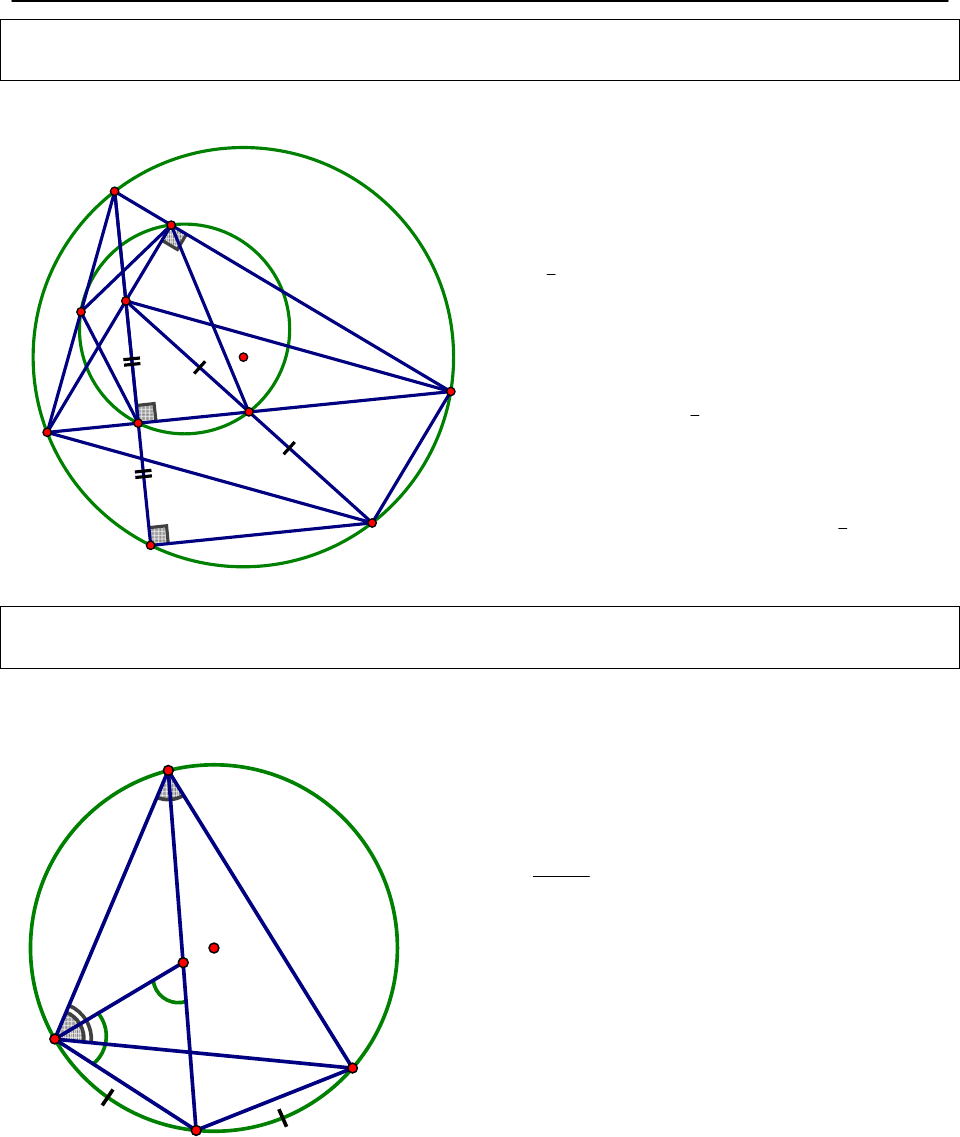
Tính chất 7: Cho
ABC
∆
, gọi O và I lần lượt là tâm đường tròn ngoại tiếp, tâm đường tròn nội
tiếp
ABC
∆
, AI cắt đường tròn (O) tại D
DB DI DC
⇒ = =
Hướng dẫn chứng minh:
+ Ta có
1
1 1
I A B
= +
ɵ
(do
1
I
là góc ngoài
ABI
∆
)
+ Mà
1 2
B B
=
(Do BI là phân giác
ABC
∆
),
1 2
A A
=
(Do AI là phân giác
ABC
∆
), mà
2 3
sdBC
A B
2
= =
1 2 3
I B B IBD IBD
⇒ = + = ⇒ ∆ cân
tại D
DI DB
⇒ =
(1)
+ Ta lại có
1 2
A A
=
BD DC BD DC
⇒ = ⇒ = (2)
+ Từ (1) và (2)
DB DI DC
⇒ = =
N
E
D
H'
O
A'
C
M
B
A
H
1
3
2
1
21
I
O
C
D
B
A
Chia sẻ bởi:
Trịnh Thị Thanh
Trịnh Thị Thanh
Liên kết tải về
14 tính chất thường gặp trong hình học phẳng
1.010,6 KB
Tải về
Có thể bạn quan tâm
-
Nghị luận về câu nói Trong rừng có rất nhiều lối đi, ta chọn lối đi chưa có dấu chân người
-
Cách phân biệt Oxit axit và Oxit bazơ
-
Văn mẫu lớp 12: Nghị luận về vấn đề ô nhiễm không khí hiện nay (Dàn ý + 6 Mẫu)
-
Tổng hợp công thức Hóa học lớp 12 - Các công thức Hóa học 12
-
Điểm chuẩn lớp 10 năm 2024 Thanh Hóa
-
Báo cáo thu, nộp Đảng phí - Mẫu báo cáo thu, nộp Đảng phí mới nhất
-
Bài thu hoạch bồi dưỡng thường xuyên Giáo viên phổ thông 2024
-
Bài tập cuối khóa Mô đun 9 THCS (9 môn)
-
Tác phẩm Cây tre Việt Nam - Tác giả Thép Mới
-
Đề Tiếng Anh chuyên ngành Ngân hàng
Xác thực tài khoản!
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:
Số điện thoại chưa đúng định dạng!
Sắp xếp theo
Mới nhất trong tuần
Đóng
Chỉ thành viên Download Pro tải được nội dung này!
Download Pro - Tải nhanh, website không quảng cáo!
Tìm hiểu thêm