Phương pháp xử lí bài toán hình học tọa độ phẳng Tài liệu ôn tập môn Toán lớp 10
Eballsviet.com xin giới thiệu đến các bạn tài liệu Phương pháp xử lí bài toán hình học tọa độ phẳng được chúng tôi đăng tải ngay sau đây.
Đây là tài liệu hữu ích hướng dẫn phương pháp tư duy xử lý bài toán hình học tọa độ phẳng Oxy khó. Hy vọng với tài liệu này các bạn học sinh lớp 10 có thêm nhiều tài liệu tham khảo, củng cố kiến thức để đạt kết quả cao trong các bài kiểm tra, bài thi sắp tới. Mời các bạn cùng theo dõi tài liệu tại đây.
Kĩ thuật xử lí hình học tọa độ phẳng
2 | K Ỹ T H U Ậ T G I Ả I T Í C H P H Ẳ N G – Đ O À N T R Í D Ũ N G : 0 9 0 2 9 2 0 3 8 9
PHẦN I: PHƯƠNG PHÁP GÁN ĐỘ DÀI
Mục tiêu của phương pháp gán độ dài là xây dựng mối liên hệ
giữa những cái đã có và những cái chưa có.
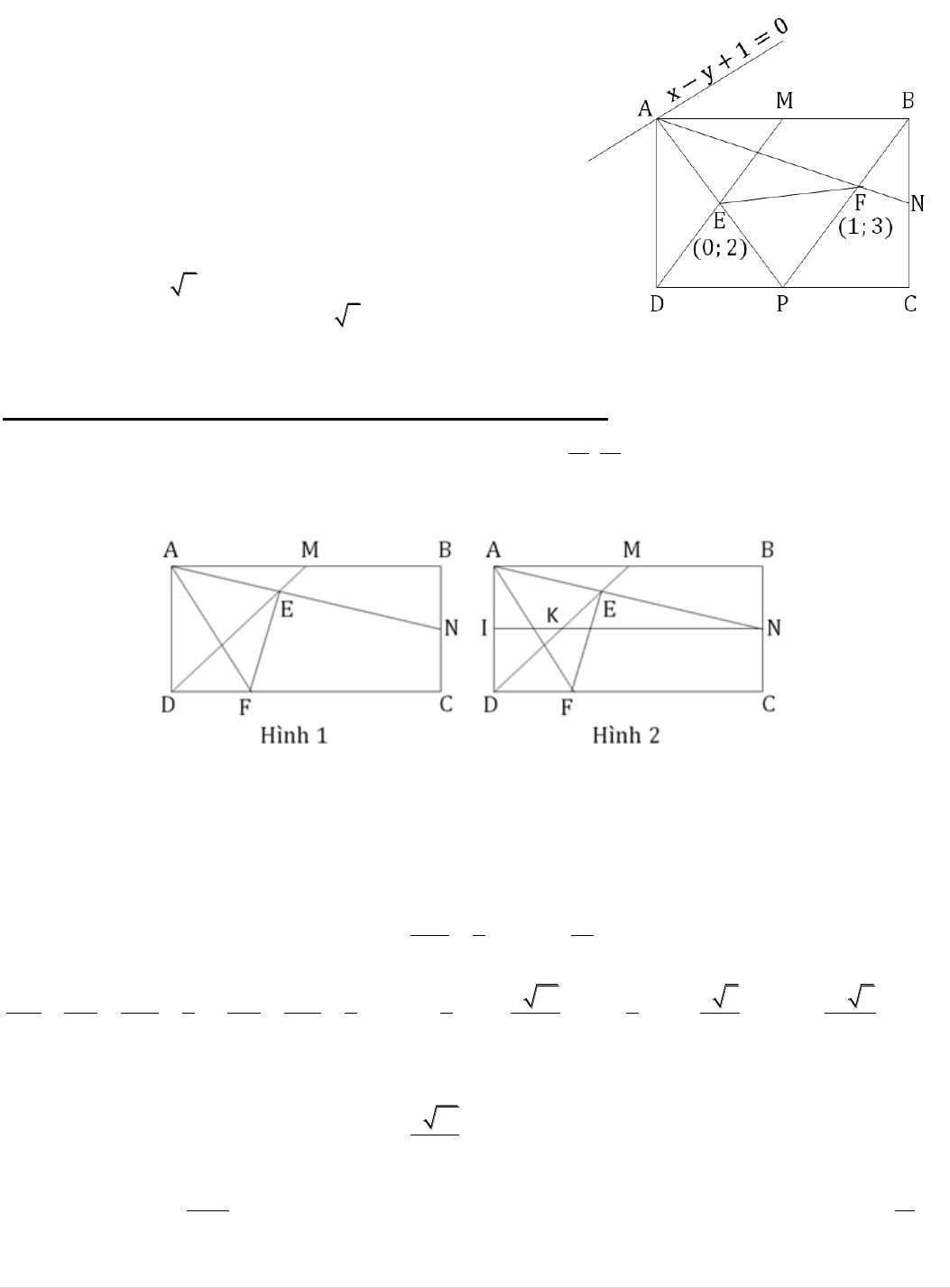
Chẳng hạn như trong hình vẽ bên thì chúng ta thấy rằng cái đã
có là độ dài EF còn cái chưa có là độ dài EA. Nếu ta tính được
độ dài EA thì vấn đề đã trở nên đơn giản hơn. Tuy nhiên thực tế
cái khó nhất chính là ở chỗ này.
Để tính EA thì ta không nên suy nghĩ quá đơn giản là đi tính độ
dài một cách trực tiếp. Thực tế đã là hình học thì không thể cứ
tính trực tiếp mà ra được. Ta sẽ tính EA thông qua các bước sau:
Bước 1: Đặt một độ dài của hình vẽ là a (có thể là cạnh
hình vuông, cạnh hình chữ nhật, chẳng hạn đặt AB = a).
Bước 2: Tính độ dài EA và EF theo a (chẳng hạn EA =
2a, EF = a
2
)
Bước 3: Độ dài EF thực tế là
2
như vậy a = 1, do đó độ
dài EA = 2. Từ đây thì việc tìm ra A là quá đơn giản.
VẤN ĐỀ 1: GÁN MỘT ĐỘ DÀI BẰNG TÍNH CHẤT HÌNH VẼ: Hình chữ nhật ABCD có AB = 2AD và
A
1;3
. M và N là trung điểm của AB và BC. DM cắt AN tại E
13 13
;
55
. F là điểm nằm trên đoạn thẳng CD
sao cho 10DF = 3CD. Biết rằng điểm F nằm trên đường thẳng
:11 5 16 0d x y
. Xác định tọa độ đỉnh F.
Bài toán này có một mối quan hệ rất dễ nhìn thấy đó chính là mối quan hệ vuông góc giữa A, E và F. Trong
bài toán này tôi sẽ sử dụng kỹ thuật gán độ dài để chứng minh mối quan hệ đó bằng Pithagore.
Các vấn đề tìm nốt ra các điểm còn lại để hoàn thiện bài toán, học sinh tự xử lý nốt.
Đặt độ dài cạnh AD = a, AB = 2a, gọi I là trung điểm của AD và K là trung điểm của DM. Ta dễ dàng thấy
được các điểm I, K, N thẳng hàng. Ta có
a 3a
2 2 2
AM
IK KN
. Mặt khác theo định lý Thales ta có:
2 2 2 a 17 2 a 2 4a 2
,
3 5 5 5 5 5 5
ME AE AM AE ME
AE AN ME MK DE
EK EN NK AN MK
Ta dễ dàng nhận thấy
= 45
0
nên áp dụng định lý hàm số cos cho tam giác DEF ta được:
2 2 2 0
a 17
2 . .cos45
5
FE DE DF DE DF FE
. Xét tam giác ADF ta được:
2
2 2 2 2 2
34a
25
FA AD DF AE FE
. Vậy tam giác AEF vuông cân tại E. Do đó ta tìm được điểm F
11
;1
5
3 | K Ỹ T H U Ậ T G I Ả I T Í C H P H Ẳ N G – Đ O À N T R Í D Ũ N G : 0 9 0 2 9 2 0 3 8 9
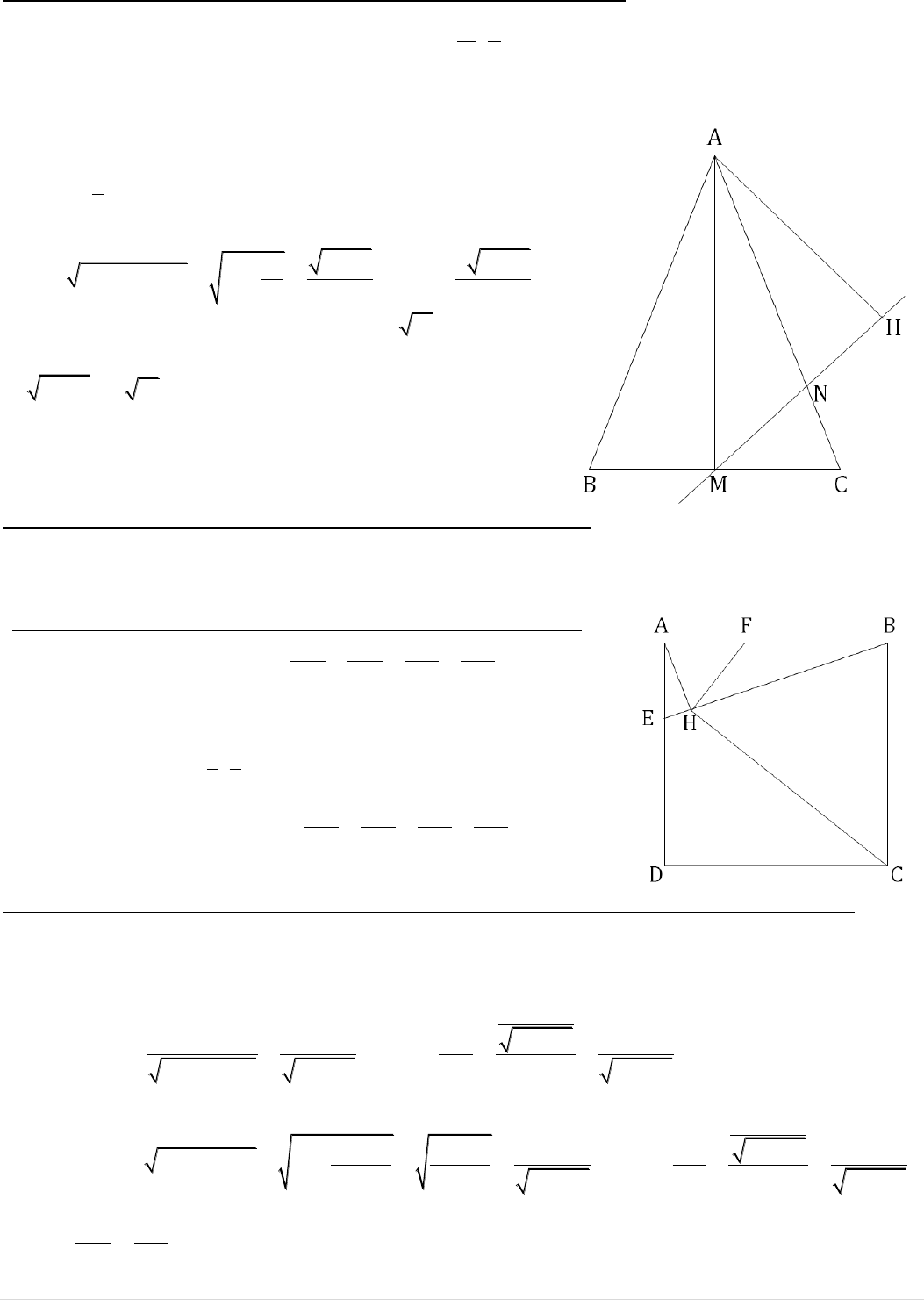
VẤN ĐỀ 2: GÁN MỘT ĐỘ DÀI DỰA VÀO THÔNG SỐ ĐẦU BÀI: Tam giác ABC cân tại A
2;4
có
diện tích bằng 3. Gọi M là trung điểm của BC và N
11 7
;
44
là điểm nằm trên cạnh AC sao cho AC = 4CN.
Biết rằng đường thẳng MN có phương trình
10xy
. Xác định tọa độ đỉnh M.
Nhìn qua thì bài toán này không thể gán được độ dài, tuy nhiên
nếu để ý kỹ thì từ chi tiết diện tích bằng 3, ta đặt AM = a, ta sẽ
có BC =
6
a
. Do vậy mục tiêu của chúng ta trong bài toán này là
tính được AN theo a. Ta có:
44
2 2 2
2
9 a 9 3 a 9
a
a a 4a
AC AM MC AN
Mặt khác vì A
2;4
và N
11 7
;
44
nên
3 10
4
AN
. Như vậy:
4
3 a 9 3 10
a 1 a 3
4a 4
AM AM
Từ đây việc tìm điểm M đã trở nên đơn giản hơn rất nhiều. Học
sinh tự giải quyết nốt bài toán đến khi kết thúc.
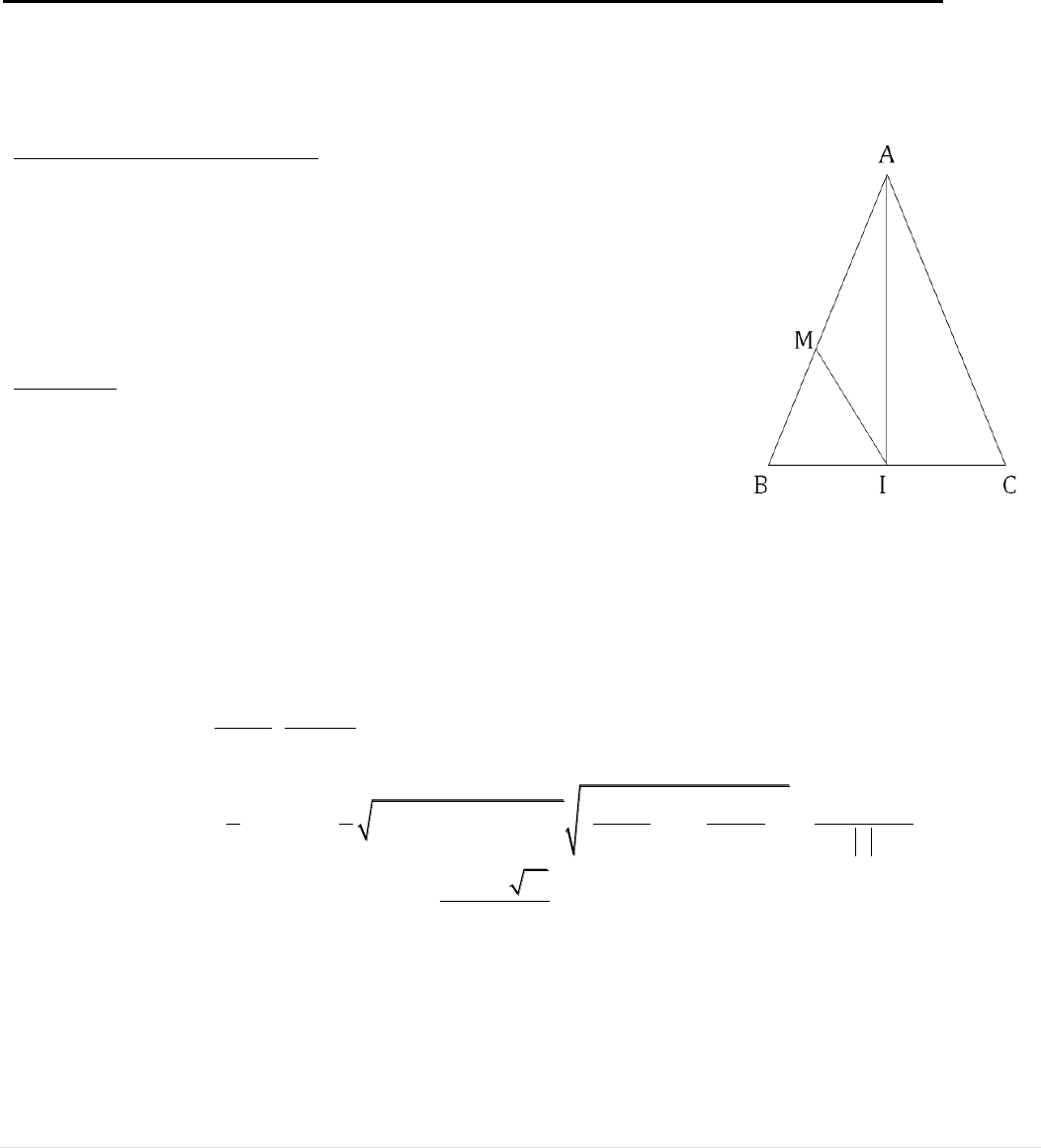
VẤN ĐỀ 3: GÁN HAI ĐỘ DÀI CHO HAI CẠNH KHÁC NHAU: Hình vuông ABCD. Trên các cạnh AD,
AB lần lượt lấy E và F sao cho AE = AF. Gọi H là hình chiếu vuông góc của A trên BE. Tìm tọa độ đỉnh C
biết C thuộc đường thẳng
2 1 0xy
và hai điểm F
2;0
, H
1; 1
.
Trước hết ta tìm hiểu về cách chứng minh bằng hình học thuần túy:
Ta có
và
AH AH BH BH
FA AE BA BC
nên ta có hai
tam giác đồng dạng HAF và HBC nên
.
Vì
+
= 90
0
nên
+
= 90
0
hay CH HF do đó ta tìm
được tọa độ điểm C
11
;
33
.
Tuy nhiên vấn đề khó nhất là tỷ số
AH AH BH BH
FA AE BA BC
làm thế nào
xử lý tốt được.
Gán độ dài có giải quyết được tỷ số trên không khi mà E và F đều là hai điểm bất kỳ trên AD và AB?
Câu trả lời là CÓ. Nếu ta đặt AB = a, AE = AF = b thì khi đó với mục tiêu hai tam giác HAF và HBC đồng
dạng, ta tập trung vào độ dài các cạnh AH, FA, BH, BC.
Tính AH:
2 2 2 2
.AE AB ab
AH
AE AB a b
. Do đó:
22
22
ab
AH a
ab
FA b
ab
Tính BH:
2 2 4 2
2 2 2
2 2 2 2
22
a b a a
BH AB AH a
a b a b
ab
. Do đó:
2
22
22
a
BH a
ab
BC a
ab
Khi đó:
AH
FA
=
BH
BC
nên các tam giác HAF và HBC đồng dạng. Do đó ta tìm được C.
4 | K Ỹ T H U Ậ T G I Ả I T Í C H P H Ẳ N G – Đ O À N T R Í D Ũ N G : 0 9 0 2 9 2 0 3 8 9
PHẦN II: PHƯƠNG PHÁP GỌI ẨN TRÊN ĐƯỜNG THẲNG
Giống như phương pháp bình phương trong phương trình – hệ phương trình, phương pháp gọi ẩn trên đường
thẳng là phương pháp đơn giản nhất, dễ hiểu dễ làm, chỉ có tính là hơi khó, đòi hỏi học sinh phải có kỹ năng
tính toán tốt và tuân thủ theo các nguyên tắc như sau:
Mỗi một điểm trên đường thẳng có thể gọi tham số trên đường thẳng đó.
Hai điểm khác nhau phải gọi hai tham số khác nhau.
Thường chỉ sử dụng khi bài toán xuất hiện hai đường thẳng trở lên.
Gọi tối đa 2 ẩn, hạn chế tối đa gọi đến ẩn thứ 3.
Có bao nhiêu ẩn phải đưa ra bấy nhiêu phương trình.
VẤN ĐỀ 1: GỌI MỘT ẨN VÀ TÍNH TỌA ĐỘ CÁC ẨN KHÁC BẰNG CÁCH KÉO THEO: Tam giác
ABC cân tại A có phương trình đường thẳng chứa cạnh BC là:
2 3 0xy
và I
2; 1
là trung điểm của
BC. Điểm M
4;1
nằm trên cạnh AB và tam giác ABC có diện tích bằng 90. Tìm tọa độ các đỉnh của tam giác
ABC biết rằng điểm B có hoành độ lớn hơn 3.
Thiết lập mục tiêu cho bài toán:
Bước 1: Gọi tọa độ của B tham số b trên đường thẳng BC.
Bước 2: Tìm tọa độ của C theo tham số b.
Bước 3: Từ B và M viết phương trình BM theo tham số b.
Bước 4: Viết được phương trình AI qua I vuông góc với BC.
Bước 5: Tìm được tọa độ A theo tham số b là giao của BM và AI.
Bước 6: Giải phương trình diện tích tam giác ABC bằng 90 ra b.
Bước 7: Kết luận.
Thực hiện:
Bước 1: Gọi B
;2 3bb
trên đường thẳng BC.
Bước 2: I trung điểm BC:
24
2 5 2
C I B
C I B
x x x b
y y y b
C
4 , 5 2bb
Bước 3: Từ B và M đã có ta viết phương trình đường thẳng BM:
2 2 4 4 1 0b x b y
Bước 4: Đường thẳng qua I và vuông góc với BC là AI:
2 4 0xy
Bước 5: A là giao của BM và AI nên tọa độ A là nghiệm của hệ:
2 2 4 4 1 0
2 4 0
b x b y
xy
do đó
ta tìm được tọa độ A
2 8 3 4
;
bb
bb
.
Bước 6: Ta có
1
2
ABC
S
AI.BC =
2
22
22
10 2
1 4 8 2 4
2 4 4 8
2
b
bb
bb
b b b
= 90. Do đó
giải phương trình trên ta được
13 3 17
1, 4,
2
b b b
.
Bước 7: Do điểm B có hoành độ lớn hơn 3 nên ta tìm được A
4; 4
, B
4;11
, C
8; 13
.
Chia sẻ bởi: 
Trịnh Thị Thanh
Trịnh Thị Thanh Liên kết tải về
Link Download chính thức:
Phương pháp xử lí bài toán hình học tọa độ phẳng Download
Có thể bạn quan tâm
-
Mẫu 09/ĐK: Đơn đăng ký biến động đất đai
-
Tranh tô màu Pikachu - Bộ tranh tô màu Pikachu đẹp
-
Giáo án Toán lớp 1 (Sách mới) - Giáo án Toán lớp 1 (trọn bộ 5 sách)
-
Tuyển tập đề thi học sinh giỏi môn Toán lớp 3
-
Thuyết minh về Thành Cổ Loa (2 Dàn ý + 5 mẫu)
-
Bộ tranh tô màu chủ đề gia đình cho bé
-
Văn mẫu lớp 10: Phân tích tác phẩm Hiền tài là nguyên khí của quốc gia (2 Dàn ý + 10 Mẫu)
-
Những vần thơ hay - Tuyển tập những bài thơ hay
-
Văn mẫu lớp 9: Nghị luận về hiện tượng học tủ, học vẹt
-
File luyện viết chữ in hoa - Mẫu chữ hoa cho học sinh Tiểu học
Sắp xếp theo
