Phương pháp tọa độ hóa bài toán hình không gian Tài liệu ôn tập môn Toán lớp 12
Phương pháp tọa độ hóa bài toán hình không gian là tài liệu hữu ích gồm 24 trang giới thiệu phương pháp tọa độ hóa bài toán hình không gian và các ví dụ minh họa có lời giải chi tiết kèm theo.
Hy vọng với tài liệu này các bạn học sinh lớp 12 có thêm nhiều tài liệu tham khảo, củng cố kiến thức để đạt được kết quả cao trong các bài kiểm tra, bài thi THPT Quốc gia sắp tới. Đồng thời giúp các thầy cô giáo có thêm nhiều tài liệu giảng dạy. Mời các bạn cùng theo dõi bài viết dưới đây.
Phương pháp tọa độ hóa bài toán hình không gian
Trung tâm SEG.154-Huỳnh Mẫn Đạt-p3-q5-TP.HCM
ThS. Trần Duy Thúc . Sđt: 0979.60.70.89 Nơi nào có ý chí,nơi đó có con đường! 1
PHƯƠNG PHÁP TỌA ĐỘ HÓA BÀI TOÁN HÌNH KHÔNG GIAN
I. Lý thuyết cần nhớ
1. Cách chọn gốc tọa độ
Ưu điểm:Khi ta chọn được tọa độ các điểm thì chỉ cần áp dụng các kiến thức hình giải tích như khoảng
cách, góc, chứng minh vuông góc…Tuy nhiên, với một số Em học sinh thì việc tính được tọa độ là vấn đề?
Về nguyên tắc thì Em có thể chọn gốc tọa độ nằm bất cứ chổ nào, nhưng chọn chổ nào thì việc tính tọa độ
là thuận lợi nhất? Sai lầm của không ít người dẫn đến việc tính tọa độ các điểm phức tạp là cứ thấy chân
đường cao của hình chóp là chọn làm gốc tọa độ. Trong một số trường hợp Em chọn như vậy sẽ dẫn đến
việc tính tọa độ khó khăn và dễ bị chán nản. Để thuận lợi cho việc tính tọa độ Em nhớ nguyên tắc sau đây.
2.Nguyên tắc chọn gốc tọa độ
+ Vẽ hình thực của đa giác đáy ra bên cạnh.
+ Ưu tiên chọn gốc tọa độ là góc vuông của đa giác đáy chứ không phải là ưu tiên chân đường cao. Tất
nhiên nếu chân đường cao mà trùng gốc vuông ở đáy thì ta chọn gốc tọa ngay điểm đó luôn là tốt.
+ Nhìn vào hình thực này để tính tọa độ các điểm trong mặt phẳng đáy trước. Sau đó tính các điểm phát
sinh và đỉnh.
+ Cứ quan tâm vào việc chọn trục
;Ox Oy
ở đáy, sau đó gắn trục
Oz
vào là xong.
Chẳng hạn ta có 1 số trường hợp chọn gốc tọa độ như sau:
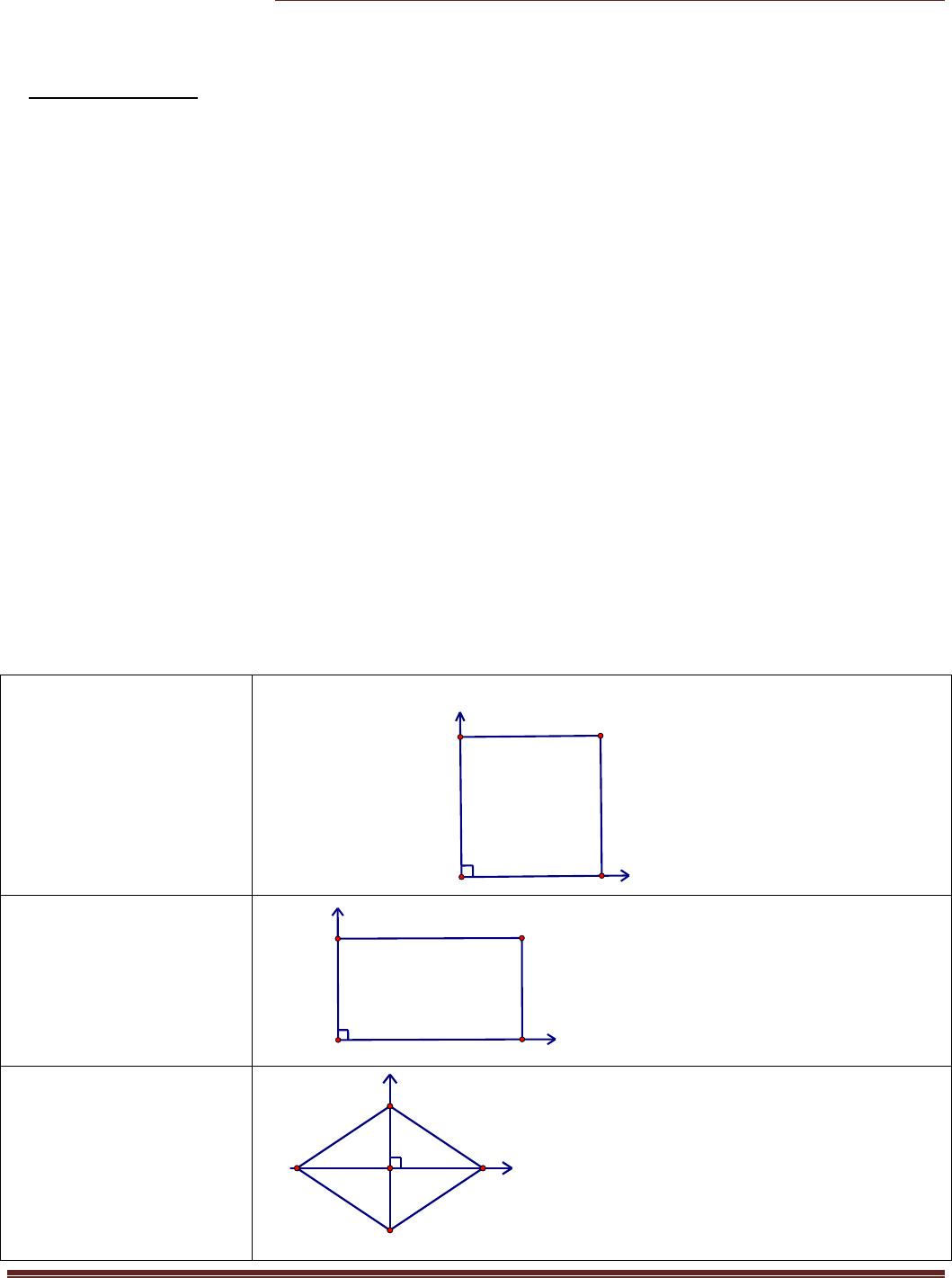
1. Đáy là hình vuông
Chọn tọa độ tại đỉnh nào cũng được.
2. Đáy là hình chữ nhật
3. Hình thoi
Chọn góc tọa độ tại tâm I của hình thoi.
y
x
D
A
B
C
x
y
D
B
C
A
x
y
B
C
I
A
D
Trung tâm SEG.154-Huỳnh Mẫn Đạt-p3-q5-TP.HCM
ThS. Trần Duy Thúc . Sđt: 0979.60.70.89 Nơi nào có ý chí,nơi đó có con đường! 2
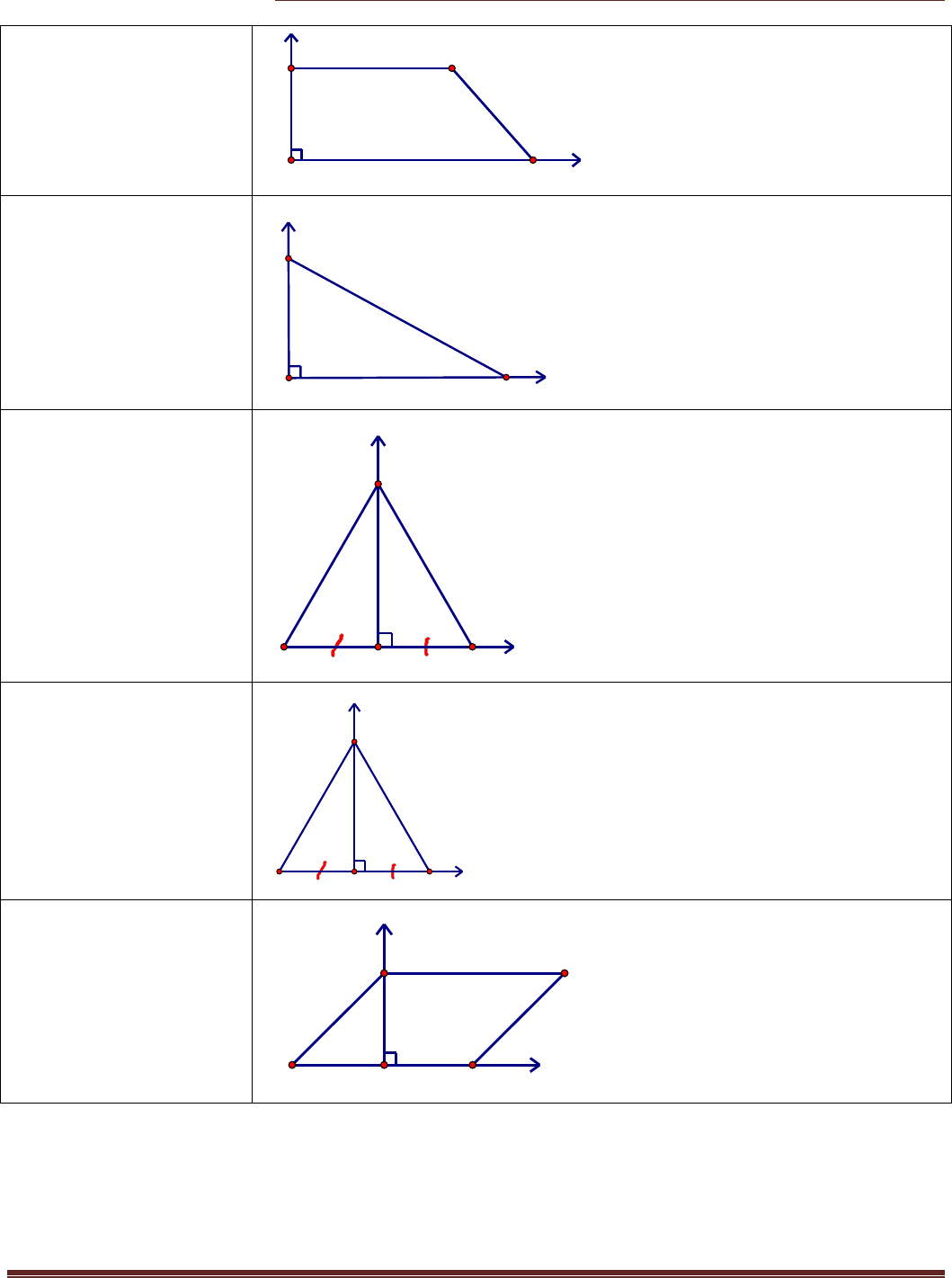
4. Hình thang vuông
Chọn góc tọa độ ngay gốc vuông.
5. Tam giác vuông
Chọn góc tọa độ ngay gốc vuông.
6. Tam giác đều
Góc tọa độ là trung điểm H một cạnh của tam
giác đều.
7. Tam giác cân
Góc tọa độ là trung điểm H của cạnh đáy.
8. Hình bình hành
Kẻ thêm đường cao BH và góc tọa độ
là H.
y
x
B
C
A
D
x
y
C
B
A
y
y
H
B
A
C
y
y
H
B
A
C
y
x
H
D
B
C
A
Trung tâm SEG.154-Huỳnh Mẫn Đạt-p3-q5-TP.HCM
ThS. Trần Duy Thúc . Sđt: 0979.60.70.89 Nơi nào có ý chí,nơi đó có con đường! 3
II. Một số yêu cầu thường gặp
1. Chứng minh quan hệ song song,vuông góc
2. Khoảng cách từ một điểm đến một mặt phẳng
Cho điểm
0 0 0
;;M x y z
và mặt phẳng
:0 P Ax By Cz D
. Khi đó:
0 0 0
2 2 2
;
Ax By Cz D
d M P
A B C
.
3. Khoảng cách giữa hai đường thẳng
Cho hai đường thẳng điểm
12
;dd
có hai vectơ chỉ phương lần lượt là
;ab
. Các điểm A và B lần lượt thuộc
12
;dd
.Khi đó:
12
;.
;d
;
a b AB
dd
ab
.
4. Góc giữa hai đường thẳng
Cho hai đường thẳng điểm
12
;dd
có hai vectơ chỉ phương lần lượt là
;ab
.Khi đó:
12
.
cos ;d
.
ab
d
ab
.
III. Bài tập mẫu
Chú ý: Các ví dụ ở đây, Thầy chỉ sử dụng phương pháp tọa độ để giúp các Em giải quyết triệt để ý sau của
bài toán hình không gian thôi. Ý đầu tiên vẩn tính bình thường theo hình không gian thuần túy nhé!
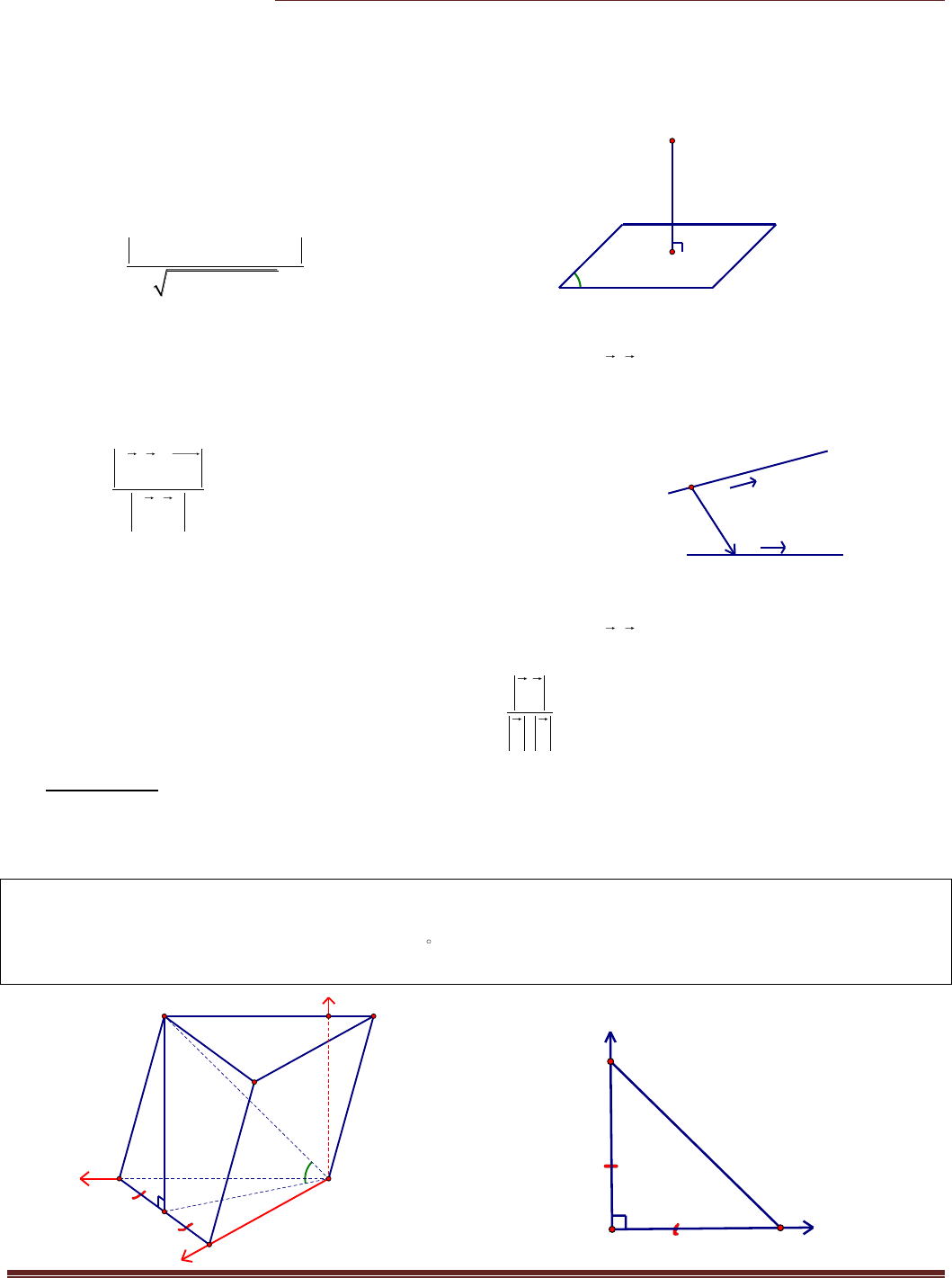
Ví dụ 1.(Trích đề THPT Quốc Gia -2016) Cho hình lăng trụ ABC.A’B’C’ có đáy là tam giác vuông cân
tại B; AC= 2a. Hình chiếu vuông góc của A’ trên mặt phẳng (ABC) là trung điểm của cạnh AC; đường
thẳng A’B tạo với mặt phẳng (ABC) một góc
45
. Tính theo a thể tích của khối lăng trụ ABC.A’B’C’ và
chứng minhg A’B vuông góc B’C.
Giải
P
d
(
M;
(
P
))
M
d1
d2
a
b
B
A
y
x
2a
A
B
C
45
x
y
z
B'
C'
H
A
B
C
A'
Chia sẻ bởi: 
Trịnh Thị Thanh
Trịnh Thị Thanh Liên kết tải về
Link Download chính thức:
Phương pháp tọa độ hóa bài toán hình không gian Download
Có thể bạn quan tâm
-
Mẫu 09/ĐK: Đơn đăng ký biến động đất đai
-
Tranh tô màu Pikachu - Bộ tranh tô màu Pikachu đẹp
-
Giáo án Toán lớp 1 (Sách mới) - Giáo án Toán lớp 1 (trọn bộ 5 sách)
-
Tuyển tập đề thi học sinh giỏi môn Toán lớp 3
-
Thuyết minh về Thành Cổ Loa (2 Dàn ý + 5 mẫu)
-
Bộ tranh tô màu chủ đề gia đình cho bé
-
Văn mẫu lớp 10: Phân tích tác phẩm Hiền tài là nguyên khí của quốc gia (2 Dàn ý + 10 Mẫu)
-
Những vần thơ hay - Tuyển tập những bài thơ hay
-
Văn mẫu lớp 9: Nghị luận về hiện tượng học tủ, học vẹt
-
File luyện viết chữ in hoa - Mẫu chữ hoa cho học sinh Tiểu học
Sắp xếp theo
