Phân dạng và phương pháp giải trắc nghiệm chuyên đề hàm số Tài liệu luyện thi THPT Quốc gia 2019
Phân dạng và phương pháp giải trắc nghiệm chuyên đề hàm số là tài liệu cực kì hữu ích mà Eballsviet.com muốn giới thiệu đến quý thầy cô cùng các bạn học sinh lớp 12 cùng tham khảo.
Phân dạng và phương pháp giải trắc nghiệm chuyên đề hàm số là tài liệu gồm 96 trang tuyển tập bài tập trắc nghiệm về cực trị của hàm số, nội dung gồm 4 phần: Biện luận nghiệm bằng đồ thị; Biến đổi đồ thị trị tuyệt đối; Tổng ôn; Phép tịnh tiến. Sau đây là nội dung chi tiết, mời các bạn cùng tham khảo và tải tại đây.
Phương pháp giải trắc nghiệm chuyên đề hàm số
1
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIỆN LUẬN
2017
◙ Lý Thuyết : Ta xét bài toán sau đây :
Vẽ đồ thị (C) của hàm số
()y f x
sau đó biện luận
theo tham số m số nghiệm của phương trình :
( ; m) 0hx
(♥)
☻ Ta đưa (♥) về dạng
Trong đó
()fm
là biểu thức theo m, không chứa x
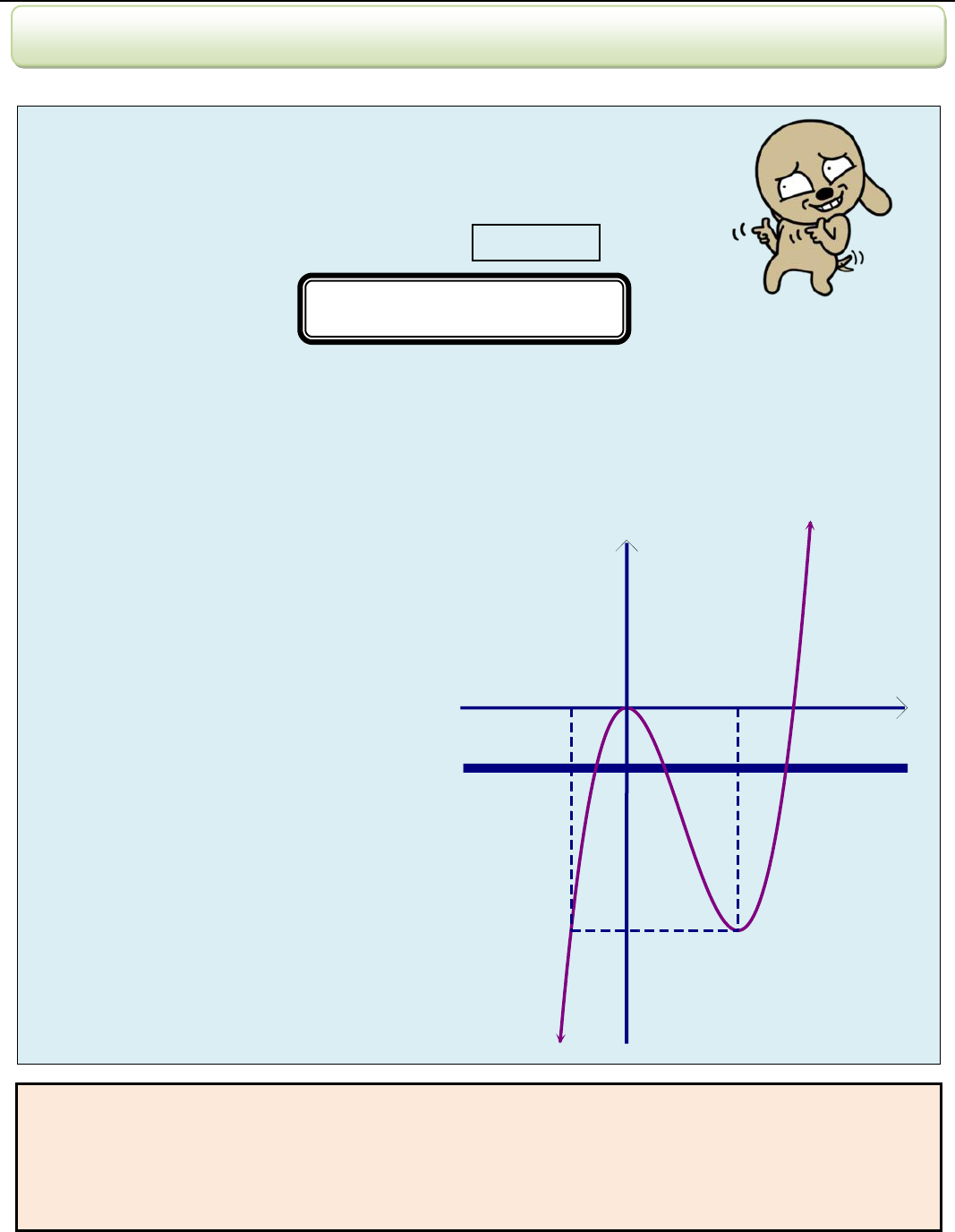
Số nghiệm của (♥) chính là số giao điểm của (C) và đường thẳng (D)
()y f m
mà ta nhìn thấy
qua đồ thị ((D) ............................. Ox )
VD như hình bên, ta thấy (♥) có :
☻ 3 nghiệm khi ............................................
☻ 2 nghiệm khi .......................
hoặc ...............................
☻ 1 nghiệm khi .......................
hoặc ...............................
Ví dụ 01 : Cho hàm số
32
34y x x
(có đồ thị là (C))
a/ Khảo sát và vẽ đồ thị hàm số.
b/ Biện luận theo
m
số nghiệm của phương trình
32
30x x m
.
PHẦN 8 : BIỆN LUẬN NGHIỆM BẰNG ĐỒ THỊ
_
x
_
,
_
_
y
_ =
_
f
_
(
_
m
_
)
_
y
_
-4
_
3
_
2
_
-
1
_
O
2
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIỆN LUẬN
2017
a/ ► Tập xác định
D
.
► Đạo hàm
2
' 3 6 3 2y x x x x
;
0
'0
2
x
y
x
.
► Hàm số đồng biến trên khoảng
2;0
;
nghịch biến trên các khoảng
;2
và
0;
.
► Hàm số đạt cực đại tại
0x
,
CD
4y
; đạt cực tiểu tại
2x
,
CT
0y
.
► Giới hạn tại vô cực
lim
x
y
; và
lim
x
y
.
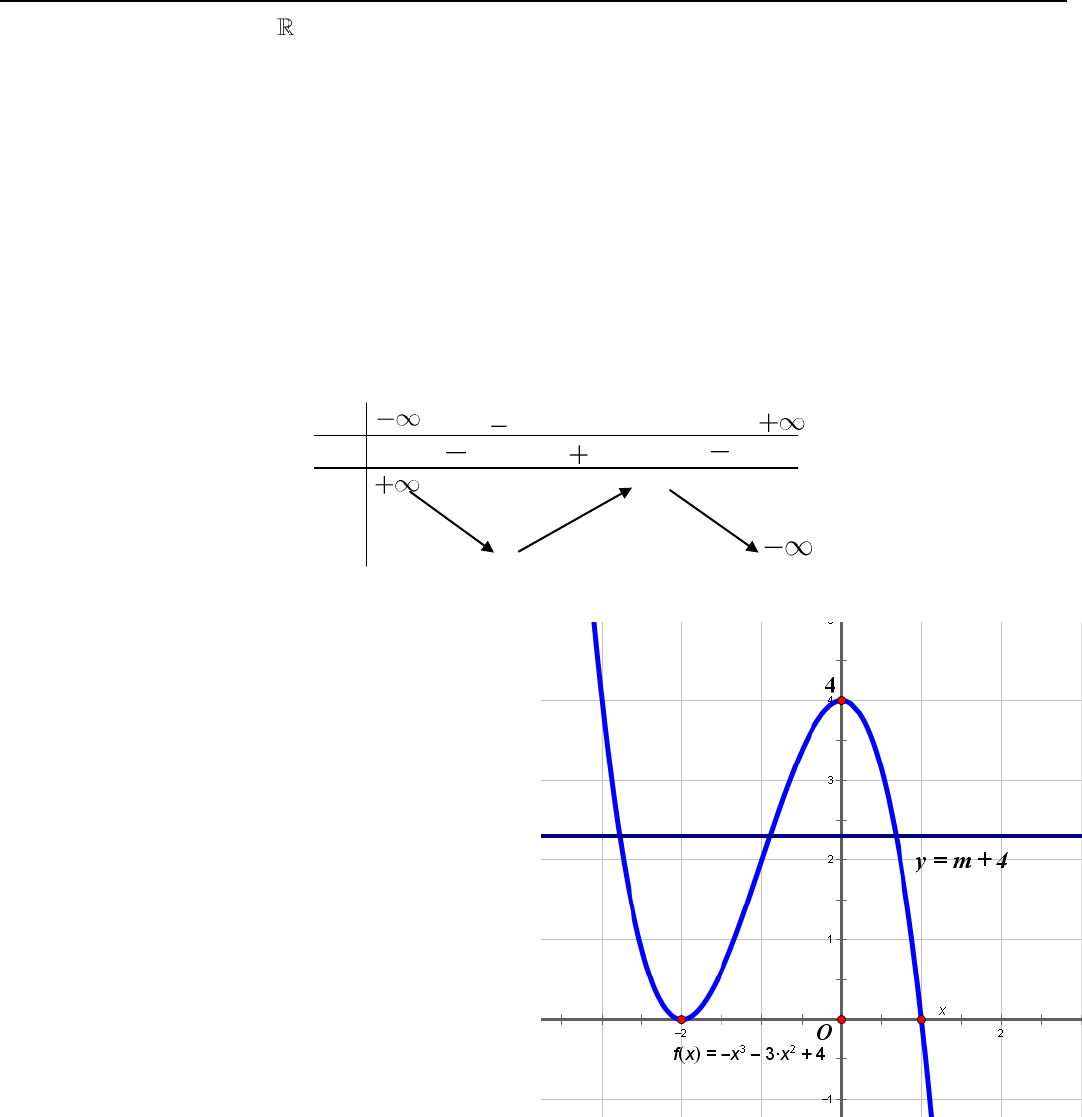
► Bảng biến thiên
► Đồ thị hàm số đi qua các điểm
3;4
,
1;0
.
b/ Ta có
32
30x x m
32
3 4 4 *x x m
.
Phương trình
*
là phương trình hoành độ
giao điểm của đồ thị và đường thẳng
4ym
.Do đó số nghiệm của phương trình
*
là số giao điểm của đồ thị và đường thẳng
d:
4ym
. (d cùng phương Ox)
Dựa vào đồ thị, ta có
♥ Với
4 4 0
4 0 4
mm
mm
: Phương trình có
duy nhất
1
nghiệm.
♥ Với
4 4 0
4 0 4
mm
mm
: Phương trình có
2
nghiệm.
♥ Với
0 4 4 4 0mm
: Phương trình có
3
nghiệm.
y
x
'y
2
4
0
0
0
0
3
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIỆN LUẬN
2017
0
-4
-∞
+∞
m
☻Toán nếu trắc nghiệm thì đề sẽ bắt chúng ta “suy luận và hiểu” nhiều hơn là phương pháp
“Casio thần chưởng”
☻Vậy phải làm sao ???
☻Thật ra thì “bảng biến thiên đã nói lên tất cả”rồi
Chúng ta bắt tay vào làm !!! Ở đây thầy không dùng bảng biến thiên cũ (nếu dùng vẫn
được) để cho các em biết là đưa về hàm nào cũng được ☺
Phương trình
32
30x x m
ta viết lại
32
3m x x
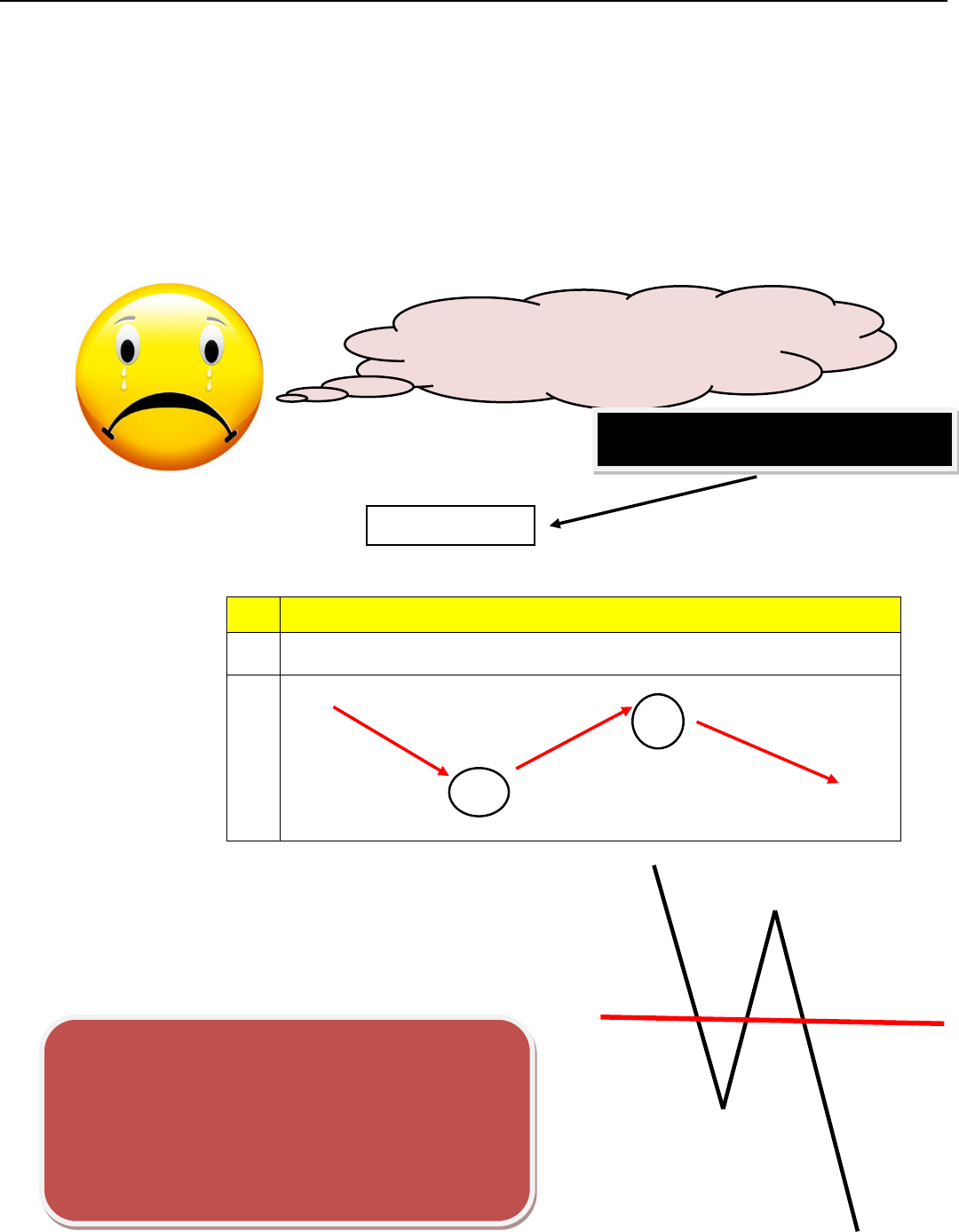
Lập BBT đi
“phác thảo” đồ thị
Từ đồ thị “phác thảo” này ta thấy rõ ràng
ở đây thầy ví dụ có 3 nghiệm !!!thì m chạy từ - 4 đến 0
x
2
0
'y
0
0
y
0
4
2 con số đáng yêu !!!
(biện luận ko cần vẽ đồ thị)
Đây không phải là công thức giải nhanh –
chỉ là hướng tư duy giúp giải bài toán
nhanh hơn cho trắc nghiệm !!
Vẽ đồ thị mất 15 phút rồi
Nhìn hàm g(x) này nè !!!
Chia sẻ bởi: 
Trịnh Thị Thanh
Trịnh Thị Thanh Liên kết tải về
Phân dạng và phương pháp giải trắc nghiệm chuyên đề hàm số 4,9 MB Tải về
Có thể bạn quan tâm
-
Soạn bài Các loài chung sống với nhau như thế nào? - Kết nối tri thức 6
-
Văn mẫu lớp 12: Dàn ý phân tích sức sống tiềm tàng của Mị (6 Mẫu + Sơ đồ tư duy)
-
Bộ đề thi học kì 2 môn Ngữ văn 7 năm 2023 - 2024 sách Chân trời sáng tạo
-
Bộ đề thi học sinh giỏi môn Ngữ văn lớp 7
-
Văn mẫu lớp 12: Nghị luận xã hội về giờ trái đất (Dàn ý + 7 Mẫu)
-
Văn mẫu lớp 12: Phân tích tình huống truyện Chiếc thuyền ngoài xa
-
Dẫn chứng về Cho và nhận - Ví dụ về Cho và Nhận trong cuộc sống
-
Soạn bài Bức tranh của em gái tôi - Cánh Diều 6
-
Bộ đề thi học kì 2 môn Ngữ văn lớp 7 năm 2023 - 2024 (Sách mới)
-
Văn mẫu lớp 12: Nghị luận xã hội Đời phải trải qua giông tố nhưng không được cúi đầu trước giông tố
Xác thực tài khoản!
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:
Số điện thoại chưa đúng định dạng!
Sắp xếp theo
