Lăng kính: Cấu tạo, công thức và Bài tập Công thức Lăng kính

Lăng kính là một khối chất trong suốt (thủy tinh, nhựa ...) thường có dạng lăng trụ tam giác. Khi sử dụng lăng kính, chùm tia sáng hẹp được chiếu truyền qua lăng kính trong một mặt phẳng vuông góc với cạnh của khối lăng trụ. Vậy công thức lăng kính như thế nào? Mời các bạn cùng theo dõi bài viết dưới đây của Eballsviet.com.

Thông qua tài liệu công thức lăng kính các bạn học sinh lớp 11 có thêm nhiều tài liệu ôn tập, nhanh chóng biết cách giải các bài tập Vật lí 11 để đạt kết quả cao trong các bài kiểm tra, bài thi học kì 2 Vật lý 11. Bên cạnh đó các bạn xem thêm công thức thấu kính, Khúc xạ ánh sáng.

I. Cấu tạo lăng kính

Lăng kính là một khối chất trong suốt (thủy tinh, nhựa ...) thường có dạng lăng trụ tam giác.

Khi sử dụng lăng kính, chùm tia sáng hẹp được chiếu truyền qua lăng kính trong một mặt phẳng vuông góc với cạnh của khối lăng trụ. Do đó, lăng kính được biểu diễn bằng tam giác tiết diện phẳng.

Các phần tử của lăng kính gồm: cạnh, đáy, hai mặt bên.

Về phương diện quang học, một lăng kính được đặc trưng bởi:

• Góc chiết quang A;
• Chiết suất n.

Ta khảo sát lăng kính đặt trong không khí.

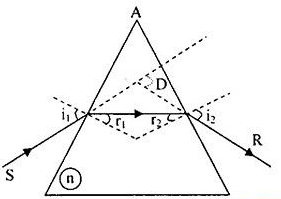
II. Đường truyền của tia sáng lăng kính

a. Tác dụng tán sắc ánh sáng trắng

Ta đã biết, ánh sáng trắng (ánh sáng mặt trời) gồm nhiều ánh sáng màu và lăng kính có tác dụng phân tích chùm sáng truyền qua nó thành nhiều chùm sáng màu khác nhau.

Đó là sự tán sắc ánh sáng bởi lăng kính do Niu - tơn khám phá ra năm 1669.

Dưới đây, ta chỉ xét sự truyền của một chùm tia sáng hẹp đơn sắc (có một màu nhất định) qua một lăng kính.

b) Đường truyền của tia sáng qua lăng kính

Khi có tia ló ra khỏi lăng kính thì tia ló bao giờ cũng lệch về đáy lăng kính so với tia tới.

Góc tạo bởi tia ló và tia tới gọi là góc lệch D của tia sáng khi truyền qua lăng kính.

III. Công thức lăng kính

∗ Công thức lăng kính đặt trong không khí:

sini₁ = nsinr₁

sini₂ = nsinr₂

A = r₁ + r₂

D = i₁ + i₂ – A

∗ Trong trường hợp góc i1 và góc chiết quang A nhỏ (<10^o) thì:

i₁ = nr₁

i₂ = nr₂

A = r₁ + r₂

D = (n - 1)A

IV. Công dụng của lăng kính

a) Máy quang phổ

Lăng kính là bộ phận chính của máy quang phổ.

Máy quang phổ phân tích ánh sáng từ nguồn phát ra thành các thành phần đơn sắc, nhờ đó xác định được cấu tạo của nguồn sáng.

b) Lăng kính phản xạ toàn phần

Lăng kính phản xạ toàn phần là lăng kính thủy tinh có tiết diện thẳng là một tam giác vuông cân.

Lăng kính phản xạ toàn phần được sử dụng để điều hỉnh đường đi của tia sáng hoặc tạo ảnh thuận chiều (ống nhòm, máy ảnh…)

V. Ví dụ tính lăng kính

Ví dụ 1: Một lăng kính thủy tinh có chiết suất n = 1,41 ≈ √2. Tiết diện thẳng là một tam giác đều ABC. Chiếu một tia sáng nằm trong mặt phẳng của tiết diện thẳng, tới AB với góc tới 450. Xác định đường truyền của tia sáng.

Bài giải:

Tại I luôn có tia khúc xạ, ta có:

Sini₁ = nsinr₁

\(\operatorname{Sin} r_{1}= \frac{\sin \mathrm{i}_{1}}{\mathrm{n}}=\frac{\sin 45^{0}}{\sqrt{2}} \Rightarrow r_{1}=30^{\circ}\)

Tại J: r₂ = 60⁰ – 30⁰ = 30⁰

Áp dụng công thức thấu kính, ta có: Sini₂ = nsinr₂ ⇒ i₂ = 45⁰

Bài 2: Một lăng kính thủy tinh P có chiết suất n = 1,5, tiết diện thẳng là một tam giác ABC vuông cân tại B. Chiếu vuông góc tới mặt AB một chùm sáng song song SI // BC.

a) Khối thủy tinh P ở trong không khí.Tính góc D làm bởi tia tới và tia ló

b) Tính lại góc D nếu khối P ở trong nước có chiết suất n’ = 1,33.

Bài giải:

a) Ta tính góc giới hạn phản xạ toàn phần của lăng kính này

sin i_gh = \(\frac{1}{n}=\frac{1}{1.5}\) ⇒ i_gh = 41,81⁰ = 42⁰

Đường truyền của tia sáng qua lăng kính như sau

Tia sáng tới vuông góc với mặt bên nên truyền thẳng vào trong lăng kính.

Góc \(\widehat{\mathrm{HIN}}\) = 45⁰ > i_gh ⇒ xảy ra phản xạ toàn phần tại I.

Góc phản xạ = góc tới ⇒ góc \(\widehat{\mathrm{JIN}}\) = góc \(\widehat{\mathrm{HIN}}\) = 45⁰

=> Góc \(\widehat{\mathrm{IJC}}\) = 45⁰

Góc lệch D = góc \(\widehat{\mathrm{SIJ}}\) =90⁰
b)

Đặt lăng kính vào nước, ta có hình vẽ

Sin i_gh = \(\frac{n'}{n}=\frac{1.33}{1.5}\) ⇒ i_gh = 63⁰. Vì góc tới i = 45⁰ < igh, nên sẽ xảy ra khúc xạ tại mặt AC.

Áp dụng công thức khúc xạ ánh sáng: n.sini = n’.sinr => 1,5.sin 45⁰ = 1,33.sinr => r = 53⁰

Góc lệch: D = |r – i| = |53 – 45| = 8⁰

VI. Bài tập lăng kính

Bài 1. Một tia sáng đi từ không kí đến gặp mặt lăng kính có góc chiết quang A = 45⁰, chiết suất n = \(\sqrt{3}\) dưới góc tới i = 60⁰. Tính góc ló ra khỏi mặt bên của lăng kính.

Bài 2. Một lăng kính có chiết suất n = \(\sqrt{2}\) có tiết diện là một tam giác ABC vuông cân tại B. Một tia sáng tới SI hợp với cạnh bên AB của lăng kính một góc 60⁰. Tính góc lệch D.

Bài 3. Một lăng kính có tiết diện thẳng là DABC, góc chiết quang A = 60⁰, chiết suất n = \(\sqrt{2}\). Chiếu một chùm tia sáng hẹp đơn sắc SI nằm trong tiết diện ABC từ đáy lên mặt AB của lăng kính với góc tới i₁và có tia ló ở mặt bên AC. Tìm góc lệch D giữa tia ló và tia tới. Biết :

a) i₁= 45⁰

b) i₁= 30⁰

Bài 4 Một lăng kính tiết diện thẳng là tam giác ABC có góc chiết quang A= 30⁰, chiếu một tia sáng đơn sắc vuông góc với mặt bên AB và tia ló khỏi mặt AC với góc lệch D = 15⁰. Tính chiết suất n của chất làm lăng kính.

Bài 5. Một lăng kính có tiết diện là một tam giác đều ABC. Một tia sáng tới SI chiếu tới mặt bên AB và vuông góc với đường cao AH của lăng kính. Chùm tia ló ra khỏi lăng kính sát với mặt AC. Tính chiết suất của lăng kính và góc lệch D.

Bài 6: Chiếu một tia sáng SI đến vuông góc với màn E tại I. Trên đường đi của tia sáng, người ta đặt đỉnh I của một lăng kính thủy tinh có góc chiết quang A = 5⁰, chiết suất n = 1,5 sao cho SI vuông góc với mặt phân giác của góc chiết quang I, tia sáng ló đến màn E tại điểm J. Tính IJ, biết rằng màn E đặt cách đỉnh I của lăng kính một khoảng 1m.

Bài 7 : Một lăng kính có tiết diện thẳng là tam giác vuông cân ABC, A=90⁰được đặt sao cho mặt huyền BC tiếp xúc với mặt nước trong chậu, nước có n=4/3.

a.Một tia sáng đơn sắc SI đến mặt bên AB theo phương nằm ngang.Chiết suất n của lăng kính và khoảng cách AI phải thỏa mãn điều kiện gì để tia sáng phản xạ toàn phần tại mặt BC ?

b.Giả sử AI thỏa mãn điều kiện tìm được, n=1,41.Hãy vẽ đường đi của tia sáng ?

Bài 8 :Một lăng kính thủy tinh có tiết diện thẳng là tam giác cân ABC đỉnh A. Một tia sáng rọi vuông góc vào mặt bên AB sau hai lần phản xạ toàn phần liên tiếp trên mặt AC và AB thì ló ra khỏi BC theo phương vuông góc BC.

a.A= ? (36⁰)

b.Tìm điều kiện chiết suất phải thỏa mãn ?(n>1,7)

Bài 9. Một lăng kính có chiét suất n= \(\sqrt{2}\) Chiếu một tia sáng đơn sắc vào mặt bên của lăng kính góc tới i = 45⁰ . tia ló ra khói lăng kính vuông góc với mặt bên thứ hai.Tìm góc chiết quang A ?

Bài 10 :Một lăng kính thuỷ tinh có chiết suất n =1,6. Chiếu một tia sáng đơn sắc theo phương vuông góc với mặt bên của lăng kính . Tia sáng phản xạ toàn phần ở mặt bên của lăng kính

Tính giá trị nhỏ nhất của góc A ?