Định luật Fa-ra-day Công thức Faraday
Định luật Faraday là gì? Công thức Faraday như thế nào? Là câu hỏi được rất nhiều bạn học sinh quan tâm. Chính vì vậy trong bài viết dưới đây Eballsviet.com trân trọng giới thiệu toàn bộ kiến thức về Faraday như: nội dung định luật, công thức kèm theo một số ví dụ minh họa. Thông qua tài liệu này các bạn có thêm nhiều tư liệu ôn tập, củng cố kiến thức để biết cách giải các bài tập Vật lí 11.
Định luật cảm ứng Faraday là định luật cơ bản trong điện từ, cho biết từ trường tương tác với một mạch điện để tạo ra sức điện động - một hiện tượng gọi là cảm ứng điện từ. Đó là nguyên lý hoạt động cơ bản của máy biến áp, cuộn cảm, các loại động cơ điện, máy phát điện và nam châm điện. Bên cạnh đó các bạn xem thêm công thức tính nhiệt lượng tỏa ra.
Định luật Faraday: Công thức và bài tập
1. Phát biểu định luật Faraday
Khối lượng chất giải phóng ở mỗi điện cực tỉ lệ với điện lượng đi qua dung dịch và đương lượng của chất.
2. Công thức Faraday
![]() \(m = \frac{{A.I.t}}{{n.F}}\)
\(m = \frac{{A.I.t}}{{n.F}}\)
Trong đó:
- m: khối lượng chất giải phóng ở điện cực (gam)
- A: khối lượng mol nguyên tử của chất thu được ở điện cực
- n: số electron mà nguyên tử hoặc ion đã cho hoặc nhận
- I: cường độ dòng điện (A)
- t: thời gian điện phân (s)
- F: hằng số Faraday là điện tích của 1 mol electron hay điện lượng cần thiết để 1 mol electron chuyển dời trong mạch ở catot hoặc ở anot (F = 1,602.10-19.6,022.1023 ≈ 96500 C.mol-1)
3. Mở rộng định luật
Khối lượng vật chất giải phóng ở điện cực dương cũng bằng khối lượng vật chất bám vào cực âm.
Từ công thức định luật Fa-ra-đây, ta có thể suy ra các đại lượng cường độ dòng điện, thời gian điện phân, khối lượng mol nguyên tử (từ đó xác định tên nguyên tố).
 \(\begin{gathered}
\mathrm{m}=\frac{1}{\mathrm{~F}} \cdot \frac{\mathrm{A}}{\mathrm{n}} \mathrm{It} \Rightarrow \mathrm{I}=\frac{\mathrm{m} \cdot \mathrm{F} \cdot \mathrm{n}}{\text { A.t }} \\
\mathrm{m}=\frac{1}{\mathrm{~F}} \cdot \frac{\mathrm{A}}{\mathrm{n}} \mathrm{It}=>\mathrm{t}=\frac{\mathrm{m} \cdot \mathrm{F} \cdot \mathrm{n}}{\text { A.I }} \\
\mathrm{m}=\frac{1}{\mathrm{~F}} \cdot \frac{\mathrm{A}}{\mathrm{n}} \mathrm{It}=>\mathrm{A}=\frac{\mathrm{m} \cdot \mathrm{F} \cdot \mathrm{n}}{\mathrm{I} \cdot \mathrm{t}}=\frac{\mathrm{m} \cdot \mathrm{F} \cdot \mathrm{n}}{\mathrm{q}}
\end{gathered}\)
\(\begin{gathered}
\mathrm{m}=\frac{1}{\mathrm{~F}} \cdot \frac{\mathrm{A}}{\mathrm{n}} \mathrm{It} \Rightarrow \mathrm{I}=\frac{\mathrm{m} \cdot \mathrm{F} \cdot \mathrm{n}}{\text { A.t }} \\
\mathrm{m}=\frac{1}{\mathrm{~F}} \cdot \frac{\mathrm{A}}{\mathrm{n}} \mathrm{It}=>\mathrm{t}=\frac{\mathrm{m} \cdot \mathrm{F} \cdot \mathrm{n}}{\text { A.I }} \\
\mathrm{m}=\frac{1}{\mathrm{~F}} \cdot \frac{\mathrm{A}}{\mathrm{n}} \mathrm{It}=>\mathrm{A}=\frac{\mathrm{m} \cdot \mathrm{F} \cdot \mathrm{n}}{\mathrm{I} \cdot \mathrm{t}}=\frac{\mathrm{m} \cdot \mathrm{F} \cdot \mathrm{n}}{\mathrm{q}}
\end{gathered}\)
4. Bài tập định luật Faraday
Bài 1
Một bình điện phân đựng dung dịch AgNO3 có điện trở là 2,5 Ω. Canốt của bình điện phân bằng bạc (Ag) và hiệu điện thế đặt vào hai điện cực của bình là 10V. Tính khối lượng m của bạc bám vào catốt sau 16 phút 5 giây. Khối lượng nguyên tử của bạc là A=108 và hóa trị n = 1.
Bài giải:
Đổi 16 phút 5 giây = 965 giây
Cường độ dòng điện chạy qua bình điện phân là:
![]() \(\mathrm{I}=\frac{\mathrm{U}}{\mathrm{R}}=\frac{10}{2,5}=4\)
\(\mathrm{I}=\frac{\mathrm{U}}{\mathrm{R}}=\frac{10}{2,5}=4\)
Khối lượng bạc bám vào catốt sau 16 phút 5 giây là:
![]() \(\mathrm{m}=\frac{1}{\mathrm{~F}} \cdot \frac{\mathrm{A}}{\mathrm{n}} \mathrm{It}=\frac{1}{96500} \cdot \frac{108}{1} \cdot 4 \cdot 965=4,32(\mathrm{~g})\)
\(\mathrm{m}=\frac{1}{\mathrm{~F}} \cdot \frac{\mathrm{A}}{\mathrm{n}} \mathrm{It}=\frac{1}{96500} \cdot \frac{108}{1} \cdot 4 \cdot 965=4,32(\mathrm{~g})\)
Đáp án: 4,32 g
Bài 2: Người ta muốn bóc một lớp đồng dày d = 10μm trên một bản đồng diện tích S = 1cm2 bằng phương pháp điện phân. Cường độ dòng điện là 0,010 A. Tính thời gian cần thiết để bóc được lớp đồng. Cho biết đồng có khối lượng riêng là D = 8900 kg/m3, khối lượng mol 64 g/mol và hóa trị 2.
Bài giải:
Khối lượng đồng phải bóc đi:
m = D.V = D.S.d = 8900.1.10-4.10.10-6 = 8,9.10-6 (kg) = 8,9.10-3 (g)
Áp dụng công thức định luật Faraday:
![]() \(\mathrm{m}=\frac{\mathrm{AIt}}{\mathrm{F} \cdot \mathrm{n}}=>\mathrm{t}=\frac{\mathrm{m} \cdot 96500 \cdot \mathrm{n}}{\mathrm{AI}}=\frac{8,9 \cdot 10^{-3} \cdot 96500 \cdot 2}{64 \cdot 10^{-2}}=2683(\mathrm{~s})\)
\(\mathrm{m}=\frac{\mathrm{AIt}}{\mathrm{F} \cdot \mathrm{n}}=>\mathrm{t}=\frac{\mathrm{m} \cdot 96500 \cdot \mathrm{n}}{\mathrm{AI}}=\frac{8,9 \cdot 10^{-3} \cdot 96500 \cdot 2}{64 \cdot 10^{-2}}=2683(\mathrm{~s})\)
Đáp án: 2683 giây
Bài 3
Cho mạch điện như hình vẽ: Có bộ nguồn (E = 12 V; r = 0,4 Ω), R1 = 9Ω, R2 = 6Ω và một bình điện phân đựng dung dịch CuSO4, anôt bằng đồng Cu và điện trở của bình điện phân Rp = 4Ω. Tính:
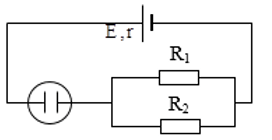
a) Cường độ dòng điện qua mạch chính.
b) Khối lượng đồng thoát ra ở cực dương trong 16 phút 5 giây.
Gợi ý đáp án
Khi điện phân một dung dịch muối mà kim loại anôt làm bằng chính kim loại ấy thì xảy ra hiện tượng cực dương ta (kim loại đề cập trong bài trên chính là Cu). Đến đây bài toán không có gì mới. Ta xem bình điện phân như một điện trở và tính toán bình thường. Riêng bình điện phân thì ta quan tâm tới dòng điện chạy qua bình điện phân, thời gian điện phân và khối lượng kim loại giải phóng ở điện cực. Lưu ý rằng khối lượng này tính bằng gam (g) chứ không phải bằng kilogam (kg)
a) Điện trở tương đương mạch ngoài:
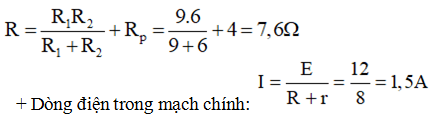
b) Khối lượng đồng thoát ra ở cực dương:
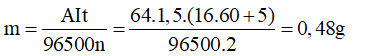
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:












 Đề thi học kì 1 Lớp 11
Đề thi học kì 1 Lớp 11
 Đề thi học kì 2 Lớp 11
Đề thi học kì 2 Lớp 11
 Soạn văn 11 Kết nối tri thức
Soạn văn 11 Kết nối tri thức
 Soạn văn 11 Chân trời sáng tạo
Soạn văn 11 Chân trời sáng tạo
 Soạn văn 11 Cánh Diều
Soạn văn 11 Cánh Diều
 Toán 11 Kết nối tri thức
Toán 11 Kết nối tri thức
 Toán 11 Chân trời sáng tạo
Toán 11 Chân trời sáng tạo
 Toán 11 Cánh Diều
Toán 11 Cánh Diều
 Hóa 11 KNTT
Hóa 11 KNTT









