Hướng dẫn giải 60 bài toán hàm số và đồ thị VD – VDC Tài liệu luyện thi THPT Quốc gia môn Toán
Hướng dẫn giải 60 bài toán hàm số và đồ thị VD – VDC là tài liệu gồm 35 trang tuyển chọn 60 bài toán hàm số và đồ thị mức độ vận dụng và vận dụng cao trích từ các đề thi thử THPT Quốc gia môn Toán năm học 2018 – 2019.
Các bài toán được phân tích và hướng dẫn giải chi tiết. Tài liệu nhằm hỗ trợ các em trong quá trình ôn tập chuẩn bị cho kỳ thi THPT Quốc gia 2019 môn Toán. Sau đây là nội dung chi tiết, mời các bạn cùng tham khảo và tải tài liệu tại đây.
Hướng dẫn giải 60 bài toán hàm số và đồ thị VD – VDC
1
HÀM SỐ VD_VDC
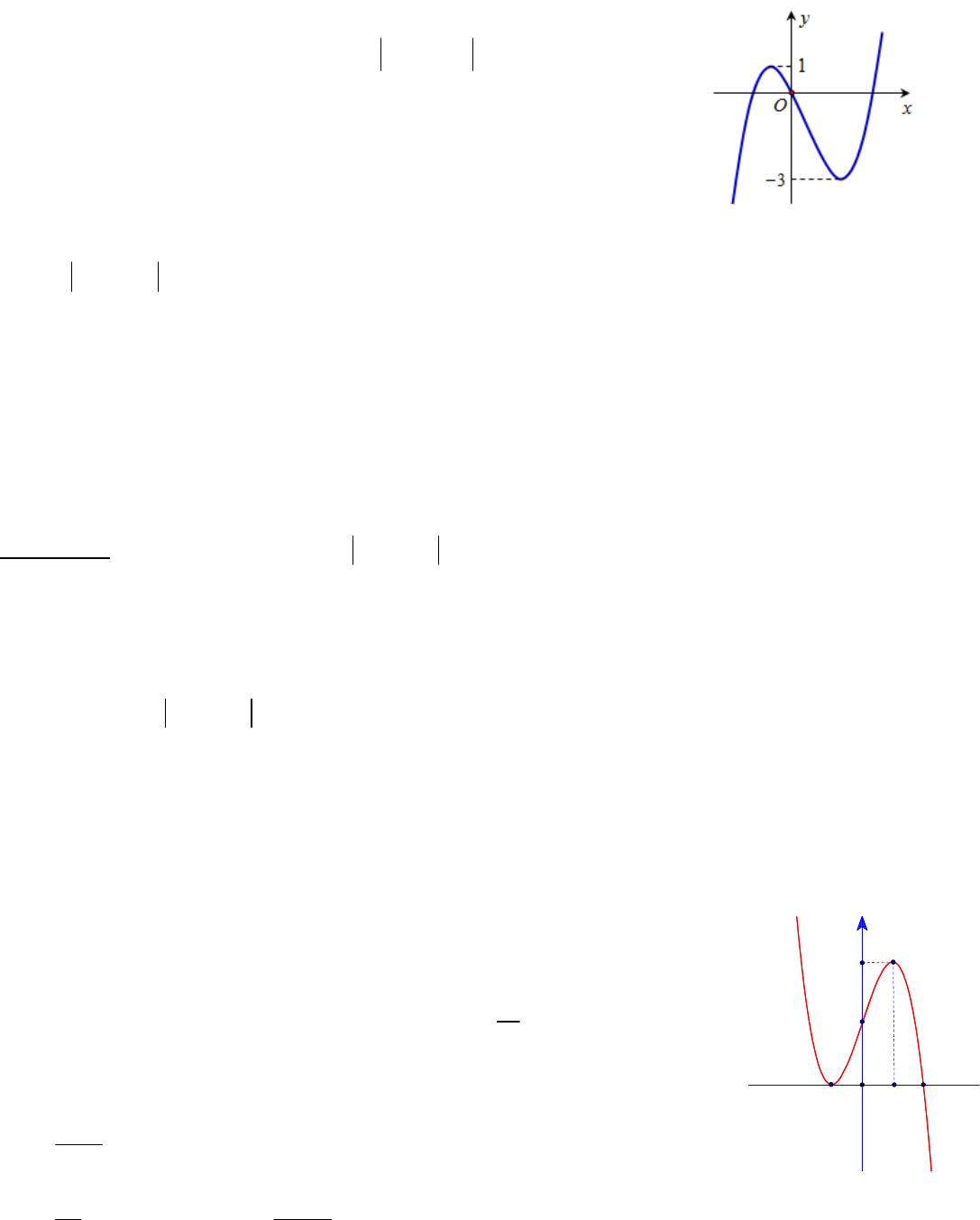
Câu 1: VD.Cho hàm số đa thức bậc ba
yfx
có đồ thị như hình bên. Tìm tất
cả các giá trị của tham số m để hàm số
yfxm
có ba điểm cực trị.
A. 1m hoặc 3m B. 3m hoặc 1m
C.
1m
hoặc
3m
D.
13m
: Đáp án là A
gồm và , trong đó có điểm cực trị
có 3 điểm cực trị có nghiệm đơn hoặc có nghiệm đơn và nghiệm kép
.
Trắc nghiệm: Số cực trị của hàm số bằng số cực trị của hàm số cộng số giao điểm của
(không tính tiếp điểm)
Hàm số có cực trị
Do đó hàm số có cực trị
phương trình có nghiệm đơn hoặc có nghiệm đơn và có nghiệm kép
.
Câu 2: VD.Cho hàm số
yfx
có đạo hàm
f
x
. Hàm số
yfx
liên tục
trên tập số thực và có đồ thị như hình vẽ. Biết
13
1,26
4
ff
. Tổng giá trị
lớn nhất và giá trị nhỏ nhất của hàm số
3
3gx f x f x
trên
1; 2
bằng:
A.
1573
64
B.
198
C.
37
4
D.
14245
64
1
2
0
0
f
xm khifxm L
Ly f x m
f
xmkhifxm L
L
1
L
2
L
yfxm
2
L
0fx m
111
3
1
m
m
3
1
m
m
yf
xm
yfx
f
xm
yfx
2
yf
xm
3
f
xm
111
3
1
m
m
3
1
m
m
y
2
2
-1
1
4
O
2
Đáp án là A
Bảng biến thiên
Ta có .
Xét trên đoạn .
Bảng biến thiên
.
Câu 3 (VD): Gọi
12
x,x
là hai điểm cực trị của hàm số
32
1
f(x) x 3x 2x
3
. Giá trị của
22
12
xx
bằng:
A.
13 B. 32 C. 4 D. 36
Cách giải:
Ta có:
22
f' x x 6x 2 f' x 0 x 6x 2 0 (*)
Có
12
x;x
là hai điểm cực trị của đồ thị hàm số
12
yf(x) x,x
là hai nghiệm của phương trình (*).
Áp dụng hệ thức Vi-et ta có:
12
12
xx 6
xx 2
22 2 2
12 12 12
xx(xx)2xx62.(2)40
Chọn C.
Câu 4 (VD): Biết rằng đồ thị hàm số
23322
31 1 3 4ya xb xcxd
có hai điểm cực trị là (1;-7), (2:-
8). Hãy xác định tổng
222 2
Mabcd
.
2
3. 3gx f xf x f x
1; 2
0gx
2
310fx f x
0fx
1
2
x
x
3
1;2
1573
min 1 1 3 1
64
gx g f f
3
A. -18 B. 18 C. 15 D. 8
Cách giải:
Ta có
22 3 2
'33 1 2 1 3yaxbxc
Từ giả thiết ta suy ra các điểm có tọa độ (1;-7), (2;-8) thuộc đồ thị hàm số đã cho và
1; 2xx
là hai điểm cực
trị của hàm số nên ta có hệ phương sau
23 2
232
22 3 2
22 3 2
31.8 1.464 8
31.1 1.134 7
3. 3 1 .1 2. 1 3 0
3. 3 1 .2 2.2. 1 3 0
ab cd
abcd
abc
abc
Đặt
23 2
31; 1;3; 4Aa Bb CcDd ta được hệ mới
2
3
2
842884282
312
773 1 9
19
32 0 32 0 12
312
12 4 0 12 4 0 12
412
ABCD ABCD A
a
ABCD A BC B
b
ABC ABC C
c
ABC ABC D
d
2
2
222 2
2
2
1
4
18
4
9
a
b
Mabcd
c
d
Chọn B.
Câu 5 (VD): Tìm m để đường thẳng
y2xm
cắt đồ thị hàm số
x3
y
x1
tại hai điểm M, N sao cho độ dài
MN nhỏ nhất:
A.
3
B. -1 C. 2 D. 1
Cách giải:
Phương trình hoành độ giao điểm của 2 đồ thị hàm số là:
2
x3
2x m x 1 2x (m 1)x m 3 0
x1
(*)
Ta có:
2
22
m 1 8(m 3) m 6m 25 (m 3) 16 0 m
(*) luôn có hai nghiệm phân biệt
12
x,x
với mọi m.
Áp dụng hệ thức Vi-et ta có:
12
12
m1
xx
2
m3
xx
2
Gọi
11 2 2
M(x ;2x m), N(x ;2x m)
là hai giao điểm của 2 đồ thị hàm số.
Khi đó ta có:
Chia sẻ bởi: 
Trịnh Thị Thanh
Trịnh Thị Thanh Liên kết tải về
Link Download chính thức:
Hướng dẫn giải 60 bài toán hàm số và đồ thị VD – VDC 577,4 KB 20/04/2019 Download
Có thể bạn quan tâm
-
Tập làm văn lớp 5: Tả người bà yêu quý của em
-
Cách thay thế từ/cụm từ trong bài nghị luận văn học
-
Tập làm văn lớp 5: Tả cảnh buổi sáng trên cánh đồng
-
Tổng hợp dàn ý bài Câu cá mùa thu (9 Mẫu)
-
Soạn bài Tục ngữ về thiên nhiên, lao động và con người, xã hội (2) - Cánh diều 7
-
Cảm nhận về bài thơ Câu cá mùa thu của Nguyễn Khuyến
-
Mẫu vở tập tô chữ cho bé - Tập tô chữ cái cho bé chuẩn bị vào lớp 1
-
Phân tích bài thơ Câu cá mùa thu của Nguyễn Khuyến (3 Dàn ý + 19 mẫu)
-
Văn mẫu lớp 9: Nghị luận về vai trò của lao động đối với con người
-
Văn mẫu lớp 10: Dàn ý phân tích bài thơ Nắng mới (5 mẫu)
Sắp xếp theo
