Hai đường thẳng song song: Lý thuyết và bài tập Chứng minh 2 đường thẳng song song

Hai đường thẳng song song là gì? Chứng minh 2 đường thẳng song song như thế nào? Tính chất hai đường thẳng song song ra sao? Là câu hỏi được rất nhiều bạn học sinh quan tâm.

2 đường thẳng song song là một chủ đề rất quan trọng trong chương trình toán học phổ thông các bạn sẽ được học từ lớp 6 đến lớp 11 và được ứng dụng rất nhiều trong thực tiễn. Trong bài viết hôm nay Eballsviet.com sẽ giới thiệu đến các bạn toàn bộ kiến thức về Hai đường thẳng song song như dấu hiệu, tính chất, cách chứng minh và một số bài tập vận dụng. Thông qua tài liệu này các bạn có thêm nhiều gợi ý tham khảo, trau dồi kiến thức để nhanh chóng giải được các bài tập Toán.

1. Hai đường thẳng song song

Hai đường thẳng song song (trong mặt phẳng) là hai đường thẳng không có điểm chung

2. Dấu hiệu nhận biết 2 đường thẳng song song

Dấu hiệu 1: Dựa vào khái niệm hai đường thẳng song song.

Dấu hiệu 2: Dựa vào một đường thẳng cắt hai đường thẳng cần xét.

Nếu một đường thẳng c cắt hai đường thẳng a, b và trong các góc tạo thành có một cặp góc so le trong bằng nhau (hoặc một cặp góc đồng vị bằng nhau) thì a và b song song với nhau.

Dấu hiệu 3: Dựa vào quan hệ từ vuông góc đến song song

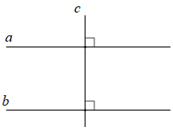
Cho đường thẳng a vuông góc với c, đường thẳng b vuông góc với c (a, b phân biệt) thì đường thẳng a song song với đường thẳng b (Hình vẽ trên)

Ta có công thức:

\(\left\{\begin{array}{l} \mathrm{a} \perp \mathrm{c} \\ \mathrm{b} \perp \mathrm{c} \end{array} \Rightarrow \mathrm{a} / / \mathrm{b}\right.\)

Dấu hiệu 4: Dựa vào tính cùng song song

Hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì chúng song song với nhau

3. Tính chất hai đường thẳng song song

Nếu một đường thẳng cắt hai đường thẳng song song thì

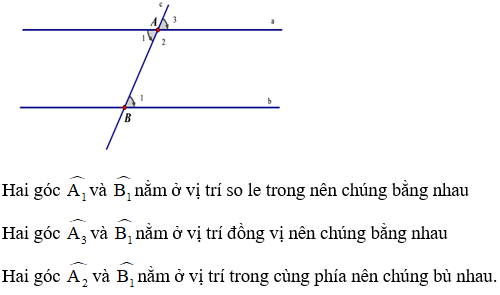
- Hai góc so le trong bằng nhau

- Hai góc đồng vị bằng nhau

- Hai góc trong cùng phía bù nhau

Cho đường thẳng c cắt hai đường thẳng song song a và b như hình vẽ:

4. Cách vẽ hai đường thẳng song song

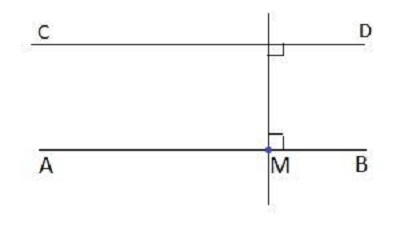
Vẽ đường thẳng CD đi qua điểm E và song song với đường thẳng AB cho trước.

Ta có thể vẽ như sau:

Vẽ đường thẳng MN đi qua điểm E và vuông góc với đường thẳng AB.

Vẽ đường thẳng CD đi qua điểm E và vuông góc với đường thẳng MN ta được đường thẳng CD song song với đường thẳng AB

5. Chứng minh 2 đường thẳng song song

- Phương pháp 1: Tìm hai góc trong cùng phía bù nhau.

- Phương pháp 2: Tìm hai góc so le trong bằng nhau.

- Phương pháp 3: Tìm các góc đồng vị bằng nhau.

- Phương pháp 4: Áp dụng tiên đề Ơ-clít về đường thẳng song song: "Qua một điểm nằm ngoài đường thẳng chỉ có một đường thẳng song song với đường thẳng đó".

- Phương pháp 5: Tìm ra hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba.

- Phương pháp 6: Tìm ra hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba.

6. Bài tập Hai đường thẳng song song

Bài tập 1: Cho tam giác ABC, M là trung điểm của BC. Trên tia đối của MA, lấy điểm D sao cho MA = MD. Chứng minh: AB // CD.

Bài tập 2: Cho tam giác ABC, M và N lần lượt là trung điểm của AB, AC. Trên tia đối của tia MC, lấy điểm D sao cho MD = MC. Trên tia đối của tia NB, lấy điểm E sao cho NE = NB. Chứng minh: DE // BC.

Bài tập 3: Cho tam giác cân ABC có AB = AC. Trên các cạnh AB và AC, lấy lần lượt điểm D và E sao cho AD = AE. Chứng minh: DE // BC.