Đề thi tuyển sinh lớp 10 THPT chuyên tỉnh Khánh Hòa năm học 2013 - 2014 môn Toán
Eballsviet.com Học tập Thi vào 10

Đề thi tuyển sinh lớp 10 THPT chuyên tỉnh Khánh Hòa năm học 2013 - 2014 môn Toán Sở GD-ĐT Khánh Hòa

Tải về Bình luận
  • 1

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KHÁNH HÒA

ĐỀ CHÍNH THỨC

ĐỀ THI TUYỂN SINH VÀO LỚP 10 THPT CHUYÊN
NĂM HỌC 2013 - 2014

MÔN THI: TOÁN (KHÔNG CHUYÊN)
Thời gian làm bài: 120 phút (không kể thời gian giao đề)
Ngày thi: 21/06/2013


Bài 1: (2,0 điểm) (không dùng máy tính cầm tay)

1. Chứng minh:

2. Cho biểu thức: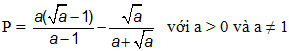

Rút gọn rồi tính giá trị của P tại a = 20142

Bài 2: (2,0 điểm)

1. Tìm x biết:

2. Giải hệ phương trình: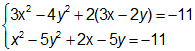

Bài 3: (2,0 điểm)

Trong mặt phẳng tọa độ Oxy, cho parapol

1. Vẽ đồ thị (P)

2. Gọi M là điểm thuộc (P) có hoành độ x = 2. Lập phương trình đường thẳng đi qua điểm M đồng thời cắt trục hoành và trục tung lần lượt tại hai điểm phân biệt A và B sao cho diện tích tam giác OMA gấp đôi diện tích tam giác OMB.

Bài 4: (4,0 điểm)

Cho đường tròn (O; 3cm) có hai đường kính AB và CD vuông góc với nhau. Gọi M là điểm tùy ý thuộc đoạn OC (M khác O và C). Tia BM cắt đường tròn (O) tại N

1. Chứng minh AOMN là một tứ giác nội tiếp

2. Chứng minh ND là phân giác của góc ANB

3. Tính

4. Gọi E và F lần lượt là hai điểm thuộc các đường thẳng AC và AD sao cho M là trung điểm của EF. Nếu cách xác định các điểm E, F và chứng minh rằng tổng (AE + AF) không phụ thuộc vào vị trí của điểm M.

Download tài liệu để xem thêm chi tiết

Chia sẻ bởi: 👨 Nguyễn Thu Ngân
Liên kết tải về
Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!
Số điện thoại này đã được xác thực!
Bạn có thể dùng Sđt này đăng nhập tại đây!
Lỗi gửi SMS, liên hệ Admin
Sắp xếp theo
👨

Tài liệu tham khảo khác

Chủ đề liên quan

Có thể bạn quan tâm

Xem thêm

Mới nhất trong tuần

Đóng
Chỉ thành viên Download Pro tải được nội dung này! Download Pro - Tải nhanh, website không quảng cáo! Tìm hiểu thêm
Mua Download Pro 79.000đ