Đề thi Tìm kiếm tài năng Toán học trẻ lớp 9 năm 2019 Đáp án đề thi MYTS lớp 9
Đề thi tìm kiếm tài năng Toán học trẻ lớp 9 bao gồm 20 câu hỏi, thời gian 120 phút. Với rất nhiều câu hỏi mang tính thực tế, hình ảnh sinh động, cuộc thi này nhằm phát hiện những học sinh có năng khiếu Toán học.
Sau đây Eballsviet.com xin gửi đến các vị phụ huynh và các em học sinh yêu Toán toàn bộ đề thi và đáp án (Vòng 1) Kỳ thi Tìm kiếm tài năng Toán học trẻ lớp 9 năm 2019. Mời các em cùng tham khảo nội dung chi tiết dưới đây:
Đề thi Tìm kiếm tài năng Toán học trẻ lớp 9 có đáp án
9
HỘI TOÁN HỌC VIỆT NAM
MYTS 2019
MYTS 2019
Tìm kiếm Tài năng Toán học trẻ
Ngày thi: 24/03/2019
Thời gian làm bài: 120 phút
999
Câu 1. Giải phương trình
1 + 𝑥 + 2)
1 + 𝑥 + 3)𝑥 + 5) 2019𝑥 + 1.
Câu 2. Tìm số tự nhiên 𝑛 sao cho 𝑛 và 𝑛 + 19 đều là các số chính phương.
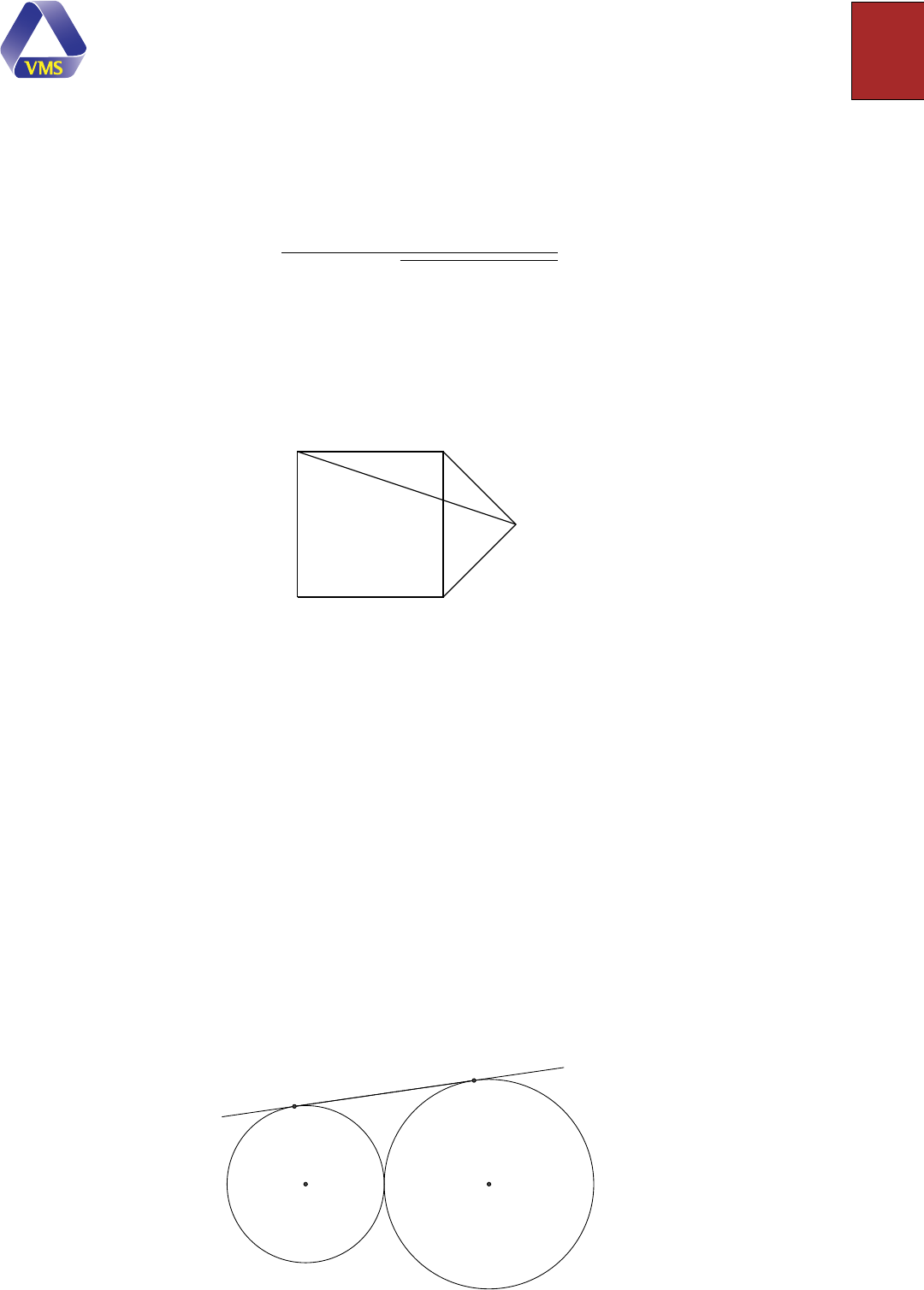
Câu 3. Trong hình dưới đây, 𝐴𝐵𝐶𝐷 là hình vuông có cạnh bằng 2, tam giác 𝐵𝐸𝐶
vuông cân tại 𝐸. Tính độ dài đoạn thẳng 𝐴𝐸.
D
A B
C
E
Câu 4. Xét các số thực 𝑥, 𝑦, 𝑧 thoả mãn 𝑥
2
+ 2𝑦
2
+ 9𝑧
2
12. Tìm giá trị lớn nhất của
biểu thức 𝑇 𝑥𝑦 + 3𝑦𝑧.
Câu 5. Cho 𝐴 là tổng tất cả các ước dương của 2
2019
. Tìm số dư trong phép chia 𝐴
cho 3.
Câu 6. Tìm tất cả các giá trị của tham số 𝑎 sao cho phương trình 𝑥
2
− 9𝑥 + 𝑎 0 có
hai nghiệm thực 𝑥
1
, 𝑥
2
thoả mãn 𝑥
1
− 2)
2
+ 𝑥
2
− 3)
2
10.
Câu 7. Một cái chảo có thể đựng được tối đa bốn miếng đậu. Dùng chảo đó, để rán
chín một mặt của một miếng đậu cần 1 phút. Hỏi cần ít nhất bao nhiêu phút để rán
chín cả hai mặt mười miếng đậu?
Câu 8. Cho hai đường tròn 𝑂
1
) và 𝑂
2
) tiếp xúc với nhau, và 𝐴𝐵 là một tiếp tuyến
chung ngoài của chúng. Biết 𝐴𝐵 18, bán kính đường tròn 𝑂
1
) bằng 3. Tính bán kính
của đường tròn 𝑂
2
).
O
1
O
2
A
B
1
999
Câu 9. Cho ba số 𝑎, 𝑏, 𝑐 khác 0, đôi một phân biệt và thoả mãn 𝑎 +
4
𝑏
𝑏 +
4
𝑐
𝑐 +
4
𝑎
.
Tính |𝑎𝑏𝑐|.
Câu 10. Cho 𝑀 11 ×21 ×31 ×··· ×91 ×101. Tìm số dư trong phép chia 𝑀 cho 100.
Câu 11. Với mỗi số nguyên dương 𝑘, đặt 𝑓𝑘)
1
𝑘 + 2) × 𝑘)
. Tìm số nguyên dương 𝑛
lớn nhất sao cho
𝑓1) + 𝑓 2) + ··· + 𝑓 𝑛) <
1
2
−
1
2019
.
(𝑘 là tích của 𝑘 số nguyên dương đầu tiên.)
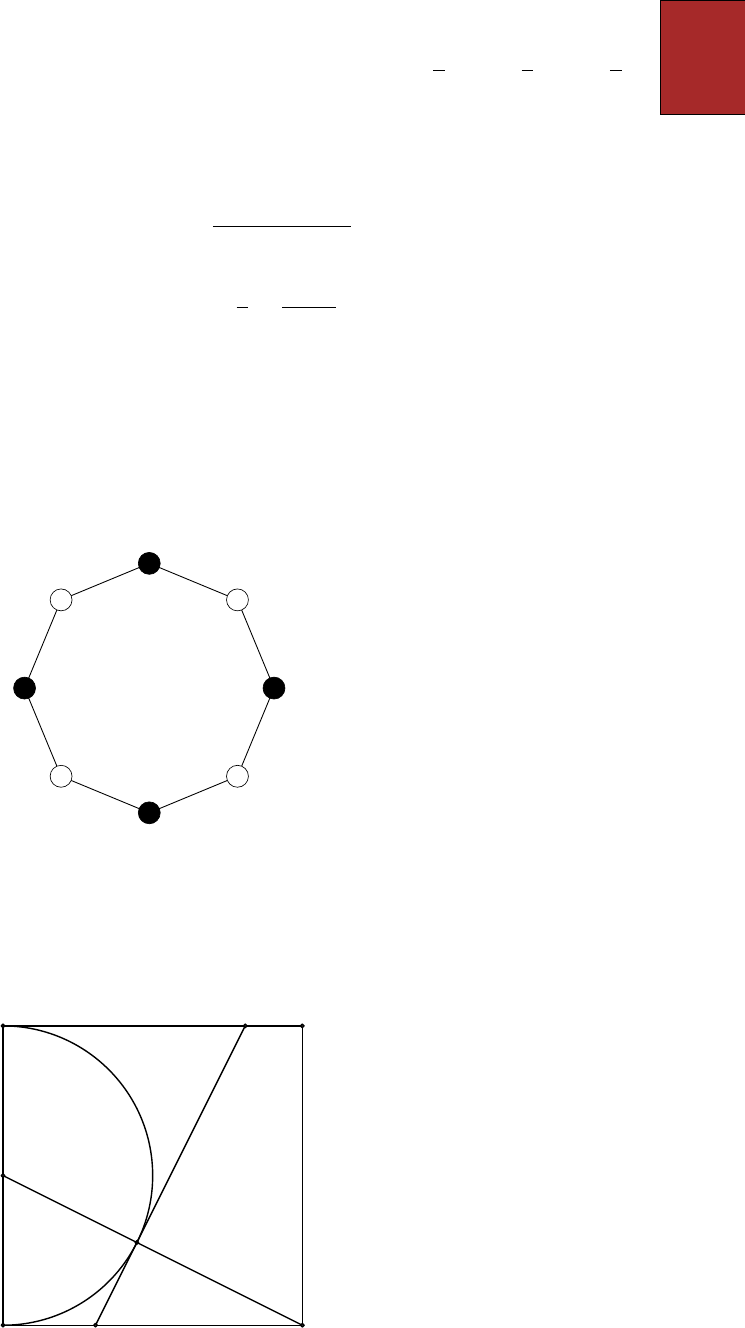
Câu 12. Người ta ghi vào mỗi đỉnh của bát giác ở hình dưới đây một số thực khác 0,
sao cho số tại mỗi đỉnh màu đen bằng tổng hai số tại hai đỉnh màu trắng kề với nó, số
tại mỗi đỉnh màu trắng bằng tích hai số tại hai đỉnh màu đen kề với nó. Tính tổng tất
cả các số đã ghi.
Câu 13. Trong hình dưới đây, 𝐴𝐵𝐶𝐷 là hình vuông có cạnh bằng 2, 𝑂 là trung điểm
𝐴𝐷, 𝐸𝐹 tiếp xúc với nửa đường tròn đường kính 𝐴𝐷 tại 𝑀. Tính độ dài đoạn thẳng
𝐸𝐹 .
A B
C
D
O
M
E
F
Câu 14. Cho 𝑥, 𝑦 là hai số thực thoả mãn 𝑥 + 𝑦 12 và [𝑥 + 2[𝑦 13. Tìm tất cả các
giá trị của [𝑥.
([𝑥 kí hiệu phần nguyên của số thực 𝑥.)
2
999
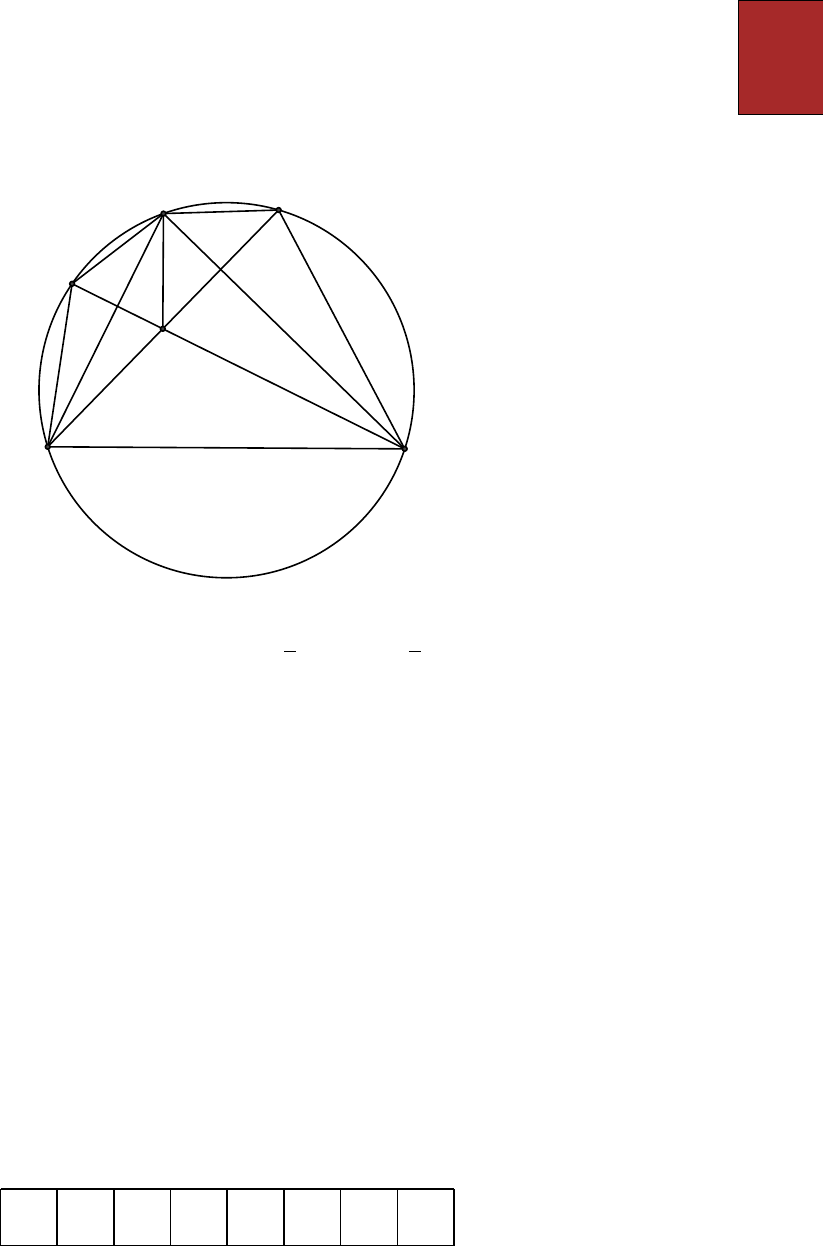
Câu 15. Trong hình vẽ dưới đây, 𝐻 là trực tâm của tam giác 𝐴𝐵𝐶. Biết diện tích tam
giác 𝐴𝐵𝐸 bằng 4, diện tích tam giác 𝐴𝐶𝐷 bằng 6 và độ dài đoạn 𝐴𝐻 bằng 4. Tính độ
dài đoạn thẳng 𝐵𝐶.
B
C
A
H
D
E
Câu 16. Tìm tất cả các số thực 𝑎 sao cho 𝑎 +
√
5 và 𝑎
2
+
√
5 đều là số hữu tỉ.
Câu 17. Hỏi từ tất cả các ước nguyên dương của 20
2019
có thể chọn được tối đa bao
nhiêu số sao cho trong các số được chọn không có số nào là bội của số khác?
Câu 18. Trong hộp có 100 viên bi, gồm bi vàng, bi xanh, bi trắng và bi đỏ. Biết rằng
nếu lấy 90 viên bi bất kì trong hộp, thì chắc chắn có bốn viên đôi một khác màu. Hỏi
phải lấy ít nhất bao nhiêu viên bi để chắc chắn có ba viên đôi một khác màu?
Câu 19. Hỏi từ 30 số nguyên dương đầu tiên, có thể chọn được tối đa bao nhiêu số,
sao cho mỗi số được chọn không là ước của tích tất cả các số được chọn còn lại?
Câu 20. Cho dãy gồm 8 ô vuông, được đánh số như ở hình dưới đây. Khi nhảy từ ô số
𝑚 sang ô số 𝑛, ta nói rằng đã thực hiện một bước nhảy có độ dài bằng |𝑚 − 𝑛|.
Xuất phát từ ô số 0, một con ếch nhảy liên tiếp vào các ô còn lại sao cho độ dài của
mỗi bước nhảy bằng 1, 2, hoặc 4, và không nhảy vào ô nào quá 1 lần. Hỏi tổng độ dài
các bước nhảy có thể nhận giá trị lớn nhất bằng bao nhiêu?
0 1 2 3 4 5 6 7
3
Chia sẻ bởi: 
Trịnh Thị Thanh
Trịnh Thị Thanh Liên kết tải về
Link Download chính thức:
Đề thi Tìm kiếm tài năng Toán học trẻ lớp 9 năm 2019 Download
Có thể bạn quan tâm
-
Bài dự thi những tấm gương tâm huyết sáng tạo học theo lời Bác năm 2023
-
Tập làm văn lớp 5: Tả cảnh bình minh trên quê hương em
-
Văn mẫu lớp 7: Cảm nghĩ về ngày Tết cổ truyền quê em
-
Văn mẫu lớp 9: Đóng vai ngư dân kể lại bài thơ Đoàn thuyền đánh cá
-
Bài thơ Lượm - Sáng tác năm 1949, Tố Hữu
-
Mẫu 09/ĐK: Đơn đăng ký biến động đất đai
-
Tranh tô màu Pikachu - Bộ tranh tô màu Pikachu đẹp
-
Giáo án Toán lớp 1 (Sách mới) - Giáo án Toán lớp 1 (trọn bộ 5 sách)
-
Tuyển tập đề thi học sinh giỏi môn Toán lớp 3
-
Thuyết minh về Thành Cổ Loa (2 Dàn ý + 5 mẫu)
Sắp xếp theo
