Đề thi học sinh giỏi lớp 12 THPT tỉnh Thanh Hóa năm học 2010 - 2011 môn Toán (Có đáp án) Sở GD&ĐT Thanh Hóa
SỞ GIÁO DỤC VÀ ĐÀO TẠO
|
KỲTHI CHỌN HỌC SINH GIỎI LỚP 12 THPT
|
MÔN THI: TOÁN
Thời gian làm bài: 180 phút (không kể thời gian giao đề)
--------------------------------------------------------------------------------
Câu I. (4,0 điểm).
Cho hàm số y = x3 - (m + 1)x2 - (4 - m2)x - 1 - 2m (m là tham số thực), có đồ thị là (Cm)
1) Khảo sát sự biến thiên và vẽ đồ thị hàm số với m = − 1
2) Tìm các giá trị của m để đồ thị (Cm) có hai tiếp tuyến vuông góc với nhau.
Câu II. (6,0 điểm).
1) Giải phương trình: cos2x + cos3x - sinx - cos4x = sin6x.
2) Giải bất phương trình: ![]() (x thuộc R)
(x thuộc R)
3) Tìm số thực a để phương trình: 9x + 9 = a3xcos(πx), chỉ có duy nhất một nghiệm thực.
Câu III. (2,0 điểm).
Tính tích phân: 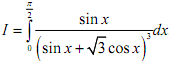
Câu IV. (6,0 điểm).
1) Cho tứ diện đều ABCD có độ dài cạnh bằng 1. Gọi M, N lần lượt là hai điểm thuộc các cạnh AB, AC sao cho mặt phẳng (DMN) vuông góc với mặt phẳng (ABC). Đặt AM = x, AN = y. Tìm x, y để diện tích toàn phần của tứ diện DAMN nhỏ nhất.
2) Trên mặt phẳng toạ độ Oxy cho đường thẳng Δ: x − y + 5 = 0 và hai elíp:![]() có cùng tiêu điểm. Biết rằng (E2) đi qua điểm M thuộc đường thẳng Δ. Tìm toạ độ điểm M sao cho elíp (E2) có độ dài trục lớn nhỏ nhất.
có cùng tiêu điểm. Biết rằng (E2) đi qua điểm M thuộc đường thẳng Δ. Tìm toạ độ điểm M sao cho elíp (E2) có độ dài trục lớn nhỏ nhất.
3) Trong không gian , Oxyz cho điểm M(0;2;0) và hai đường thẳng
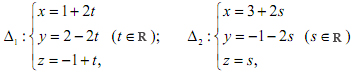
Viết phương trình mặt phẳng (P) đi qua M song song với trục Ox, sao cho (P) cắt hai đường thẳng Δ1, Δ2 lần lượt tại A, B thoả mãn AB = 1
Câu V. (2,0 điểm).
Cho các số thực a, b, c thoả mãn: 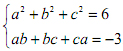
Tìm giá trịlớn nhất của biểu thức: P = a6 + b6 + c6
Download tài liệu để xem thêm chi tiết
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:












 Đề thi học kì 1 Lớp 12
Đề thi học kì 1 Lớp 12
 Đề thi giữa học kì 1 Lớp 12
Đề thi giữa học kì 1 Lớp 12
 Đề thi giữa học kì 2 Lớp 12
Đề thi giữa học kì 2 Lớp 12
 Đề thi học kì 2 Lớp 12
Đề thi học kì 2 Lớp 12
 Soạn Văn 12 KNTT
Soạn Văn 12 KNTT
 Soạn Văn 12 CTST
Soạn Văn 12 CTST
 Soạn Văn 12 Cánh Diều
Soạn Văn 12 Cánh Diều
 Văn 12
Văn 12
 Toán 12 Chân trời sáng tạo
Toán 12 Chân trời sáng tạo









