Đề thi học sinh giỏi giải toán trên Máy tính cầm tay tỉnh Thừa Thiên Huế - Khối 9 (2009 - 2010) Sở GD&ĐT Thừa Thiên Huế

Bài 1: (5 điểm)

Tính giá trị của biểu thức: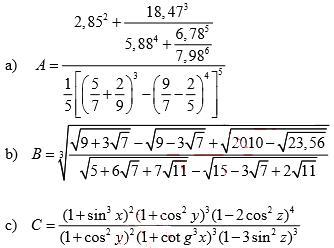

biết cosx = 0,9534; siny = 0,7685; tgz = 0,7111

Bài 2: (5 điểm)

Cho đa thức P(x) = x⁵ + ax⁴ + bx³ + cx² + dx + e có giá trị là: -14; - 9; 0;13; 30 khi x lần lượt nhận giác trị là 1; 2; 3; 4; 5.

a) Tìm biểu thức hàm của đa thức P(x) .

b) Tính giá trị chính xác của P(17), P(25), P(59), P(157).

Bài 3: (5 điểm)

a) Số chính phương P có dạng . Tìm các chữ số a, b, c biết rằng a³ + b³ + c³ = 349

b) Số chính phương Q có dạng . Tìm các chữ số c, d biết rằng tổng các chữ số của Q chia hết cho 5. Nêu sơ lược qui trình bấm phím.

Bài 4: (5 điểm)

Ba vòi nước cùng chảy vào một bể ban đầu chưa có nước sau 315/193 giờ thì đầy bể. Biết rằng, nếu chảy một mình vào bể chưa có nước thì vòi thứ hai chảy đầy bể chậm hơn vòi thứ nhất 30 phút; vòi thứ ba chảy chậm hơn vòi thứ hai 15 phút. Tính thời gian chảy một mình để đầy bể của mỗi vòi nước.

Bài 5: (5 điểm)

Cho các đa thức: P(x) = 120x⁵ - 98x⁴ - 335x³ - 93x² - 86x + 72 và Q(x) = 12x² - 11x - 36

a) Phân tích các đa thức P(x) và Q(x) thành nhân tử.

b) Tìm các nghiệm đúng hoặc gần đúng của phương trình P(x) = Q(x)(x² + 3)

Bài 6: (5 điểm)

Tìm các chữ số hàng đơn vị, hàng chục và hàng trăm của số tự nhiên:

Bài 7: (5 điểm)

Cho dãy hai số u_n xác định bởi:

a. Tính các giá trị chính xác của u₃, u₄, u₁₅, u₁₆, u₁₇, u₁₈, u₁₉, u₂₀. Viết qui trình bấm phím.

b. Lập công thức truy hồi tính u_n+2 theo một biểu thức bậc nhất đối với u_n+1 và u_n. Chứng minh.

Bài 8: (5 điểm)

Cho hình chóp ngũ giác đều S.ABCDE, cạnh đáy a = AB = 8dm, cạnh bên l = SA = 12dm

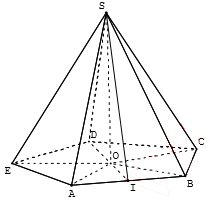
a) Tính gần đúng diện tích đa giác đáy ABCDE.

b) Tính gần đúng diện tích xung quanh và thể tích của hình chóp S.ABCDE.

Bài 9: (5 điểm)

Bác An gửi tiết kiệm số tiền ban đầu là 20 triệu đồng theo kỳ hạn 3 tháng với lãi suất 0,72%/tháng. Sau một năm, bác An rút cả vốn lẫn lãi và gửi lại theo kỳ hạn 6 tháng với lãi suất 0,78%/tháng. Gửi đúng một số kỳ hạn 6 tháng và thêm một số tháng nữa thì bác An phải rút tiền trước kỳ hạn để sửa chữa nhà được số tiền là 29451583,0849007 đồng (chưa làm tròn). Hỏi bác An gửi bao nhiêu kỳ hạn 6 tháng, bao nhiêu tháng chưa tới kỳ hạn và lãi suất không kỳ hạn mỗi tháng là bao nhiêu tại thời điểm rút tiền?

Biết rằng gửi tiết kiệm có kỳ hạn thì cuối kỳ hạn mới tính lãi và gộp vào vốn để tính kỳ hạn sau, còn nếu rút tiền trước kỳ hạn, thì lãi suất tính từng tháng và gộp vào vốn để tính tháng sau. Nêu sơ lược quy trình bấm phím trên máy tính để giải.

Bài 10: (6 điểm)

Trong mặt phẳng tọa độ Oxy, cho các điểm: A(-4; 2), B(-1; 3), C(6; 1), D(-3; -2)

a) Tứ giác ABCD là hình gì? Tính chu vi, diện tích và chiều cao của tứ giác ABCD.

b) Tính gần đúng hệ số góc của đường thẳng chứa tia phân giác trong góc A của tam giác CAD và tọa độ giao điểm E của tia phân giác trong góc A với cạnh CD.

c) Tính gần đúng diện tích tam giác ADE.

Download tài liệu để xem thêm chi tiết