Đề thi học sinh giỏi giải toán trên máy tính cầm tay tỉnh Thanh Hóa năm 2012 môn Toán lớp 9 - Có đáp án Sở GD&ĐT Thanh Hóa

Tải về Bình luận

SỞ GIÁO DỤC VÀ ĐÀO TẠO
THANH HÓA
(Đề thi chính thức)

KỲTHI CHỌN HỌC SINH GIỎI LỚP 9 THCS
GIẢI TOÁN TRÊN MÁY TÍNH CẦM TAY NĂM HỌC 2011- 2012

MÔN THI: TOÁN
Thời gian làm bài: 150 phút (không kể thời gian giao đề)
--------------------------------------------------------------------------------

Câu 1: (2 điểm)

Hãy tính giá trị của biểu thức:

Câu 2: (2 điểm)

Tìm nghiệm nguyên của phương trình: x + xy + y = 7

Câu 3: (2 điểm)

Cho tam giác ABC có AB = 3cm; BC = 4cm ; CA = 5cm. Các đường cao BH, đường phân giác BD, đường trung tuyến BP chia tam giác thành 4 phần. Hãy tính diện tích mỗi phần

Câu 4: (2 điểm)

Giải phương trình: (x² + 3x + 2) (x² + 7x + 12) = 3

Câu 5: (2 điểm)

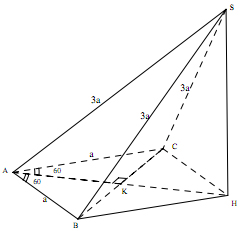
Cho hình chóp S.ABC có AB = AC = a , góc BAC bằng 120⁰, SA = SB = SC = 3a.

a. Tính thể tích hình chóp S.ABC.

b. Áp dụng với

Câu 6: (2 điểm)

Tính tổng:

Câu 7: (2 điểm)

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. SA = a và SA vuông góc với mặt phẳng ABCD. Kẻ AE⊥SB, AF⊥SD. Gọi K là giao điểm của SC với mặt phẳng AEF.

a. Tính diện tích tứ giác AEKF.

b. Áp dụng với

Câu 8: (2 điểm)

Tìm nghiệm nguyên của hệ phương trình: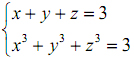

Câu 9: (2 điểm)

Cho tam giác ABC có BC = a, CA = b, BA = c. Từ một điểm M trong tam giác hạcác đường vuông góc MA₁, MB₁và MC₁xuống các đường thẳng BC, CA và AB. Với vị trí nào của M thì 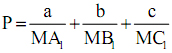đạt giá trị nhỏ nhất. Xác định giá trị nhỏ nhất đó với

Câu 10: (2 điểm)

Cho các số thực dương x, y, z thoả mãn: x ≥ y ≥ z và 32 - 3x² = z² = 16 - 4y². Tìm giá trị lớn nhất của A = xy + yz + zx. Với x, y, z bằng bao nhiêu thì A đạt giá trị lớn nhất.

Download tài liệu để xem thêm chi tiết

Chia sẻ bởi:

Tải về

Liên kết tải về

Đề thi học sinh giỏi giải toán trên máy tính cầm tay tỉnh Thanh Hóa năm 2012 môn Toán lớp 9 - Có đáp án 271 KB Tải về

Tìm thêm: Toán 9

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!