Chuyên đề góc và khoảng cách trong không gian Tài liệu ôn thi THPT Quốc gia 2019
Chuyên đề góc và khoảng cách trong không gian là tài liệu cực kì hữu ích mà Eballsviet.com muốn giới thiệu đến các bạn học sinh lớp 12 cùng tham khảo.
Tài liệu bao gồm 66 trang được biên soạn bởi thầy Nguyễn Hữu Nhanh Tiến hướng dẫn phương pháp giải các dạng toán chuyên đề góc và khoảng cách trong không gian. Nội dung chi tiết, mời các bạn cùng tham khảo và tải tài liệu tại đây.
Chuyên đề góc và khoảng cách trong không gian
Ð L
A
T
E
X Hóa Nguyễn Hữu Nhanh Tiến h /ToanTienNhanh
Hướng tới kì thi THPTQG 2019
GÓC - KHOẢNG CÁCH
§1. Các dạng toán liên quan đến tính Góc
1. 1 Góc giữa hai đường thẳng
Góc giữa hai đường thẳng a và b trong không gian là góc giữa hai đường thẳng a
0
và b
0
cùng đi qua
một điểm và lần lượt song song với a và b.
a
a
0
b
b
0
O
L Để xác định góc giữa hai đường thẳng a và b ta có thể lấy điểm O thuộc một trong hai đường
thẳng đó rồi vẽ một đường thẳng qua O và song song với đường thẳng còn lại.
L Nếu
#»
u và
#»
v lần lượt là vec-tơ chỉ phương của a và b, đồng thời (
#»
u ,
#»
v ) = α thì góc giữa hai
đường thẳng a và b bằng α nếu 0
◦
≤ α ≤ 90
◦
và bằng 180
◦
− α nếu 90
◦
< α ≤ 180
◦
.
L Nếu a và b là hai đường thẳng song song hoặc trùng nhau thì góc giữa chúng bằng 0
◦
.
!
Xác định góc giữa hai đường thẳng trong không gian. Ta thường có hai phương pháp để giải
quyết cho dạng toán này.
¹ Phương pháp 1: Sử dụng định nghĩa góc giữa hai đường thẳng, kết hợp sử dụng hệ thức
lượng trong tam giác (định lý cos, công thức trung tuyến).
¹ Phương pháp 2: Sử dụng tích vô hương của hai vec-tơ.
Ví dụ 1.
161 -Bùi Thị Xuân Tp Huế 1 TT Quốc Học Huế
Ð L
A
T
E
X Hóa Nguyễn Hữu Nhanh Tiến h /ToanTienNhanh
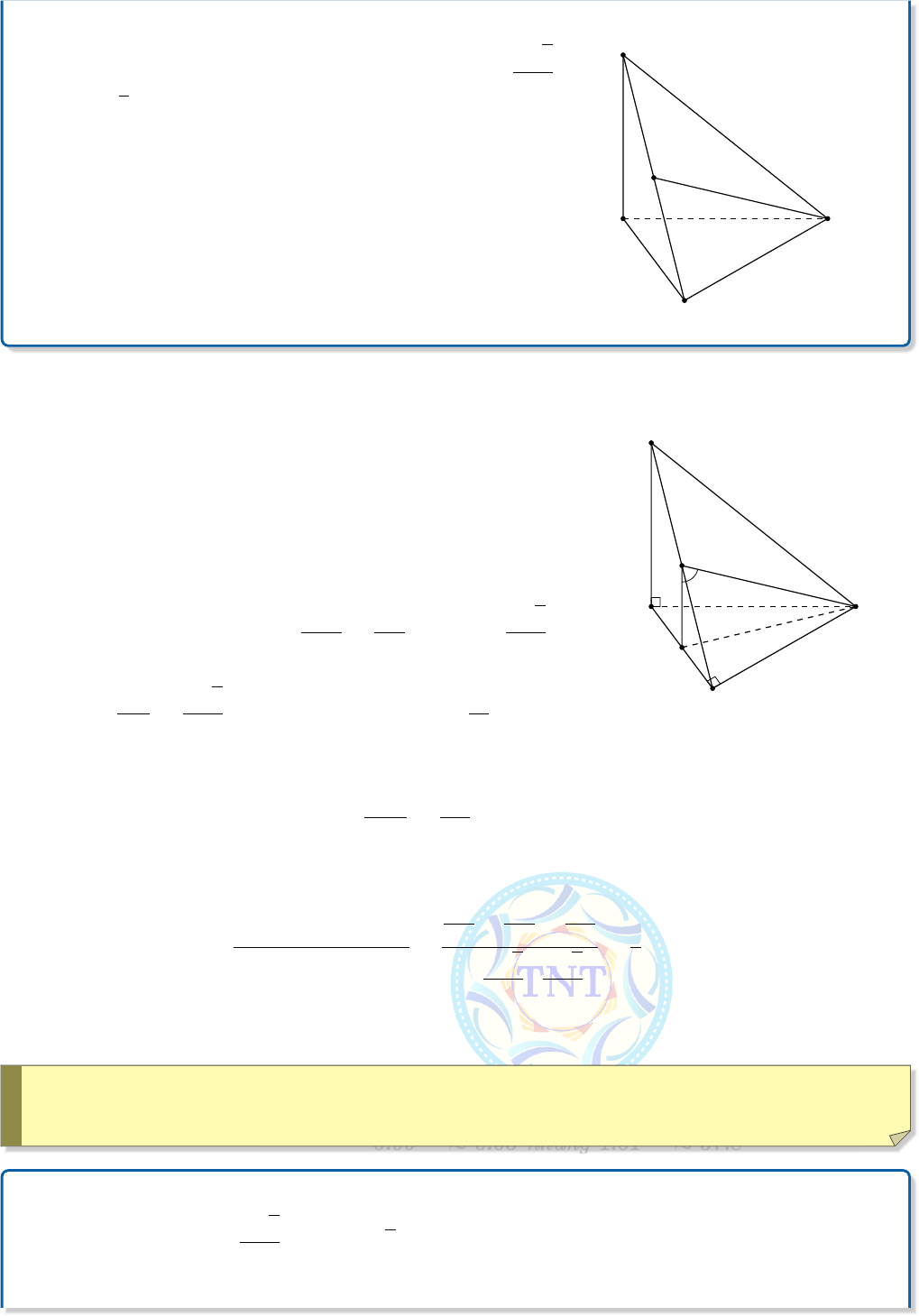
Cho tứ diện ABCD có AB vuông góc với mặt phẳng
(BCD). Biết tam giác BCD vuông tại C và AB =
a
√
6
2
,
AC = a
√
2, CD = a. Gọi E là trung điểm của AC (tham
khảo hình vẽ bên). Góc giữa hai đường thẳng AB và DE
bằng
A. 45
◦
. B. 60
◦
. C. 30
◦
. D. 90
◦
.
B D
E
A
C
Hướng dẫn giải:
Gọi I là trung điểm của BC, suy ra EI k AB.
Khi đó (AB, DE) = (EI, ED) =
[
IED.
Ta có
DC ⊥ BC (giả thiết)
DC ⊥ AB (AB ⊥ (BCD))
⇒ DC ⊥ (ABC),
suy ra DC vuông góc với EC. Do đó
DE
2
= CD
2
+ EC
2
= CD
2
+
AC
2
4
=
3a
2
2
⇒ DE =
a
√
6
2
.
Ta có IE =
AB
2
=
a
√
6
4
và BC
2
= AC
2
− AB
2
=
a
2
2
.
Tam giác ICD vuông tại C nên
DI
2
= CD
2
+ IC
2
= CD
2
+
BC
2
4
=
9a
2
8
.
B D
E
A
C
I
Áp dụng định lý cô-sin cho tam giác IDE, ta có
cos
[
IED =
IE
2
+ DE
2
− CD
2
2IE · DE
=
3a
2
8
+
3a
2
2
−
9a
2
8
2 ·
a
√
6
4
·
a
√
6
2
=
1
2
⇒
[
IED = 60
◦
.
Vậy góc giữa hai đường thẳng AB và DE bằng 60
◦
.
!
Có thể chứng minh EI vuông góc với mặt phẳng (BCD), suy ra tam giác EID vuông tại I để
tính góc
[
IED đơn giản hơn mà không cần sử dụng định lý cô-sin.
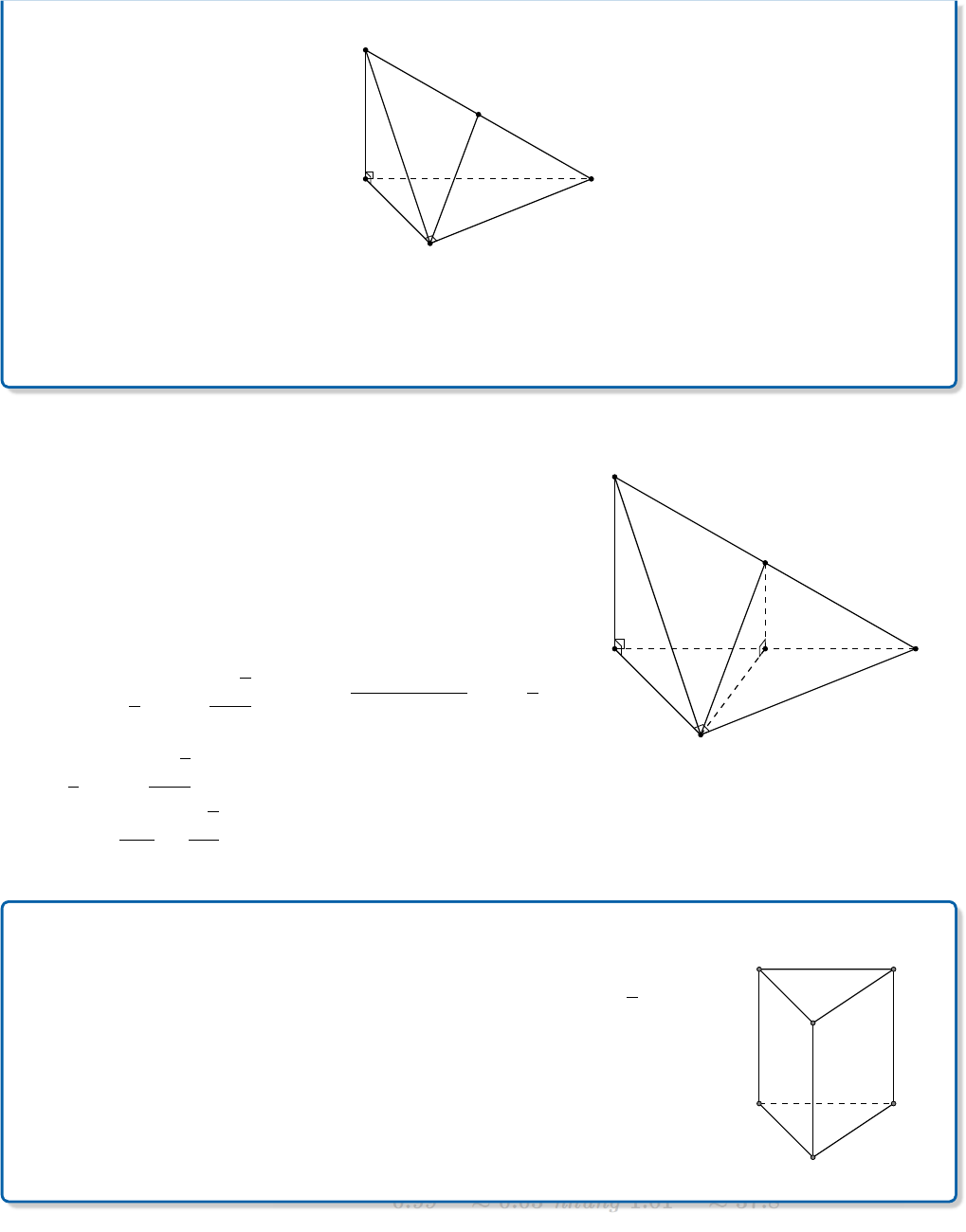
Ví dụ 2. Cho tứ diện ABCD có AB vuông góc với mặt phẳng (BCD). Biết tam giác BCD
vuông tại C và AB =
a
√
6
2
, AC = a
√
2, CD = a. Gọi E là trung điểm của AD (tham khảo
hình vẽ dưới đây).
161 -Bùi Thị Xuân Tp Huế 2 TT Quốc Học Huế
Ð L
A
T
E
X Hóa Nguyễn Hữu Nhanh Tiến h /ToanTienNhanh
B D
E
C
A
Góc giữa hai đường thẳng AB và CE bằng
A. 60
◦
. B. 45
◦
. C. 30
◦
. D. 90
◦
.
Hướng dẫn giải:
Gọi F là trung điểm của BD, suy ra EF k AB nên
(AB, CE) = (EF, CE).
Do AB ⊥ (BCD) nên EF ⊥ (BCD), suy ra 4EF C
vuông tại F .
Mặt khác
CD ⊥ BC
CD ⊥ AB
⇒ CD ⊥ AC.
Ta có EF =
1
2
AB =
a
√
6
4
, AD =
√
AC
2
+ CD
2
= a
√
3.
4ACD vuông tại C và có E là trung điểm của AD nên
CE =
1
2
AD =
a
√
3
2
.
cos
[
CEF =
EF
EC
=
√
2
2
⇒
[
CEF = 45
◦
.
Vậy (AB, CE) = (EF, CE) =
[
CEF = 45
◦
.
B D
E
C
F
A
Ví dụ 3.
Cho hình lăng trụ đứng tam giác ABC.A
0
B
0
C
0
có đáy ABC là tam
giác cân AB = AC = a,
[
BAC = 120
◦
, cạnh bên AA
0
= a
√
2. Tính
góc giữa hai đường thẳng AB
0
và BC (tham khảo hình vẽ bên).
A. 90
◦
. B. 30
◦
. C. 45
◦
. D. 60
◦
.
B
C
B
0
C
0
A
A
0
Hướng dẫn giải:
161 -Bùi Thị Xuân Tp Huế 3 TT Quốc Học Huế
Chia sẻ bởi: 
Trịnh Thị Thanh
Trịnh Thị Thanh Liên kết tải về
Chuyên đề góc và khoảng cách trong không gian 797,7 KB Tải về
Có thể bạn quan tâm
-
Văn mẫu lớp 12: Dàn ý phân tích nhân vật người đàn bà hàng chài (11 Mẫu + Sơ đồ tư duy)
-
Phân tích tác phẩm Giàn bầu trước ngõ của Nguyễn Ngọc Tư
-
Văn mẫu lớp 12: Phân tích nhân vật Trương Ba trong Hồn Trương Ba da hàng thịt
-
Phân tích nhân vật bé Em trong truyện Áo Tết
-
Văn mẫu lớp 12: Phân tích bi kịch của Trương Ba trong tác phẩm Hồn trương ba, da hàng thịt
-
Văn mẫu lớp 12: Nghị luận về ý thức tôn trọng người khác (2 Dàn ý + 14 mẫu)
-
Văn mẫu lớp 9: Phân tích khổ cuối bài Sang thu của Hữu Thỉnh (Sơ đồ tư duy)
-
Văn mẫu lớp 9: Nghị luận ý nghĩa của sự lắng nghe
-
Văn mẫu lớp 12: Tổng hợp mở bài về tác phẩm Chiếc thuyền ngoài xa (71 mẫu)
-
Kể về một việc làm tốt của em (79 mẫu)
Xác thực tài khoản!
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:
Số điện thoại chưa đúng định dạng!
Sắp xếp theo
