Toán 12 Bài 1: Tính đơn điệu của hàm số Giải Toán 12 Cánh diều trang 5 → 14
Giải Toán 12 Bài 1: Tính đơn điệu của hàm số là tài liệu vô cùng hữu ích giúp các em học sinh có thêm nhiều gợi ý tham khảo để giải các bài tập trong SGK Toán 12 Cánh diều tập 1 trang 5, 6, 7, 8, 9, 10, 11, 12, 13, 14.
Giải bài tập Toán 12 Cánh diều tập 1 Bài 1 được trình bày rõ ràng, cẩn thận, dễ hiểu nhằm giúp học sinh nhanh chóng biết cách làm bài. Đồng thời, cũng là tài liệu hữu ích giúp giáo viên thuận tiện trong việc hướng dẫn học sinh ôn tập Bài 1 Chương I: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số. Mời thầy cô và các em theo dõi bài viết dưới đây của Eballsviet.com:
Toán 12 Bài 1: Tính đơn điệu của hàm số
Giải Toán 12 Cánh diều Tập 1 trang 13, 14
Bài 1
Cho hàm số y = f(x) có bảng biến thiên như sau:
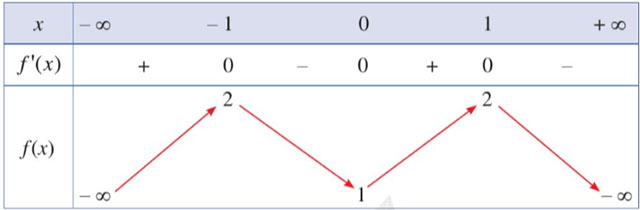
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
|
A. (1; + ∞). B. (– 1; 0). |
C. (– 1; 1). D. (0; 1). |
Đáp số đúng: D
Bài 2
Cho hàm số y = f(x) có bảng biến thiên như sau:
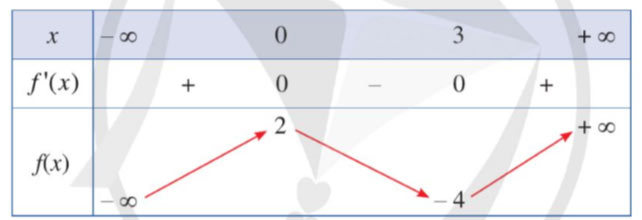
Giá trị cực tiểu của hàm số đã cho bằng
|
A. 2 B. 3 |
C. - 4 D. 0. |
Đáp số đúng: C
Bài 3
Tìm các khoảng đơn điệu của mỗi hàm số sau:
a) y = - x3 + 2x2 - 3;
b) y = x4 + 2x2 + 5;
c) ![]() \(y = \frac{3x+1}{2-x}\);
\(y = \frac{3x+1}{2-x}\);
d) ![]() \(y = \frac{x^{2}-2x }{x+1}\).
\(y = \frac{x^{2}-2x }{x+1}\).
Hướng dẫn giải:
a) y = - x3 + 2x2 - 3
TXĐ: R
Ta có: y' = - 3x2 + 4x;
y' = 0 ⇔ x = 0 hoặc ![]() \(x=\frac{4}{3}\)
\(x=\frac{4}{3}\)
Bảng biến thiên:
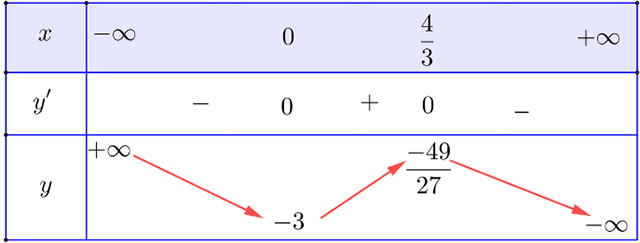
Vậy hàm số nghịch biến trên mỗi khoảng ![]() \((-\infty;0)\) và
\((-\infty;0)\) và ![]() \(\left(\frac{4}{3};+ \infty \right)\); nghịch biến trên khoảng
\(\left(\frac{4}{3};+ \infty \right)\); nghịch biến trên khoảng ![]() \(\left(0;\frac{4}{3}\right)\)
\(\left(0;\frac{4}{3}\right)\)
b) y = x4 + 2x2 + 5
TXĐ: R
Ta có: y' = 4x3 + 4x; y' = 0 ⇔ x = 0
Bảng biến thiên:
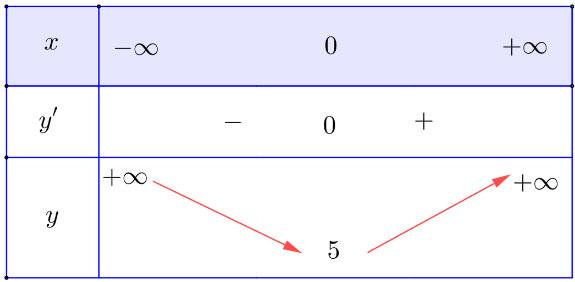
Vậy hàm số nghịch biến trên khoảng (– ∞; 0); đồng biến trên khoảng (0; + ∞).
c) ![]() \(y = \frac{3x+1}{2-x}\)
\(y = \frac{3x+1}{2-x}\)
d) ![]() \(y = \frac{x^{2}-2x }{x+1}\)
\(y = \frac{x^{2}-2x }{x+1}\)
Bài 4
Tìm điểm cực trị của mỗi hàm số sau:
a) y = 2x3 + 3x2 – 36x – 10;
b) y = – x4 – 2x2 + 9;
c) ![]() \(y=x+\frac{1}{x}\)
\(y=x+\frac{1}{x}\)
Hướng dẫn giải:
a) y = 2x3 + 3x2 – 36x – 10
TXĐ: R
Ta có: y' = 6x2 + 6x - 36;
y' = 0 ⇔ x = - 3 hoặc x = 2.
Bảng biến thiên:
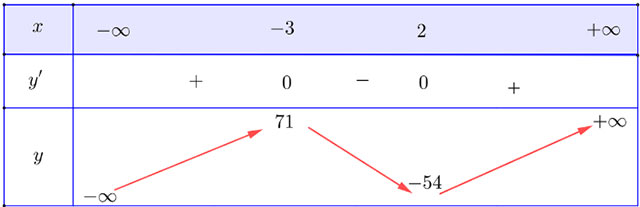
Vậy hàm số đạt cực đại tại x = - 3 và đạt cực tiểu tại x = 2.
b) y = - x4 - 2x2 + 9
TXĐ: R
Ta có: y' = - 4x3 - 4x; y' = 0 ⇔ x = 0
Bảng biến thiên:
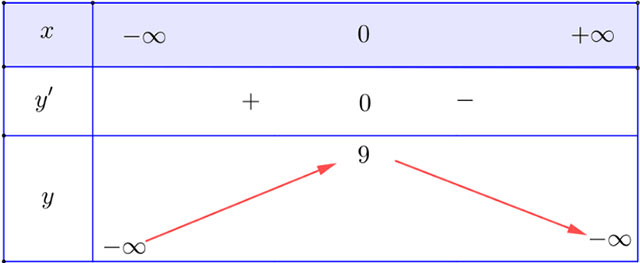
Vậy hàm số đạt cực đại tại x = 0.
c) ![]() \(y=x+\frac{1}{x}\)
\(y=x+\frac{1}{x}\)
Bài 5
Cho hai hàm số y = f(x) = x4 - 2x2 + 2, ![]() \(y=g(x)=-\frac{1}{4}x^4-\frac{1}{3}x^3+x^2-3\) có đồ thị lần lượt được cho ở Hình 6a, Hình 6b. Nêu khoảng đồng biến, nghịch biến và điểm cực trị của mỗi hàm số đó.
\(y=g(x)=-\frac{1}{4}x^4-\frac{1}{3}x^3+x^2-3\) có đồ thị lần lượt được cho ở Hình 6a, Hình 6b. Nêu khoảng đồng biến, nghịch biến và điểm cực trị của mỗi hàm số đó.
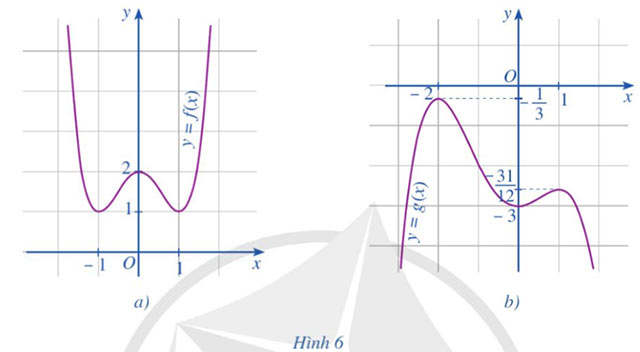
Hướng dẫn giải:
a) y = f(x) = x4 - 2x2 + 2
+ Hàm số y = f(x) đồng biến trên mỗi khoảng (- 1; 0) và (1; + ∞); nghịch biến trên mỗi khoảng (-∞; - 1) và (0; 1).
+ Hàm số đạt cực tiểu tại x = - 1 và x = 1. Hàm số đạt cực đại tại x = 0
b) ![]() \(y=g(x)=-\frac{1}{4}x^4-\frac{1}{3}x^3+x^2-3\)
\(y=g(x)=-\frac{1}{4}x^4-\frac{1}{3}x^3+x^2-3\)
+ Hàm số y = f(x) nghịch biến trên mỗi khoảng (- 2; 0) và (1; + ∞); đồng biến trên mỗi khoảng (- ∞; - 2) và (0; 1).
+ Hàm số đạt cực tiểu tại x = 0. Hàm số đạt cực đại tại x = - 2 và x = 1.
Bài 6
Thể tích V (đơn vị: cm3) của 1 kg nước tại nhiệt độ T (đơn vị oC) với 0 ≤ T ≤ 30 được tính bởi công thức sau:
V(T) = 999,87 – 0,06426T + 0,0085043T2 – 0,0000679T3.
(Nguồn: J. Stewart, Calculus, Seventh Edition, Brooks/Cole, CENGAGE Learning 2012)
Hỏi thể tích V(T), 0 ≤ T ≤ 30, giảm trong khoảng nhiệt độ nào?
Hướng dẫn giải:
Xét hàm số y = V(T) = 999,87 – 0,06426T + 0,0085043T2 – 0,0000679T3
Ta có: y' = - 0,0002037T2 + 0,0170086T - 0,06426
y' = 0 ⇔ T = 3,966 (vì 0 ≤ T ≤ 30)
Bảng biến thiên của hàm số y = V(T):

Vậy thể tích V(T), 0 ≤ T ≤ 30, giảm trong khoảng (0; 3,996)
Bài 7
Kính viễn vọng không gian Hubble được đưa vào vũ trụ ngày 24/4/1990 bằng tàu con thoi Discovery. Vận tốc của tàu con thoi trong sứ mệnh này, từ lúc cất cánh tại thời điểm t = 0 (s) cho đến khi tên lửa đẩy được phóng đi tại thời điểm t = 126 (s), cho bởi hàm số sau:
v(t) = 0,001302t3 – 0,09029t2 + 23,
(v được tính bằng ft/s, 1 feet = 0,3048 m)
(Nguồn: J. Stewart, Calculus, Seventh Edition, Brooks/Cole, CENGAGE Learning 2012)

Hỏi gia tốc của tàu con thoi sẽ tăng trong khoảng thời gian nào tính từ thời điểm cất cánh cho đến khi tên lửa đẩy được phóng đi?
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:












 Đề thi học kì 1 Lớp 12
Đề thi học kì 1 Lớp 12
 Đề thi giữa học kì 1 Lớp 12
Đề thi giữa học kì 1 Lớp 12
 Đề thi giữa học kì 2 Lớp 12
Đề thi giữa học kì 2 Lớp 12
 Đề thi học kì 2 Lớp 12
Đề thi học kì 2 Lớp 12
 Soạn Văn 12 KNTT
Soạn Văn 12 KNTT
 Soạn Văn 12 CTST
Soạn Văn 12 CTST
 Soạn Văn 12 Cánh Diều
Soạn Văn 12 Cánh Diều
 Văn 12
Văn 12
 Toán 12 Chân trời sáng tạo
Toán 12 Chân trời sáng tạo









