Phương pháp giải nhanh mặt cầu ngoại tiếp hình chóp Tài liệu ôn tập môn Toán lớp 12
Với mong muốn đem đến cho các bạn có thêm nhiều tài liệu học tập, giải nhanh toán học lớp 12 Downoad.com.vn giới thiệu tài liệu Phương pháp giải nhanh mặt cầu ngoại tiếp hình chóp.
Phương pháp giải nhanh bài toán mặt cầu ngoại tiếp hình chóp là tài liệu hữu ích, với các công thức giải nhanh kèm theo ví dụ minh họa và 27 bài toán trắc nghiệm áp dụng. Hy vọng với tài liệu này các bạn học sinh lớp 12 có thêm nhiều tài liệu tham khảo, củng cố kiến thức để đạt được kết quả cao trong các bài kiểm tra, bài thi THPT Quốc gia sắp tới. Mời các bạn cùng tham khảo trong bài viết dưới đây.
Phương pháp giải nhanh mặt cầu ngoại tiếp hình chóp
GV : Hoàng Trọng Tấn , Tân Phú , TPHCM Tel : 0909520755 ,
Face : Hoàng Trọng Tấn Page : Trắc Nghiệm Toán
PP tính nhanh bán kính mặt cầu ngoại tiếp các loại
Loại 1 : Hình chóp có các đỉnh nhìn đoạn thẳng nối 2 đỉnh còn lại dưới 1 góc vuông.
Gọi d là độ dài đoạn thẳng trên thì ta có bán kính mặt cầu ngoại tiếp là:
2
d
R
Ví dụ : Cho hình chóp SABC có tam giác ABC vuông tại B , SA vuông góc với mặt
phẳng (ABC) và SC=2a . Tính diện tích và thể tích mặt cầu ngoài tiếp hình chóp trên
Giải :
Dễ thấy tam giác SAC vuông tại A , tam giác SBC vuông tại B từ đó hình chóp này loại
1 nên
2
22
SC a
Ra
Ví dụ : Cho hình chóp SABCD có đáy ABCD là hình vuông , SA vuông góc với mặt
phẳng (ABCD) và SC=2a . Tính diện tích và thể tích mặt cầu ngoài tiếp hình chóp trên
Giải :
Dễ thấy tam giác SAC vuông tại A , tam giác SBC vuông tại B và giác SDC vuông tại D
từ đó hình chóp này loại 1 nên :
2
22
SC a
Ra
Loại 2 : Hình chóp đều
GV : Hoàng Trọng Tấn , Tân Phú , TPHCM Tel : 0909520755 ,
Face : Hoàng Trọng Tấn Page : Trắc Nghiệm Toán
Gọi h là độ cao hình chóp và k là chiều dài cạnh bên thì ta có bán kính mặt cầu là :
2
2
k
R
h
Ví dụ : Cho hình chóp tam giác đều S.ABC , có AB=a và cạnh bên SA=2a , tính diện tích
và thể tích mặt cầu ngoại tiếp hình chóp trên
Giải : gọi G là trọng tâm tam giác thì ta có SG vuông góc với mặt phẳng (ABC)
Thế thì
,SG hSA k
nên R mặt cầu :
2
2
SA
R
SG
2
22
2
SA
R
S AGA
2
2
2
2 33
11
3
2
3
SA
Ra
SA AB
Ví dụ: Cho hình chóp tứ giác đều S.ABCD , có AB=a và cạnh bên SA=2a , tính diện tích
và thể tích mặt cầu ngoại tiếp hình chóp trên
Giải : gọi O là tâm hình vuông ABCD thì ta có SO vuông góc với mặt phẳng (ABCD)
Thế thì
,SO hSA k
nên R mặt cầu :
2
2
SA
R
SO
2
22
2
SA
R
S AOA
2
2
2
2 14
7
2
2
2
SA
Ra
AB
SA
Loại 3 : Hình chóp có cạnh bên vuông góc với đáy
GV : Hoàng Trọng Tấn , Tân Phú , TPHCM Tel : 0909520755 ,
Face : Hoàng Trọng Tấn Page : Trắc Nghiệm Toán
Gọi h là chiều cao hình chóp và
d
R
là bán kính của đáy thì bán kính mặt cầu :
2
2
2
d
h
RR
Ví dụ : cho hình chóp SABCD có cạnh SA vuông góc với đáy , ABCD là hình chữ nhật
có đường chéo dài
5a
, SA=2a . Tính diện tích và thể tích mặt cầu ngoại tiếp SABCD
Giải : Ta có :
2
day
AC
R
và SA=hÁp dụng công thức ta có :
22
22
SAAC
R
2
2
5 21
22
2aaa
R
a
Ví dụ : cho hình chóp SABC có cạnh SA vuông góc với đáy , ABC là tam giác đều cạnh =
a , SA dài 2a . Tính diện tích và thể tích mặt cầu ngoại tiếp SABCD
Giải : Ta có
2 2 3 3
.
3 3 2 3
day
R AM AB AB
và SA=h
Áp dụng công thức ta có :
2
2
23
26
SA
R AB
3
3
a
R
Ví dụ : cho hình chóp SABC có cạnh SA vuông góc với đáy , ABC là tam giác vuông tại
A và BC=2a , SA dài 2a . Tính diện tích và thể tích mặt cầu ngoại tiếp SABCD
Giải : Ta có
2
day
BC
R
và SA=h .Áp dụng công thức ta có :
22
2
2
2
SABC
R R a
Ví dụ : cho hình chóp SABC có cạnh SA vuông góc với đáy , ABC là tam giác cân tại A
và AB=a và góc A =120 độ , SA dài 2a . Tính diện tích và thể tích mặt cầu ngoại tiếp
SABC
Chia sẻ bởi: 
Trịnh Thị Thanh
Trịnh Thị Thanh Liên kết tải về
Phương pháp giải nhanh mặt cầu ngoại tiếp hình chóp 467,4 KB Tải về
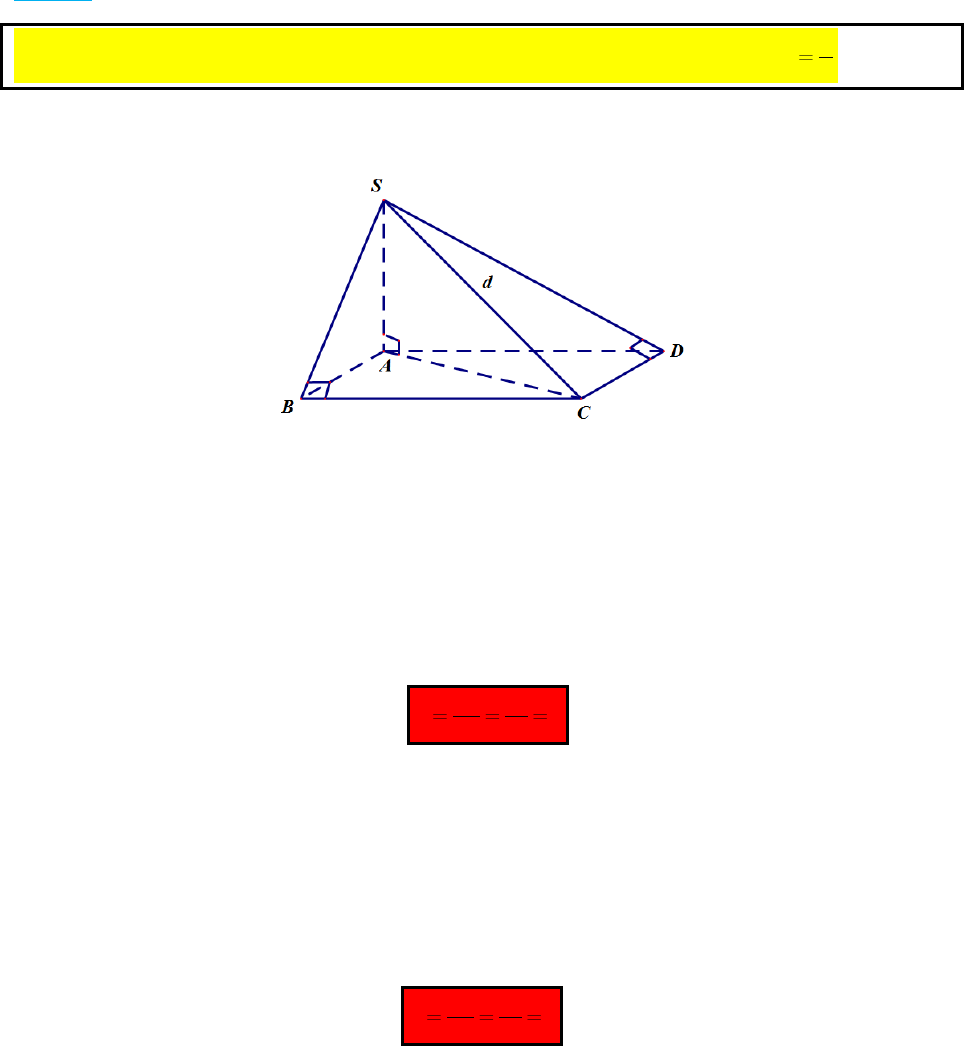
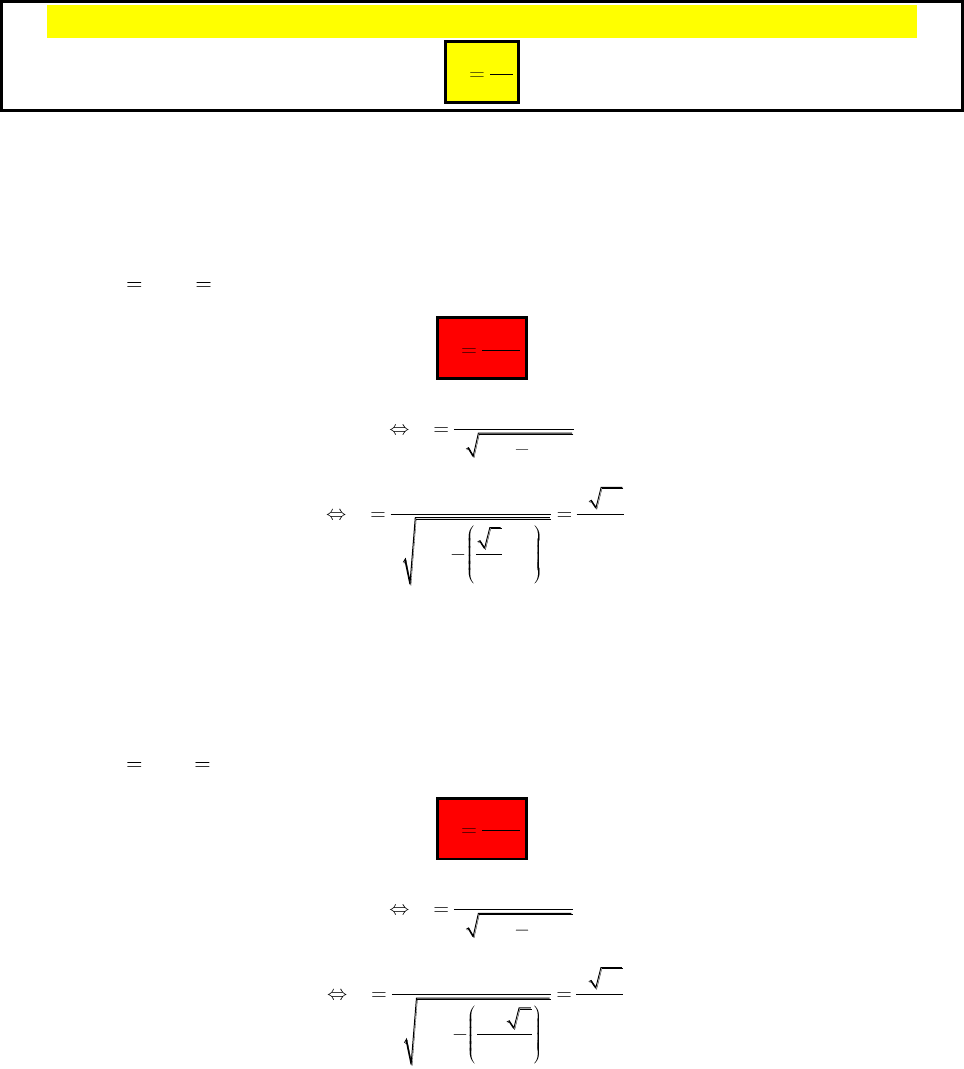
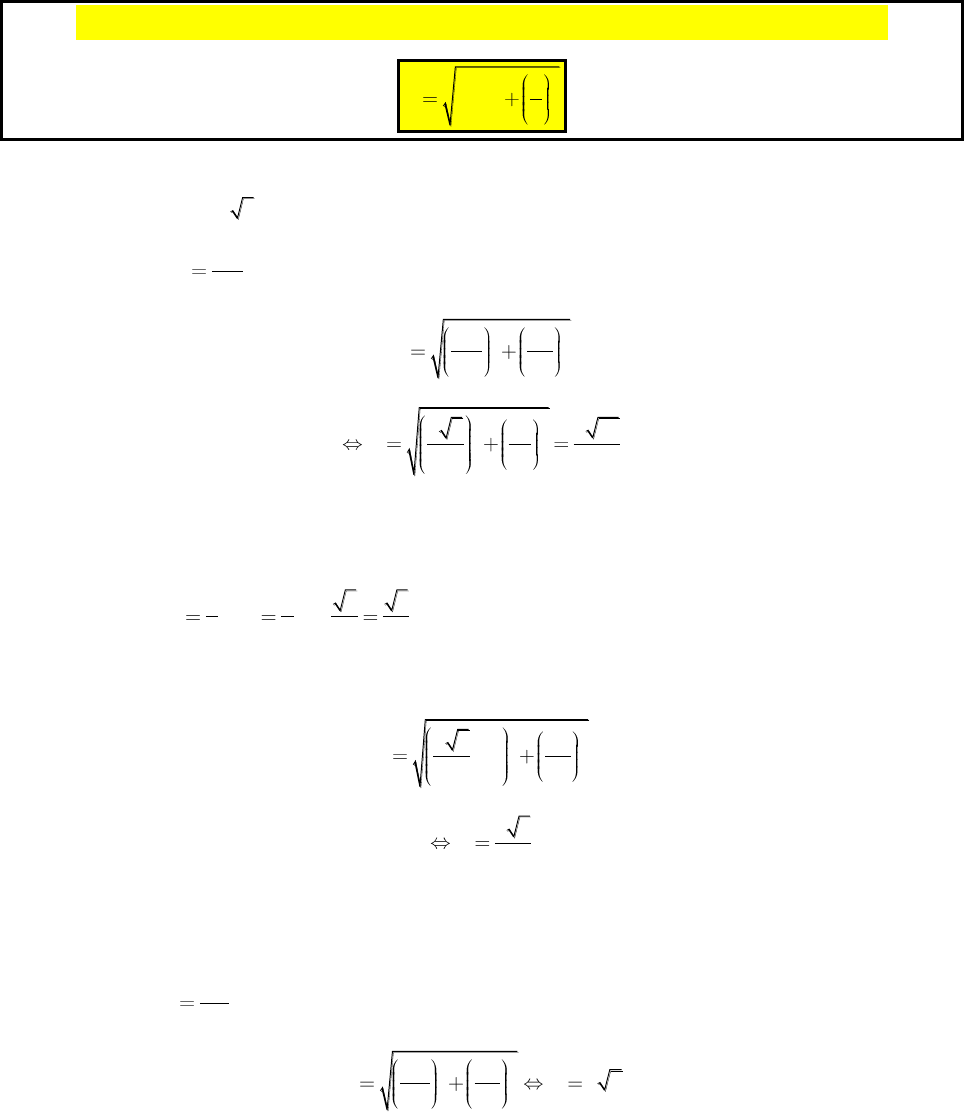
Có thể bạn quan tâm
-
Văn mẫu lớp 12: Dàn ý phân tích nhân vật người đàn bà hàng chài (11 Mẫu + Sơ đồ tư duy)
-
Phân tích tác phẩm Giàn bầu trước ngõ của Nguyễn Ngọc Tư
-
Văn mẫu lớp 12: Phân tích nhân vật Trương Ba trong Hồn Trương Ba da hàng thịt
-
Phân tích nhân vật bé Em trong truyện Áo Tết
-
Văn mẫu lớp 12: Phân tích bi kịch của Trương Ba trong tác phẩm Hồn trương ba, da hàng thịt
-
Văn mẫu lớp 12: Nghị luận về ý thức tôn trọng người khác (2 Dàn ý + 14 mẫu)
-
Văn mẫu lớp 9: Phân tích khổ cuối bài Sang thu của Hữu Thỉnh (Sơ đồ tư duy)
-
Văn mẫu lớp 9: Nghị luận ý nghĩa của sự lắng nghe
-
Văn mẫu lớp 12: Tổng hợp mở bài về tác phẩm Chiếc thuyền ngoài xa (71 mẫu)
-
Kể về một việc làm tốt của em (79 mẫu)
Xác thực tài khoản!
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:
Số điện thoại chưa đúng định dạng!
Sắp xếp theo
