Giao thoa sóng: Định nghĩa, công thức và bài tập Tài liệu ôn tập Vật lí 12
Giao thoa sóng là sự tổng hợp của hai sóng kết hợp trong không gian, trong đó có những chỗ biên độ sóng được tăng cường hay bị giảm bớt.
Trong bài viết dưới đây Eballsviet.com xin giới thiệu đến quý thầy cô cùng các em học sinh tài liệu Tổng hợp kiến thức về Giao thoa sóng được chúng tôi tổng hợp chi tiết, chính xác nhất. Đây là tài liệu tổng hợp toàn bộ kiến thức về giao thoa sóng như: khái niệm, hiện tượng, công thức và bài tập. Qua đó giúp các em nắm vững được kiến thức trọng tậm của môn Vật lý lớp 12.
Tổng hợp kiến thức về Giao thoa sóng
I. Khái niệm giao thoa sóng
Giao thoa sóng là sự tổng hợp của hai sóng kết hợp trong không gian, trong đó có những chỗ biên độ sóng được tăng cường hay bị giảm bớt.
* Điều kiện để có giao thoa: Do hai nguồn kết hợp tạo ra. Hai nguồn kết hợp là hai nguồn có cùng tần số và có hiệu số pha không đổi theo thời gian.
II. Hiện tượng giao thoa sóng
Quan sát hiện tượng giao thoa sóng trên mặt nước, ta quan sát thấy:
- Trong vùng gặp nhau (vùng giao thoa của hai sóng) xuất hiện những điểm mà tại đó nước dao động mạnh và những điểm mà tại đó nước yên lặng (đứng yên không dao động).
-Hiện đó gọi là hiện tượng giao thoa ánh sáng. Các gợn sóng có hình các đường hypebol gọi là các vân giao thoa.
III. Công thức giao thoa sóng
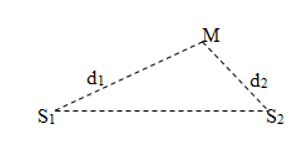
Khảo sát sự giao thoa của hai sóng phát ra từ hai nguồn sóng kết hợp S1, S2 cùng biên độ A.
Xét điểm M cách hai nguồn lần lượt d1, d2
Phương trình sóng tại 2 nguồn:
u1 = Acos(2πft + Φ1) và u2 = Acos(2πft + Φ2)
Phương trình sóng tại M do hai sóng từ hai nguồn truyền tới:
\(\begin{aligned} u_{1 M} &=A \cos \left(2 \pi f t+\varphi_{1}-2 \pi \frac{d_{1}}{\lambda}\right) \\ \text { và } u_{2 M} &=A \cos \left(2 \pi f t+\varphi_{2}-2 \pi \frac{d_{2}}{\lambda}\right) \end{aligned}\)
Phương trình giao thoa sóng tại M:\(\mathrm{u}_{\mathrm{M}}=\mathrm{u}_{1 \mathrm{M}}+\mathrm{u}_{2 \mathrm{M}}\)\(=2 \mathrm{~A} \cos \left[\pi \frac{\mathrm{d}_{2}-\mathrm{d}_{1}}{\lambda}-\frac{\Delta \varphi}{2}\right] \cos \left[2 \pi \mathrm{ft}-\pi \frac{\mathrm{d}_{1}+\mathrm{d}_{2}}{\lambda}+\frac{\varphi_{1}+\varphi_{2}}{2}\right]\)
1) Biên độ dao động tại \(\mathrm{M}: \mathrm{A}_{\mathrm{M}}=2 \mathrm{~A} \mid \cos \left(\pi \frac{\mathrm{d}_{2}-\mathrm{d}_{1}}{\lambda}-\frac{\Delta \varphi}{2}\right) với \Delta \varphi=\varphi_{2}-\varphi 1.\)
Những điểm có biên độ cực đại: AM = 2A
\(\Leftrightarrow \cos \left(\pi \frac{\mathrm{d}_{2}-\mathrm{d}_{1}}{\lambda}-\frac{\Delta \varphi}{2}\right)=\pm 1\)
\(\Leftrightarrow \mathrm{d}_{2}-\mathrm{d}_{1}=\left(\mathrm{k}+\frac{\varphi_{2}-\varphi_{1}}{2 \pi}\right) \lambda\)
(2 sóng từ 2 nguôn cùng pha nhau tại M
Những điểm có biên độ cực tiểu:
\(\Leftrightarrow \cos \left(\pi \frac{\mathrm{d}_{2}-\mathrm{d}_{1}}{\lambda}-\frac{\Delta \varphi}{2}\right)=0\)
\(\Leftrightarrow \mathrm{d}_{2}-\mathrm{d}_{1}=\left(\mathrm{k}+\frac{\varphi_{2}-\varphi_{1}}{2 \pi}+\frac{1}{2}\right) \lambda\)
(2 sóng từ 2 nguồn ngược pha nhau tại M)
(k = 0, ± 1, ± 2,… là thứ tự các tập hợp điểm đứng yên kể từ Mo , k = 0 là tập hợp điểm đứng yên thứ 1)
2) Hai nguồn dao động cùng pha (∆φ = φ2 – φ1 = 0 hoặc = 2kπ).
Thay φ1 = φ2 = φ vào các phương trình trên ta được:
*Phương trình giao thoa sóng tại M:
\(\mathrm{u}_{\mathrm{M}}=\mathrm{u}_{1 \mathrm{M}}+\mathrm{u}_{2 \mathrm{M}}=2 \mathrm{~A} \cos \left(\pi \frac{\mathrm{d}_{2}-\mathrm{d}_{1}}{\lambda}\right) \cos \left(2 \pi \mathrm{ft}-\pi \frac{\mathrm{d}_{1}+\mathrm{d}_{2}}{\lambda}+\varphi\right)\)
* Biên độ sóng tổng hợp:
+ AM max = 2A khi: Hai sóng thành phần tại M cùng pha nhau ∆ φM1/M2 = 2kπ (k∈Z).
Khi đó hiệu đường đi: ∆d = d2 – d1 = kλ
+ AM min = 0 khi:
- Hai sóng thành phần tại M ngược pha nhau ∆ φM1/M2 = (2k + 1)π (k ∈ Z).
- Hiệu đường đi: ∆d = d2 – d1 = (k + 1/2 )λ.
* Tìm số điểm dao động cực đại trên đoạn S1S2: d1 – d2 = kλ (k ∈ Z);
Số điểm cực đại: -S1S2/λ ≤ k ≤ S1S2/λ
* Tìm số điểm dao động cực tiểu trên đoạn S1S2: d1 – d2 = (2k + 1)λ/2 (k ∈ Z)
Số điểm cực tiểu: -S1S2/λ - 1/2 ≤ k ≤ S1S2/λ - 1/2
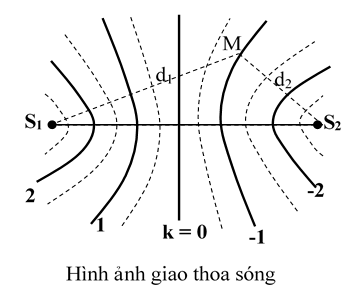Khi hai nguồn dao động cùng pha và cùng biên độ A thì trung điểm của S1S2 có biên độ cực đại Amax = 2A và tập hợp các điểm cực tiểu và cực đại là họ các đường Hypecbol có S1, S2 là tiêu điểm.
3) Hai nguồn dao động ngược pha: \(\left(\Delta \varphi=\varphi_{2}-\varphi_{1}=\pi\right)\)
* Phương trình giao thoa sóng tại M:
\(\mathrm{u}_{\mathrm{M}}=\mathrm{u}_{1 \mathrm{M}}+\mathrm{u}_{2 \mathrm{M}}=2 \mathrm{Acos}\left(\pi \frac{\mathrm{d}_{2}-\mathrm{d}_{1}}{\lambda}-\pi\right) \cos \left(2 \pi \mathrm{ft}-\pi \frac{\mathrm{d}_{1}+\mathrm{d}_{2}}{\lambda}+\frac{\varphi_{1}+\varphi_{2}}{2}\right)\)
* Biên độ sóng tổng hợp: \(\mathrm{A}_{\mathrm{M}}=2 \mathrm{~A} \mid \cos \left(\pi \frac{\mathrm{d}_{2}-\mathrm{d}_{1}}{\lambda}-\pi\right)\)
*Điểm dao động cực đại: \(\mathrm{d}_{2}-\mathrm{d}_{1}=(\mathrm{k}+1 / 2) \lambda(\mathrm{k} \in \mathrm{Z})\)
Số đường hoặc số điểm dao động cực đại (không tính hai nguồn) trên đoạn S1S2:
-S1S2/λ - 1/2 ≤ k ≤ S1S2/λ - 1/2
* Điểm dao động cực tiểu (không dao động):
d2 – d1 = kl (k∈Z)
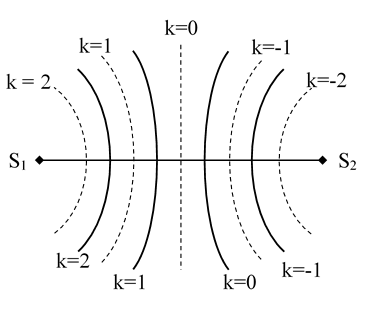
Số đường hoặc số điểm dao động cực tiểu (không tính hai nguồn) trên đoạn S1S2:
-S1S2/λ ≤ k ≤ S1S2/λ
Vậy khi hai nguồn dao động cùng biên độ A và ngược pha thì trung điểm của S1S2 có biên độ cực tiểu Amin = 0.
4. Trường hợp hai nguồn dao động vuông pha nhau: (∆φ = φ2 – φ1 = π/2)
*Phương trình giao thoa sóng tại M:
\(\mathrm{u}_{\mathrm{M}}=\mathrm{u}_{1 \mathrm{M}}+\mathrm{u}_{2 \mathrm{M}}=2 \mathrm{~A} \cos \left(\pi \frac{\mathrm{d}_{2}-\mathrm{d}_{1}}{\lambda}-\frac{\pi}{4}\right) \cos \left(2 \pi \mathrm{ft}-\pi \frac{\mathrm{d}_{1}+\mathrm{d}_{2}}{\lambda}+\frac{\varphi_{1}+\varphi_{2}}{2}\right)\)
* Biên độ sóng tổng hợp:\(\mathrm{A}_{\mathrm{M}}=2 \mathrm{~A} \mid \cos \left(\pi \frac{\mathrm{d}_{2}-\mathrm{d}_{1}}{\lambda}-\frac{\pi}{4}\right)\)
* Điểm dao động cực đại: d2 – d1 = (k + 1/4)λ (k∈Z)
Số đường hoặc số điểm dao động cực đại trên đoạn S1S2:
-S1S2/λ - 1/4 ≤ k ≤ S1S2/λ - 1/4
* Điểm dao động cực tiểu (không dao động): d2 – d1 = (k + 3/4)λ (k∈Z)
Số đường hoặc số điểm dao động cực tiểu trên đoạn S1S2:
-S1S2/λ - 3/4 ≤ k ≤ S1S2/λ - 3/4
Vậy khi hai nguồn dao động cùng biên độ A và vuông pha thì trung điểm của S1S2 có biên độ bằng AM = A√2 .
5. Trường hợp tổng quát: Hai nguồn cùng tần số, khác biên độ, khác pha ban đầu.
Phương trình sóng tại 2 nguồn:
u1 = A1cos(2πft + φ1) và u2 = A2cos(2πft + φ2)
Phương trình sóng tại M do hai sóng từ hai nguồn truyền tới:
\(\begin{aligned} u_{1 \mathrm{M}} &=\mathrm{A}_{1} \cos \left(2 \pi \mathrm{ft}+\varphi_{1}-2 \pi \frac{\mathrm{d}_{1}}{\lambda}\right) \\ \text { và } \mathrm{u}_{2 \mathrm{M}} &=\mathrm{A}_{2} \cos \left(2 \pi \mathrm{ft}+\varphi_{2}-2 \pi \frac{\mathrm{d}_{2}}{\lambda}\right) \end{aligned}\)
* Phương trình giao thoa sóng tại M:
Sử dụng phương pháp tổng hợp hai dao động điều hòa bằng vectơ quay, ta xác định được:
uM = u1M + u2M = AM cos (2πft + φM)
Trong đó: \(\mathrm{A}_{\mathrm{M}}=\sqrt{\mathrm{A}_{1}^{2}+\mathrm{A}_{2}^{2}+2 \mathrm{~A}_{1} \mathrm{~A}_{2} \cos \Delta \varphi}\)
∆φ là độ lệch pha của hai dao động sóng tới tại M: ∆φ = φ2 - φ1 = 2π. (d2-d1)/λ
→ │A1 – A2│ ≤ AM ≤ A1 + A2
+ Điểm M dao động với biên độ cực đại AM = A1 + A2 khi và chỉ khi dao động sóng từ hai nguồn tới M đồng pha với nhau: ∆φ = 2kπ
\(\Leftrightarrow \mathrm{d}_{2}-\mathrm{d}_{1}=\left(\mathrm{k}+\frac{\varphi_{2}-\varphi_{1}}{2 \pi}+\frac{1}{2}\right) \lambda\)
+ Điểm M dao động với biên độ cực tiểu AM = │A1 – A2│ khi và chỉ khi dao động sóng từ hai nguồn tới M ngược pha với nhau: ∆φ = (2k + 1)π
\(\Leftrightarrow \mathrm{d}_{2}-\mathrm{d}_{1}=\left(\mathrm{k}+\frac{\varphi_{2}-\varphi_{1}}{2 \pi}+\frac{1}{2}\right) \lambda\)
+ Tổng quát: Điểm M dao động với biên độ bất kỳ AM khi và chỉ khi dao động sóng từ hai nguồn tới M lệch pha với nhau: ∆φ = ± α + 2kπ với α thỏa mãn
\(\Leftrightarrow \mathrm{d}_{2}-\mathrm{d}_{1}=\left(\mathrm{k}+\frac{\varphi_{2}-\varphi_{1}}{2 \pi} \mp \frac{\alpha}{2 \pi}\right) \lambda\)
IV. Một số dạng bài tập giao thoa sóng
Dạng 1: Xác định các đặc trưng của sóng và các điểm nằm trong miền giao thoa
Đối với dạng bài tập này em cần ôn luyện nhiều để hiểu về hết nội dung về giao thoa sóng là gì?
Bài tập 1: Tại 2 điểm A và B trên mặt nước có hai nguồn sóng giống nhau với biên độ a, bước sóng là 6cm. Điểm N nằm trên cực tiểu thứ 5 tính từ trung điểm của AB, khoảng cách NA và NB có thể là:
A. NA = 15cm và NB = 39 cm
B. NA = 18 cm và NB = 24 cm
C. NA = 40 cm và NB = 24 cm
D. NA = 49 cm và NB = 22cm
Đáp án: D
Bài tập 2: Tại 2 điểm A và B trên mặt nước có hai nguồn sóng kết hợp ngược pha, bước sóng là 12 cm. Điểm M và N có 4 đường cực đại, khoảng cách giữa 2 điểm M và N là:
A. 21 cm
B. 24 cm
C. 27 cm
D. 30 cm
Đáp án B
Dạng 2: Bài tập giao thoa sóng là gì? Xác định số điểm cực đại, cực tiểu
Bài tập 1: Tại 2 điểm trên mặt nước, có hai nguồn phát sóng A và B có phương trình u = asin(40Πt) cm, vận tốc truyền sóng là 50cm/s. A và B cách nhau 11 cm. Gọi M là điểm trên mặt nước có MA = 10cm và MB = 5cm. Số điểm dao động cực đại trên đoạn AM là:
A. 9
B. 7
C. 2
D.6
Đáp án: B
Bài tập 2: Hai nguồn kết hợp A, B cách nhau 16 cm dao động cùng pha. C là điểm nằm trên đường dao động cực tiểu. Giữa đường cực tiểu qua C và trung trực của AB còn có một đường dao động cực đại. Biết rằng AC = 17,2 cm; BC = 13,6 cm. Số đường dao động cực đại trên AC là:
A. 16
B. 6
C.5
D.8
Đáp án: D
Dạng 3: Bài toán về vị trí các điểm cực đại, cực tiểu
Bài tập 1: Dùng một âm thoa có tần số rung ƒ = 100 Hz. Người ta tạo ra tại hai điểm A, B trên mặt nước hai nguồn sóng có cùng biên độ, cùng pha. Biết AB = 3,2cm, tốc độ truyền sóng là v = 40cm/s. Gọi I là trung điểm của AB. Tính khoảng cách từ I đến điểm M gần I nhất dao động cùng pha với I và nằm trên trung trực của AB?
A. 1,8 cm
B. 1,3 cm
C. 1,2 cm
D. 1,1 cm
Đáp án: C
Bài tập 2: Giao thoa sóng nước với hai nguồn giống hệt nhau A và B cách nhau 20 cm có tần số 50 Hz. Tốc độ truyền sóng trên mặt nước là 1,5m/s. Trên mặt nước xét đường tròn tâm A, bán kính AB. Điểm trên đường tròn dao động với biên độ cực đại cách đường thẳng qua A, B một đoạn gần nhất là:
A. 18,67 mm
B. 17,96 mm
C. 19, 97mm
D.15,34 mm
Đáp án C
Dạng 4: Bài toán về độ lệch pha của các điểm trên đường trung trực
Bài tập: Trong thí nghiệm giao thoa sóng nước, hai nguồn kết hợp A và B đặt cách nhau 10cm dao động cùng pha. Sóng tạo ra trên mặt nước có bước sóng 1,5cm. Trong miền giao thoa xét 2 điểm M, N nằm trên đường trung trực của AB và cùng cách trung điểm I của đoạn AB một đoạn 12cm. Số điểm dao động cùng pha với nguồn trên đoạn MN là:
A.9
B.10
C. 11
D.12
Đáp án: B
V. Bài tập giao thoa sóng
Câu 1: cho hai nguồn kết hợp cùng pha cách nhau 10cm, bước sóng 3cm. Điểm M nằm trên đường tròn đường kính AB, không thuộc đường trung trực, dao động cực đại và nằm gần đường trung trực nhất. Khoảng cách từ M đến A lớn nhất và bé nhất là?
A; 5,41cm 2,34cm
B; 8,41cm 5,41cm
C; 8,41cm 2,34cm
D; đáp án khác
Câu 2: hai nguồn kết hợp ngược pha cách nhau 10cm, bước sóng 3cm. Điểm M thuộc đường tròn đường kính AB, không thuộc đường trung trực , dao động cực đại và xa đường trung trực của AB nhất. M cách B molotj khoảng lớn nhất và nhỏ nhất bao nhiêu?
A; 9,74cm 2,24cm
B; 6,32cm 1,22cm
C; 9,74cm 1,24cm
D; đáp án khác
Câu 3: cho hai nguồn kết hợp v=10cm/s cách nhau 5cm. Điểm M nằm trên đường tròn đường kính AB, không thuộc đường trung trực, dao động cực đại và nằm gần đường trung trực nhất. Khoảng cách từ M đến A lớn nhất và bé nhất là?
A; 2,62cm 1,24cm
B; 3,66cm 1,26cm
C; 3,66cm 3,14c
D; đáp án khác
Câu 4: cho hai nguồn kết hợp ngược pha nhau cách nhau 11cm bước sóng 2,5cm. Xét các điểm dao động cực đại trên đường tròn tâm A bán kính AB:Khoảng cách từ điểm đó đến B lớn nhất và bé nhất là bao nhiêu:?
A; 9,75cm 2,25cm
B; 9,75cm 1,35cm
C; 1,35cm 2,25cm
D; đáp án khác
Khoảng cách từ điểm đó đến đường trung trực của AB bé nhất và lớn nhất là bao nhiêu?
A; 1,179cm 23,11cm
B; 1,179cm 12,23cm
C; 12,23cm 23,11cm
D; Đáp án khác
Câu 5: cho hai nguồn kết hợp,v=20cm/s cách nhau 21,8cm. Xét các điểm dao động cực tiểu trên đường tròn tâm B bán kính AB:Khoảng cách từ điểm đó đến A lớn nhất và bé nhất là bao nhiêu:?
A: 22,53cm 1,27cm
B;40,97cm 0,97cm
C;40,97cm 1,27cm
D; đáp án khác
Câu 6. Hai điểm M, N trên mặt chất lỏng cách hai nguồn cùng pha S1, S2 những đoạn lần lượt là: S1M = 3,25cm, S1N = 33cm , S2M = 9,25cm , S2N = 67cm, hai nguồn dao động cùng tần số 20HZ , vận tốc truyền sóng 80cm/s. Hai điểm này dao động:
A. M không dao động, N dao động mạnh nhất.
B. M dao động mạnh nhất, N không dao động.
C. Cả M và N đều dao động mạnh nhất.
D. Cả M và N đều không dao động.
Câu 7: Hai nguồn sóng kết hợp A và B cách nhau 13cm dao động ngược pha . Điểm cực tiểu M có MA - MB= 3cm. Giữa M và đường trung trực của AB có 2 đường cực đại Số điểm dao động với biên độ cực đại giữa A và B là
A. 2
B. 18
C. 21
D. 17
Câu 8: Hai nguồn sóng kết hợp A và B cách nhau 11cm dao động ngược pha . Điểm cực đại M có MA - MB= 5cm. Giữa M và đường trung trực của AB có 2 đường cực tiểu Số điểm dao động với biên độ cực triểu giữa A và B là :
A. 11
B. 9
C. 12
D. 10
Câu 9:Hai nguồn sóng kết hợp S1 và S2 cách nhau 13cm có phương trình sóng lần lượt là
u1= 2cos( 20.t)mm và u2 = 2cos(20.t +)mm. Hai điểm M,N trên đoạn s1s2 có Ms1= 1cm; Ns2 =1,5cm. Biết tốc độ truyền sóng v = 20cm/s. Số điểm dao động với biên độ 4mm trên đoạn MN là:
A.11
B. 10
C. 12
D. 9
Câu 10:Hai nguồn kết hợp A và B dao động trên mặt nước theo các phương trình: u1 = 2cos(100pt + p/2) cm; u2 = 2cos(100pt) cm. Khi đó trên mặt nước, tạo ra một hệ thống vân giao thoa. Quan sát cho thấy, vân bậc k đi qua điểm P có hiệu số PA-PB = 5 cm và vân bậc k + 1 (cùng loại với vân k) đi qua điểm P’ có hiệu số P’A-P’B = 9 cm. Tìm Tốc độ truyền sóng trên mặt nước. Các vân nói trên là vân cực đại hay cực tiểu.
A.150cm/s;cực đại
B. 180cm/s;cực đại
C. 250cm/s;cực tiểu
D. 200cm/s;cực đại
Câu 11: Hai nguồn sóng kết hợp A và B cách nhau 19cm dao động ngược pha . Hai gơn hypecbol cùng loại thứ k và k+3 có hiệu đường đi lần lượt là 10cm và 22cm. Số điểm dao động cực đại trong khoảng AB là:
A. 10
B. 11
C. 12
D. 9
Câu 12: A,B là 2 nguồn kết hợp cùng pha trên mặt nước tạo hệ vân giao thoa. AB=5λ. Biên độ của mỗi nguồn là 5mm. Số điểm dao động với biên độ 5mm trên đường nối 2 nguồn là:
A. 20
B. 10
C. 24
D. 12
Câu 13: hai nguồn đồng bộ A,B cách nhau 50mm, ,v=0,8m/s, điểm gần nguồn nhất dđ cùng pha với nguồn nằm trên đường trung trực AB cách A một đoạn:
A: 32mm
B: 28mm
C: 34mm
D: 25mm
Câu 14: hai nguồn đồng bộ A,B cách nhau 11cm, ,v=0,4m/s, điểm gần nhất nguồn dđ ngược pha với nguồn nằm trên đường trung trực AB cách A một đoạn
:A: 8cm
B: 5,5cm
C: 4cm
D: 6cm
Câu 15: hai nguồn đồng bộ A,B cách nhau 14,5cm . Điểm M nằm trên đường trung trực AB gần A nhất dđ vuông pha với nguồn cách A một đoạn:
A: 9cm
B: 8,5cm
C: 4cm
D: 6cm
Câu 16: hai nguồn đồng bộ A,B cách nhau 8cm . Điêmt M nằm trên đường trung trực AB dđ cùng pha với nguồn cách AB một khoảng nhỏ nhất là:
A: 2cm
B: 2,8cm
C: 2,4cm
D: 3cm
Câu 17: hai nguồn đông bộ A,B cách nhau 16cm, f=25Hz, v=80cm/s. xét các điểm nằm trong vùng giao thoa trên đường thẳng vuông góc với AB tại B dđ với biên độ cực đại. điểm cách B gần nhất và xa nhất lần lượt là:
A: 39,6cm; 3,6cm
B: 80cm; 1,69cm
C: 38,4cm; 3,6cm
D: 79,2cm; 1,69cm
Trịnh Thị Thanh Link Download chính thức:
Đề thi học kì 2 Lớp 12 
Đề thi giữa học kì 1 Lớp 12 
Đề thi học kì 1 Lớp 12 
Soạn Văn 12 KNTT 
Soạn Văn 12 Cánh Diều 
Soạn Văn 12 CTST 
Văn 12 
Toán 12 Kết nối tri thức 
Toán 12 Cánh Diều 
Toán 12 Có thể bạn quan tâm
-
Giáo án Toán lớp 1 (Sách mới) - Giáo án Toán lớp 1 (trọn bộ 5 sách)
-
Tuyển tập đề thi học sinh giỏi môn Toán lớp 3
-
Thuyết minh về Thành Cổ Loa (2 Dàn ý + 5 mẫu)
-
Bộ tranh tô màu chủ đề gia đình cho bé
-
Văn mẫu lớp 10: Phân tích tác phẩm Hiền tài là nguyên khí của quốc gia (2 Dàn ý + 10 Mẫu)
-
Những vần thơ hay - Tuyển tập những bài thơ hay
-
Văn mẫu lớp 9: Nghị luận về hiện tượng học tủ, học vẹt
-
File luyện viết chữ in hoa - Mẫu chữ hoa cho học sinh Tiểu học
-
Đề kiểm tra học kì II môn Toán lớp 1
-
Văn mẫu lớp 7: Phân tích bài Ngẫu nhiên viết nhân buổi mới về quê
