Đề thi tuyển sinh lớp 10 THPT chuyên Trần Phú tỉnh Hải Phòng năm 2012 - 2013 môn Toán Đề thi tuyển sinh lớp 10

Câu I (2,0 điểm)

1) Cho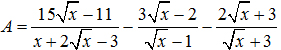

Rút gọn và tìm giá trị lớn nhất của A

2) Cho phương trình x² + ax + b = 0 có hai nghiệm nguyên dương biết a,b là hai số dương thỏa mãn 5a + b = 22.Tìm hai nghiệm đó.

Câu II (2,0 điểm)

1) Giải phương trình:

2) Giải hệ phương trình: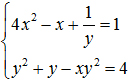

Câu III (1,0 điểm)

Cho ba số dương a, b, c. Chứng minh rằng:

Câu IV (2,0 điểm)

Cho tam giác ABC (AB < AC) có trực tâm H, nội tiếp đường tròn tâm O, đường kính AA’. Gọi AD là đường phân giác trong của góc. M, I lần lượt là trung điểm của BC và AH.

1) Lấy K đối xứng với H qua AD. Chứng minh K thuộc đường thẳng AA’.

2) Gọi P là giao điểm của AD với HM. Đường thẳng HK cắt AB và AC lần lượt tại Q và R. Chứng minh rằng Q và R lần lượt là hình chiếu vuông góc của P lên AB, AC.

Câu V (3,0 điểm)

1) Tìm nghiệm nguyên của phương trình x⁴ + y⁴ + z⁴ = 2012

2) Cho hình vuông 12x12, được chia thành lưới các hình vuông đơn vị. Mỗi đỉnh của hình vuông đơn vị này được tô bằng một trong hai màu xanh đỏ. Có tất cả 111 đỉnh màu đỏ. Hai trong số những đỉnh màu đỏ này nằm ở đỉnh hình vuông lớn, 22 đỉnh màu đỏ khác nằm trên cạnh cạnh của hình vuông lớn (không trùng với đỉnh của hình vuông lớn ) hình vuông đơn vị được tô màu theo các quy luật sau: cạnh có hai đầu mút màu đỏ được tô màu đỏ, cạnh có hai đầu mút màu xanh được tô màu xanh, cạnh có một đầu mút màu đỏ và một đầu mút màu xanh thì được tô màu vàng. Giả sứ có tất cả 66 cạnh vàng. Hỏi có bao nhiêu cạnh màu xanh.

Download tài liệu để xem thêm chi tiết.