Đề thi thử đại học năm 2014 trường THPT Nguyễn Đăng Đạo, Bắc Ninh Môn: Toán khối A, B, A1, V

Câu 1 (2 Điểm): Cho hàm số: y = x³ - m²x² - 3x + m (C_m)

a, Khảo sát sự biến thiên và vẽ đồ thị hàm số với m = 0

b, Gọi A là điểm trên (C_m) và có hoành độ bằng -1. Tìm m để tiếp tuyến của (C_m) tại A song song với đường thẳng d: y = 2x + 2.

Câu 2 (1 Điểm): Giải phương trình lượng giác:

sin2x - cos2x - 2 = sinx - 3cosx

Câu 3 (1 Điểm): Giải hệ phương trình: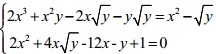

Câu 4 (1 Điểm): Tìm m để phương trình sau có đúng 1 nghiệm x < 1:

Câu 5 (1 Điểm):

Cho hình chóp S.ABCD, đáy ABCD là hình chữ nhật, AB = 2AD = 2a. Mặt bên SAB là tam giác vuông tại S và vuông góc với mặt phẳng (ABCD). Góc giữa SA với mặt phẳng (ABCD) bằng 60^o. Gọi M là trung điểm của SC. Tính thể tích khối chóp S.ABCD và khoảng cách giữa SB và DM.

Câu 6 (1 Điểm): Cho x, y, z là 3 số thực không âm thoả mãn:

Tìm giá trị lớn nhất của biểu thức: P = 2x³ + y³ + z³

Câu 7 (1 Điểm):

Trong mặt phẳng toạ độ Oxy, cho tam giác ABC có diện tích bằng 9/2. Các đỉnh A, B, C lần lượt nằm trên các đường thẳng d₁: x + y – 2 = 0; d₂: 2x – y – 4 = 0; d₃: x – y – 3 = 0. Gọi E, F là 2 điểm lần lượt nằm trên các cạnh AB và AC sao cho AB = 3AE; AC = 3CF. Đường thẳng EF cắt đường thẳng BC tại điểm P(-4; -8).

Tìm toạ độ các đỉnh của tam giác ABC.

Câu 8 (1 Điểm):

Trong mặt phẳng toạ độ Oxy, cho đường thẳng d: x – y = 0. Viết phương trình đường tròn (C) qua điểm M(2; 0) và tiếp xúc với d tại O(0;0).

Câu 9 (1 Điểm): Cho khai triển:

Biết rằng: a₀ + 2a₁ + 4a₂ + .... + 2ⁿa_n = 1024. Tìm a₆

Download tài liệu để xem chi tiết.