Đề thi học sinh giỏi Quốc gia lớp 12 THPT năm 2010 - môn Tin học Đề thi học sinh giỏi quốc gia
| BỘ GIÁO DỤC VÀ ĐÀO TẠO (Đề thi chính thức) |
KỲ THI CHỌN HỌC SINH GIỎI QUỐC GIA LỚP 12 THPT NĂM 2010 Môn: TIN HỌC Thời gian: 180 phút (không kể thời gian giao đề) Ngày thi: 11/03/2010 |
TỔNG QUAN BÀI THI
| Tên bài | File chương trình | File dữ liệu vào | File kết quả | |
| Bài 1 | Dãy con chung không liền kề dài nhất | LNACS.* | LANCS.INP | LNACS.OUT |
| Bài 2 | Ổn định | STABLE.* | STABLE.INP | STABLE.OUT |
| Bài 3 | Mã số thuế | TAXID.* | TAXID.INP | TAXID.OUT |
Dấu * được thay thế bởi PAS hoặc CPP của ngôn ngữ lập trình được sử dụng tương ứng là Pascal hoặc C++.
Hãy lập trình giải các bài toán sau:
Bài 1. Dãy con chung không liền kề dài nhất (6 điểm)
Dãy C = C1, C2, ..., Ck được gọi là dãy con không liền kề của dãy A = a1, a2,..., am nếu C có thể nhận được bằng cách chọn một dãy các phần tử không liền kề của A, nghĩa là tìm được dãy các chỉ số i1, i2, ..., ik sao cho:
i ≤ i1, i2, ..., ik ≤ m;
i1 < i2 - 1, i2 < i3 - 1, ..., ik-1 < ik - 1;
c1 = ai1, c2 = ai2, ..., ck = aik
Ta gọi độ dài của dãy là số phần tử của nó.
Cho hai dãy: A = a1, a2, ..., am và B = b1, b2, ..., bn
Dãy C được gọi là dãy con chung không liền kề của hai dãy A và B nếu như nó vừa là dãy con không liền kề của A, vừa là dãy con không liền kề của B.
Yêu cầu: Cho hai dãy số A và B. Hãy tìm độ dài của dãy con chung không liền kề dài nhất của hai dãy đã cho.
Dữ liệu: Vào từ file văn bản LNACS.INP:
- Dòng đầu tiên chứa hai số nguyên dương m và n (2 ≤ m, n ≤ 103) được ghi cách nhau bởi dấu cách, lần lượt là số lượng phần tử của dãy A và dãy B.
- Dòng thứ i trong m dòng tiếp theo chứa số nguyên không âm ai (ai ≤ 104), i = 1, 2, ..., m.
- Dòng thứ j trong n dòng tiếp theo chứa số nguyên không âm bj (bj ≤ 104), j = 1, 2, ..., m.
Kết quả: Ghi ra trên một dòng của file văn bản LNACS.OUT độ dài của dãy con chung không liền kề dài nhất của hai dãy A và B.
Bài 2. Ổn định (7 điểm)
Trong mạng xã hội, mỗi trang web được tổ chức trên một máy tính thành viên và cung cấp dịch vụ truy cập tới một số trang web khác. Để truy nhập tới một trang web nào đó không có trong danh mục kết nối trực tiếp của mình, người dùng phải truy nhập tới trang web khác có kết nối với mình, dựa vào danh mục dịch vụ của trang web này để chuyển tới trang web khác theo tùy chọn, cứ như thế cho đến khi tới được trang web mình cần. Thời gian để truy nhập tới một trang web phụ thuộc chủ yếu vào số lần mở trang web trong quá trình truy nhập. Như vậy, người dùng cần chủ động chọn lộ trình truy nhập hợp lý.
Sau một thời gian làm việc trên mạng, Sáng - một thành viên nhiệt thành đã tích lũy kinh nghiệm, tạo một cơ sở dữ liệu, cho biết từ một trang web có thể đi tới những trang web nào trong mạng. Trong cơ sở dữ liệu, các trang web được đánh số từ 1 đến n và có m bản ghi, mỗi bản ghi có dạng cặp có thứ tự (u, v) cho biết trang web u có thể kết nối tới trang web v (1 ≤ u, v ≤ n, u # v). Cơ sở dữ liệu chưa được chuẩn hóa, vì vậy có thể chứa các cặp (u, v) giống nhau.
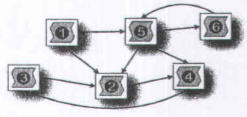
Trang web của Sáng có số hiệu là s. Dựa vào cơ sở dữ liệu, Sáng có thể xác định lộ trình truy nhập nhanh nhất (tức là số lần phải mở trang web là ít nhất) từ t rang web s tới trang web u bất kỳ. Tuy vậy, ở mạng xã hội, mọi chuyện đều có thể xảy ra: một khu vực nào đó bị mất điện, máy của một thành viên bị hỏng, trang web đang bị đóng để nâng cấp,... Kết quả là một vài trang web nào dó có thể tạm thời không hoạt động. Như vậy, nếu từ s có ít nhất hai lộ trình nhanh nhất khác nhau tới u thì khả năng thực hiện truy nhập được một cách nhanh nhất tới u là lớn hơn so với những trang web chỉ có duy nhất một lộ trình nhanh nhất. Hai lộ trình gọi là khác nhau nếu có ít nhất một trang web có ở lộ trình này mà không có ở lộ trình kia hoặc cả hai lộ trình cùng đi qua những trang web như nhau nhưng theo các trình tự khác nhau. Những trang web mà từ s tới đó có ít ra là hai lộ trình nhanh nhất khác nhau được gọi là ổn định đối với s. Trang web mà từ s không có lộ trình tới nó là không ổn định đối với s.
Ví dụ, với mạng nêu ở hình trên (n = 6, m = 9) các trang web 4 và 3 là ổn định đối với s = 1 (từ 1 tới 4 có 2 lộ trình nhanh nhất: 1-> 2 -> 4 và 1 -> 5 -> 4, từ 1 tới 3 cũng có 2 lộ trình nhanh nhất: 1 -> 2 -> 4 -> 3 và 1 -> 5 -> 4 -> 3)
Yêu cầu: Cho các số nguyên dương n, m, s và m cặp số (u, v) xác định từ u có thể kết nối trực tiếp tới được v. Hãy xác định số lượng trang web ổn định đối với s.
Dữ liệu: Vào từ file văn bản STABLE.INP:
- Dòng đầu tiên chứa 3 số nguyên n, m và s (2 ≤ n ≤ 10000, 1 ≤ m ≤ 50000, 1 ≤ s ≤ n).
- Mỗi dòng trong m dòng tiếp theo chứa 2 số nguyên u và v (1 ≤ u, v ≤ u, u # v).
Các số trên một dòng được ghi cách nhau ít nhất một dấu cách.
Kết quả: Đưa ra file văn bản STABLE.OUT một số nguyên - số trang web ổn định đối với s.
Bài 3: Mã số thuế (7 điểm)
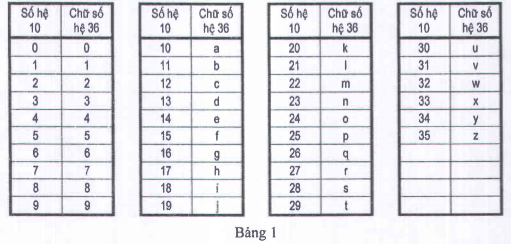
Để thực hiện luật Thuế thu nhập cá nhân, Tổng cục thuế phải cấp cho mỗi người có thu nhạp một mã số thuế sao cho không có hai người nào có mã số thuế trùng nhau. Tổng cục thuế quyết định chọn mã số thuế từ tập S bao gồm các biểu diễn trong hệ đếm cơ số 36 của tất cả các số nguyên dương trong phạm vi từ 1 đến n (36 ≤ n ≤1016). Để biểu diễn các chữ số trong hệ đếm cơ số 36, Tổng cục thuế sử dụng các ký tự từ 0 đến 9 và 26 chữ cái latinh từ a đến z theo quy tắc chỉ ra trong bảng 1. Một số trong hệ đếm cơ số 36 có thể hiểu là số biểu diễn trong hệ đếm cơ số q(2 ≤ 1 ≤ 36) nếu nó chỉ chứa các chữ số trong q chữ số đầu tiên trong hệ đếm cơ số 36.
Có tất cả m Cục thuế được đánh số từ 1 đến m làm nhiệm vụ duyệt hồ sơ và cấp mã số thuế (3 ≤ m ≤ 70). Để việc cấp mã số thuế có thể được tiến hành song song ở tất cả các Cục thuế, trước hết Tổng cục thuế chọn dãy số nguyên c1, c2, ..., ck thỏa mãn 1 < c1 < c2 <...<ck < 36, trong đó k = [(m-1)/2] (kí hiệu [α] là số nguyên lớn nhất bé hơn hoặc bằng α) và sau đó tiến hành phân phối mã số thuế cho các Cục thuế như sau: đầu tiên, từ tập S lọc ra tất cả các số có thể hiểu như là số trong hệ đếm cơ số c1 chuyển cho các Cục thuế thứ nhất và thứ hai sử dụng, sau đó loại bỏ tất cả các số này khỏi tập S; tiếp đến, lọc ra tất cả các số còn lại trong S có thể hiểu như số ở hệ đếm cơ số c2 chuyển cho các Cục thuế thứ 3 và thứ 4 sử dụng, sau đó loại bỏ tất cả các số này khỏi tập S;... Cục thuế cuối cùng (nếu m lẻ) hoặc 2 Cục thuế cuối cùng (nếu m chẵn) được sử dụng các mã còn lại trong tập S.
Yêu cầu: Cho ở dạng hệ đếm cơ số 10 các số nguyên dương n, m, c1, c2, ..., ck, p và q. Hãy xác định mã số thuế của người thứ q ở Cục thuế p.
Dữ liệu vào: Vào từ file văn bản TAXID.INP:
- Dòng thứ nhất chứa các số nguyên n, m, p, q.
- Dòng thứ hai chứa k số nguyên c1, c2, ..., ck (k = [(m-1)/2])
Các số trên cùng một dòng được ghi cách nhau một dấu cách. Dữ liệu đảm bảo tồn tại mã số thuế.
Kết quả: Đưa ra file văn bản TAXID.OUT mã số thuế tìm được.
Download tài liệu để xem thêm chi tiết
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:












 Đề thi học kì 1 Lớp 12
Đề thi học kì 1 Lớp 12
 Đề thi giữa học kì 1 Lớp 12
Đề thi giữa học kì 1 Lớp 12
 Đề thi giữa học kì 2 Lớp 12
Đề thi giữa học kì 2 Lớp 12
 Đề thi học kì 2 Lớp 12
Đề thi học kì 2 Lớp 12
 Soạn Văn 12 KNTT
Soạn Văn 12 KNTT
 Soạn Văn 12 CTST
Soạn Văn 12 CTST
 Soạn Văn 12 Cánh Diều
Soạn Văn 12 Cánh Diều
 Văn 12
Văn 12
 Toán 12 Chân trời sáng tạo
Toán 12 Chân trời sáng tạo









