Đề thi học sinh giỏi lớp 9 THCS tỉnh Tiền Giang năm 2012 - 2013 môn Toán - Có đáp án Sở GD-ĐT Tiền Giang

Tải về Bình luận

SỞ GIÁO DỤC VÀ ĐÀO TẠO
TIỀN GIANG

ĐỀ CHÍNH THỨC

KỲ THI CHỌN HSG LỚP 9 THCS CẤP TỈNH
Năm học: 2012 - 2013

MÔN THI: TOÁN
Thời gian làm bài: 150 phút (không kể thời gian giao đề)
Ngày thi: 20/03/2012

Câu 1: (4,0 điểm)

1. Giải hệ phương trình: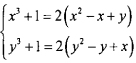

2. Cho phương trình x⁴ - 2mx² + 2m - 1 = 0 (1)

a. Tìm m để (1) có 4 nghiệm x₁, x₂, x₃, x₄ thỏa mãn:

b. Giải phương trình (1) với m vừa tìm được ở a.

Câu 2: (4,0 điểm)

Cho (P): y = x²; (d): y = x + m

Tìm m để (P) và (d) cắt nhau tại hai điểm phân biệt A, B sao cho: tam giác OAB là tam giác vuông

Câu 3: (4,0 điểm)

1. Cho 4 số a, b, c, d thỏa mãn điều kiện: a + b + c + d =

2. Chứng minh rằng: a² + b² + c² + d² ≥ 1

2. Cho m # -1 và a³ - 3a² + 3a(m + 1) - (m + 1)² = 0.

Hãy tìm giá trị nhỏ nhất (GTNN) của a.

Câu 4: (3,0 điểm)

Chứng minh rằng:

Câu 5: (5,0 điểm)

Cho tam giác ABC có các phân giác trong các góc nhọn BAC, ACB, CBA theo thứ tự cắt các cạnh đối tại các điểm M, P, N. Đặt a = BC, b = CA, c = AB; S_ΔMNP, S_ΔABC theo thứ tự là diện tích của tam giác MNP và tam giác ABC.

a. Chứng minh rằng:

b. Tìm giá trị lớn nhất (GTLN) của .

Download tài liệu để xem thêm chi tiết

Chia sẻ bởi:

Nguyễn Thu Ngân

Tải về

Liên kết tải về

Đề thi học sinh giỏi lớp 9 THCS tỉnh Tiền Giang năm 2012 - 2013 môn Toán - Có đáp án 106,1 KB Tải về

Tìm thêm: Toán 9

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!